Minimax Nonparametric Two-sample Test

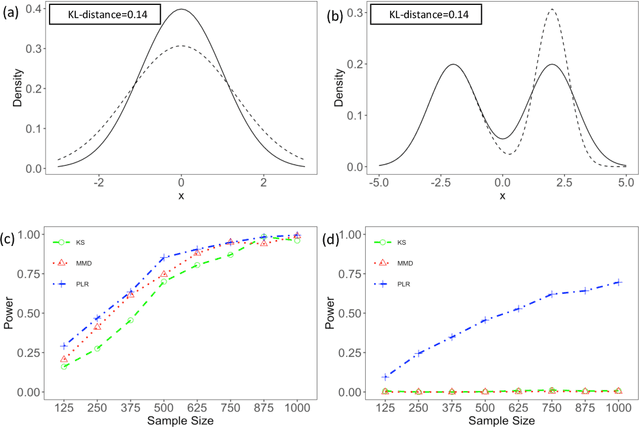
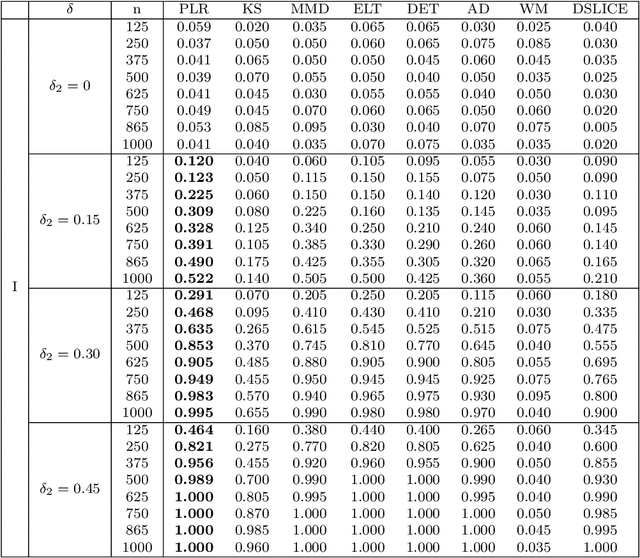
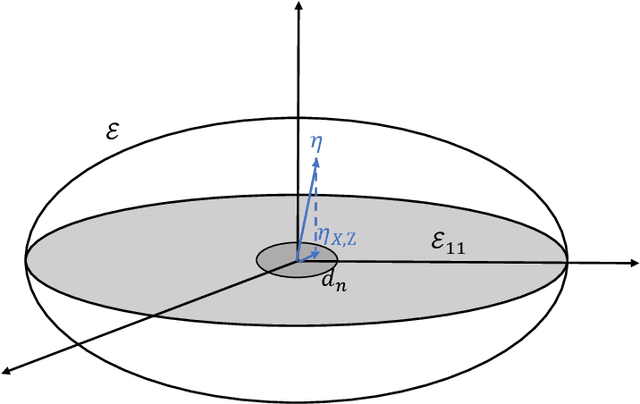
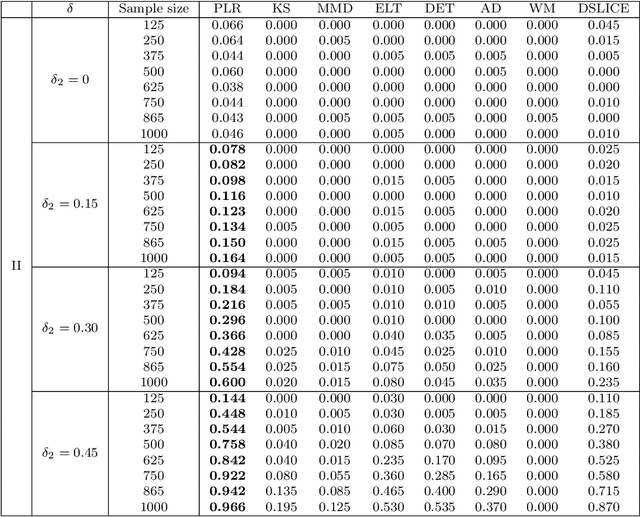
We consider the problem of comparing probability densities between two groups. To model the complex pattern of the underlying densities, we formulate the problem as a nonparametric density hypothesis testing problem. The major difficulty is that conventional tests may fail to distinguish the alternative from the null hypothesis under the controlled type I error. In this paper, we model log-transformed densities in a tensor product reproducing kernel Hilbert space (RKHS) and propose a probabilistic decomposition of this space. Under such a decomposition, we quantify the difference of the densities between two groups by the component norm in the probabilistic decomposition. Based on the Bernstein width, a sharp minimax lower bound of the distinguishable rate is established for the nonparametric two-sample test. We then propose a penalized likelihood ratio (PLR) test possessing the Wilks' phenomenon with an asymptotically Chi-square distributed test statistic and achieving the established minimax testing rate. Simulations and real applications demonstrate that the proposed test outperforms the conventional approaches under various scenarios.