Improving COVID-19 Forecasting using eXogenous Variables

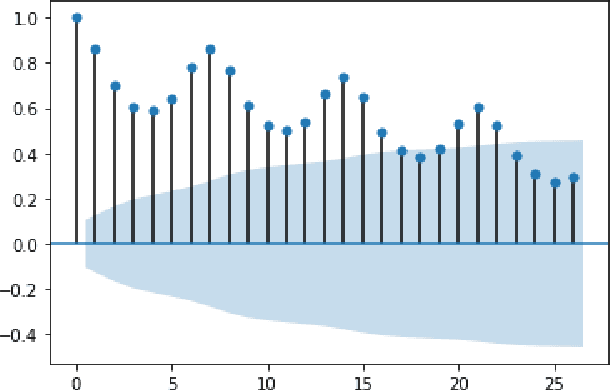
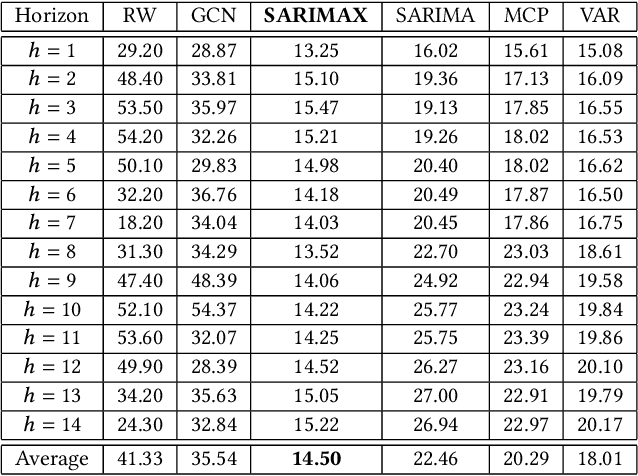
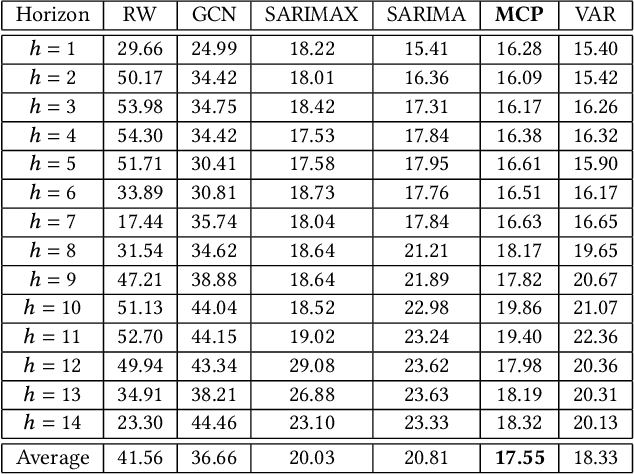
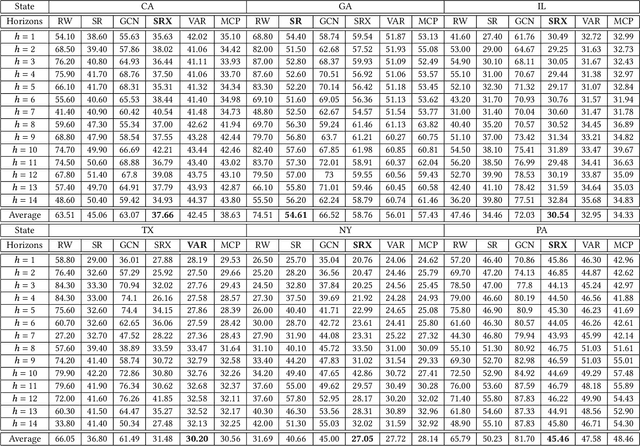
In this work, we study the pandemic course in the United States by considering national and state levels data. We propose and compare multiple time-series prediction techniques which incorporate auxiliary variables. One type of approach is based on spatio-temporal graph neural networks which forecast the pandemic course by utilizing a hybrid deep learning architecture and human mobility data. Nodes in this graph represent the state-level deaths due to COVID-19, edges represent the human mobility trend and temporal edges correspond to node attributes across time. The second approach is based on a statistical technique for COVID-19 mortality prediction in the United States that uses the SARIMA model and eXogenous variables. We evaluate these techniques on both state and national levels COVID-19 data in the United States and claim that the SARIMA and MCP models generated forecast values by the eXogenous variables can enrich the underlying model to capture complexity in respectively national and state levels data. We demonstrate significant enhancement in the forecasting accuracy for a COVID-19 dataset, with a maximum improvement in forecasting accuracy by 64.58% and 59.18% (on average) over the GCN-LSTM model in the national level data, and 58.79% and 52.40% (on average) over the GCN-LSTM model in the state level data. Additionally, our proposed model outperforms a parallel study (AUG-NN) by 27.35% improvement of accuracy on average.

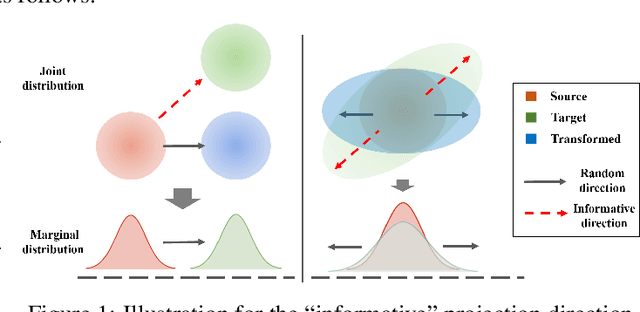
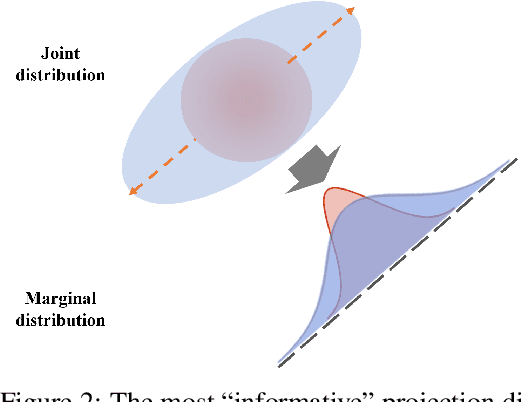
Large-scale optimal transport map estimation using projection pursuit

This paper studies the estimation of large-scale optimal transport maps (OTM), which is a well-known challenging problem owing to the curse of dimensionality. Existing literature approximates the large-scale OTM by a series of one-dimensional OTM problems through iterative random projection. Such methods, however, suffer from slow or none convergence in practice due to the nature of randomly selected projection directions. Instead, we propose an estimation method of large-scale OTM by combining the idea of projection pursuit regression and sufficient dimension reduction. The proposed method, named projection pursuit Monge map (PPMM), adaptively selects the most ``informative'' projection direction in each iteration. We theoretically show the proposed dimension reduction method can consistently estimate the most ``informative'' projection direction in each iteration. Furthermore, the PPMM algorithm weakly convergences to the target large-scale OTM in a reasonable number of steps. Empirically, PPMM is computationally easy and converges fast. We assess its finite sample performance through the applications of Wasserstein distance estimation and generative models.

Model-free Feature Screening and FDR Control with Knockoff Features

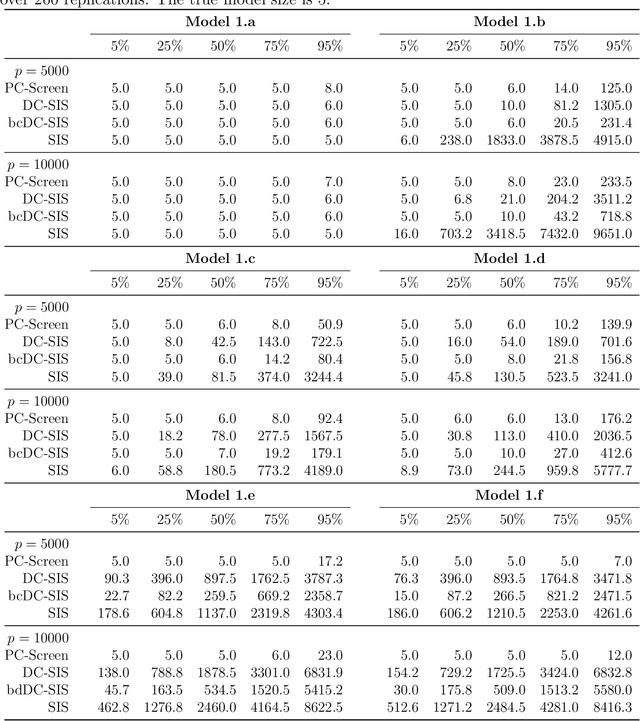
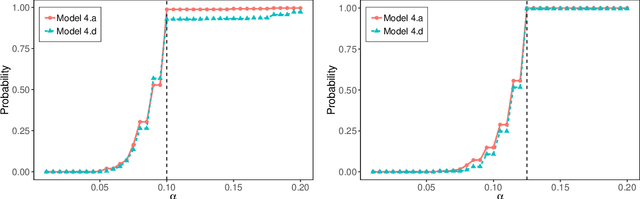
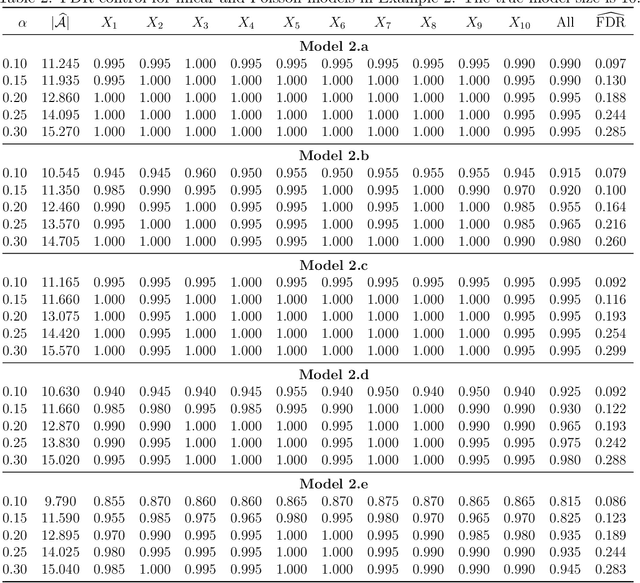
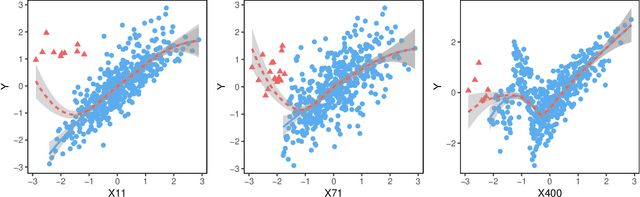
This paper proposes a model-free and data-adaptive feature screening method for ultra-high dimensional datasets. The proposed method is based on the projection correlation which measures the dependence between two random vectors. This projection correlation based method does not require specifying a regression model and applies to the data in the presence of heavy-tailed errors and multivariate response. It enjoys both sure screening and rank consistency properties under weak assumptions. Further, a two-step approach is proposed to control the false discovery rate (FDR) in feature screening with the help of knockoff features. It can be shown that the proposed two-step approach enjoys both sure screening and FDR control if the pre-specified FDR level $\alpha$ is greater or equal to $1/s$, where $s$ is the number of active features. The superior empirical performance of the proposed methods is justified by various numerical experiments and real data applications.