Generalized Causal Tree for Uplift Modeling

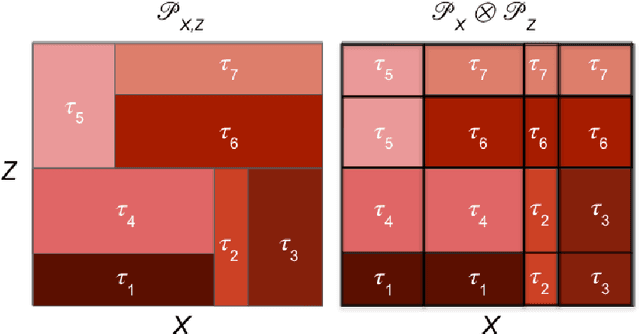
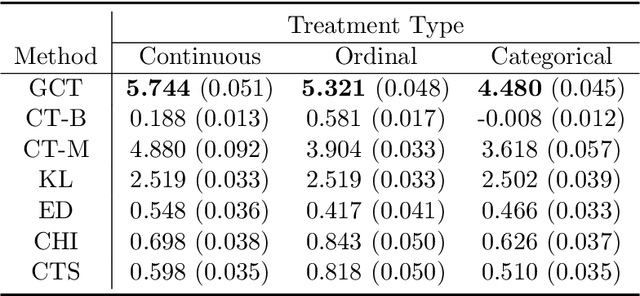
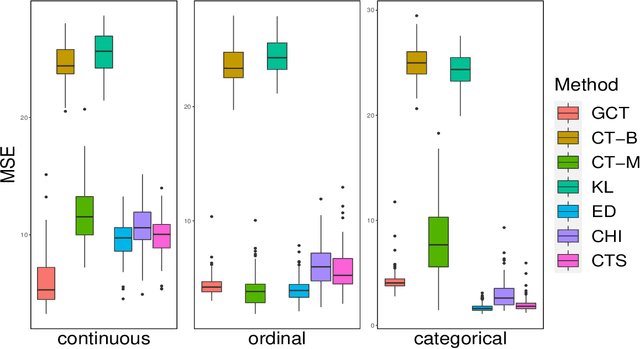
Uplift modeling is crucial in various applications ranging from marketing and policy-making to personalized recommendations. The main objective is to learn optimal treatment allocations for a heterogeneous population. A primary line of existing work modifies the loss function of the decision tree algorithm to identify cohorts with heterogeneous treatment effects. Another line of work estimates the individual treatment effects separately for the treatment group and the control group using off-the-shelf supervised learning algorithms. The former approach that directly models the heterogeneous treatment effect is known to outperform the latter in practice. However, the existing tree-based methods are mostly limited to a single treatment and a single control use case, except for a handful of extensions to multiple discrete treatments. In this paper, we fill this gap in the literature by proposing a generalization to the tree-based approaches to tackle multiple discrete and continuous-valued treatments. We focus on a generalization of the well-known causal tree algorithm due to its desirable statistical properties, but our generalization technique can be applied to other tree-based approaches as well. We perform extensive experiments to showcase the efficacy of our method when compared to other methods.

Model-free Feature Screening and FDR Control with Knockoff Features

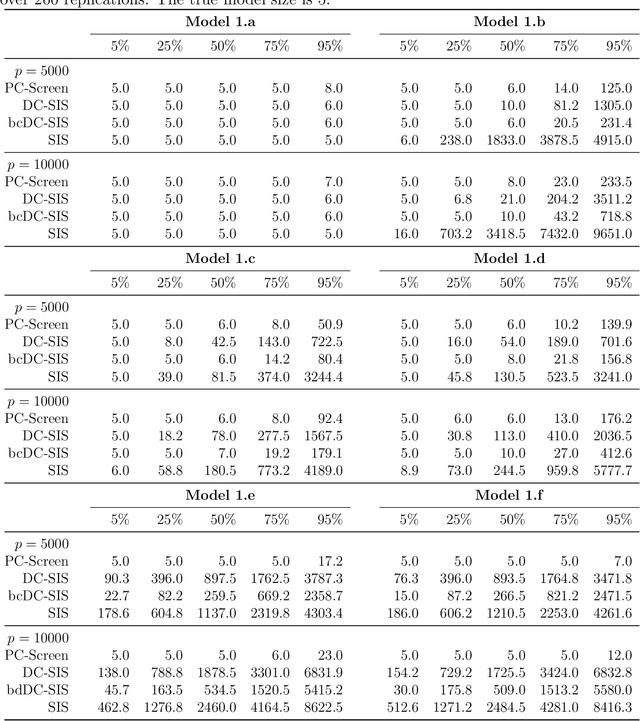
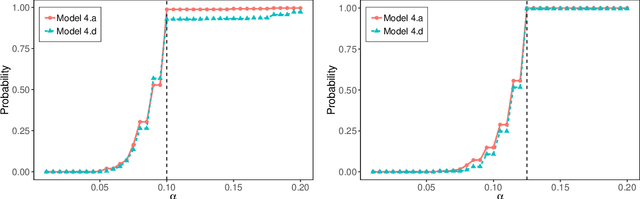
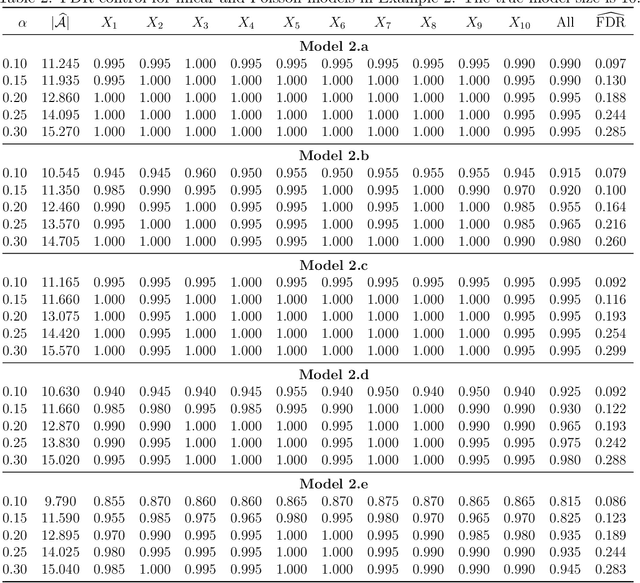
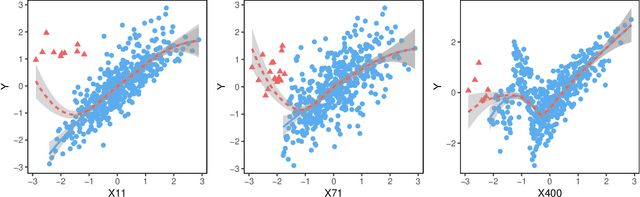
This paper proposes a model-free and data-adaptive feature screening method for ultra-high dimensional datasets. The proposed method is based on the projection correlation which measures the dependence between two random vectors. This projection correlation based method does not require specifying a regression model and applies to the data in the presence of heavy-tailed errors and multivariate response. It enjoys both sure screening and rank consistency properties under weak assumptions. Further, a two-step approach is proposed to control the false discovery rate (FDR) in feature screening with the help of knockoff features. It can be shown that the proposed two-step approach enjoys both sure screening and FDR control if the pre-specified FDR level $\alpha$ is greater or equal to $1/s$, where $s$ is the number of active features. The superior empirical performance of the proposed methods is justified by various numerical experiments and real data applications.