Analysis of Multiscale Reinforcement Q-Learning Algorithms for Mean Field Control Games

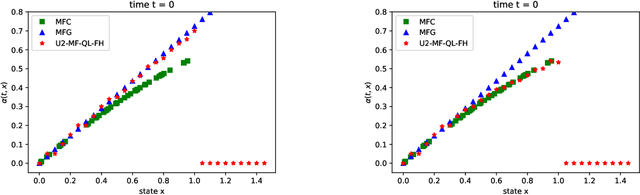
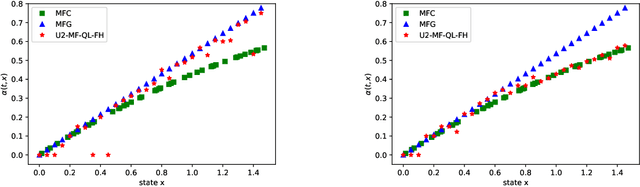
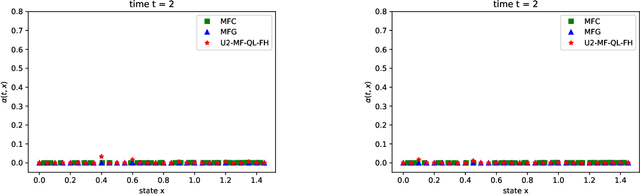
Mean Field Control Games (MFCG), introduced in [Angiuli et al., 2022a], represent competitive games between a large number of large collaborative groups of agents in the infinite limit of number and size of groups. In this paper, we prove the convergence of a three-timescale Reinforcement Q-Learning (RL) algorithm to solve MFCG in a model-free approach from the point of view of representative agents. Our analysis uses a Q-table for finite state and action spaces updated at each discrete time-step over an infinite horizon. In [Angiuli et al., 2023], we proved convergence of two-timescale algorithms for MFG and MFC separately highlighting the need to follow multiple population distributions in the MFC case. Here, we integrate this feature for MFCG as well as three rates of update decreasing to zero in the proper ratios. Our technique of proof uses a generalization to three timescales of the two-timescale analysis in [Borkar, 1997]. We give a simple example satisfying the various hypothesis made in the proof of convergence and illustrating the performance of the algorithm.

Deep Reinforcement Learning for Infinite Horizon Mean Field Problems in Continuous Spaces

We present the development and analysis of a reinforcement learning (RL) algorithm designed to solve continuous-space mean field game (MFG) and mean field control (MFC) problems in a unified manner. The proposed approach pairs the actor-critic (AC) paradigm with a representation of the mean field distribution via a parameterized score function, which can be efficiently updated in an online fashion, and uses Langevin dynamics to obtain samples from the resulting distribution. The AC agent and the score function are updated iteratively to converge, either to the MFG equilibrium or the MFC optimum for a given mean field problem, depending on the choice of learning rates. A straightforward modification of the algorithm allows us to solve mixed mean field control games (MFCGs). The performance of our algorithm is evaluated using linear-quadratic benchmarks in the asymptotic infinite horizon framework.

Deep Learning for Systemic Risk Measures

The aim of this paper is to study a new methodological framework for systemic risk measures by applying deep learning method as a tool to compute the optimal strategy of capital allocations. Under this new framework, systemic risk measures can be interpreted as the minimal amount of cash that secures the aggregated system by allocating capital to the single institutions before aggregating the individual risks. This problem has no explicit solution except in very limited situations. Deep learning is increasingly receiving attention in financial modelings and risk management and we propose our deep learning based algorithms to solve both the primal and dual problems of the risk measures, and thus to learn the fair risk allocations. In particular, our method for the dual problem involves the training philosophy inspired by the well-known Generative Adversarial Networks (GAN) approach and a newly designed direct estimation of Radon-Nikodym derivative. We close the paper with substantial numerical studies of the subject and provide interpretations of the risk allocations associated to the systemic risk measures. In the particular case of exponential preferences, numerical experiments demonstrate excellent performance of the proposed algorithm, when compared with the optimal explicit solution as a benchmark.

Reinforcement Learning for Mean Field Games, with Applications to Economics

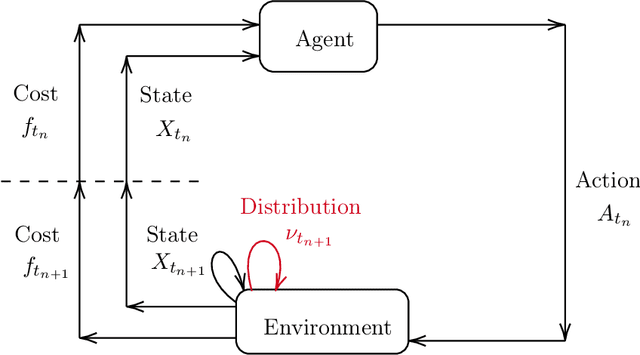
Mean field games (MFG) and mean field control problems (MFC) are frameworks to study Nash equilibria or social optima in games with a continuum of agents. These problems can be used to approximate competitive or cooperative games with a large finite number of agents and have found a broad range of applications, in particular in economics. In recent years, the question of learning in MFG and MFC has garnered interest, both as a way to compute solutions and as a way to model how large populations of learners converge to an equilibrium. Of particular interest is the setting where the agents do not know the model, which leads to the development of reinforcement learning (RL) methods. After reviewing the literature on this topic, we present a two timescale approach with RL for MFG and MFC, which relies on a unified Q-learning algorithm. The main novelty of this method is to simultaneously update an action-value function and a distribution but with different rates, in a model-free fashion. Depending on the ratio of the two learning rates, the algorithm learns either the MFG or the MFC solution. To illustrate this method, we apply it to a mean field problem of accumulated consumption in finite horizon with HARA utility function, and to a trader's optimal liquidation problem.

Unified Reinforcement Q-Learning for Mean Field Game and Control Problems

We present a Reinforcement Learning (RL) algorithm to solve infinite horizon asymptotic Mean Field Game (MFG) and Mean Field Control (MFC) problems. Our approach can be described as a unified two-timescale Mean Field Q-learning: The same algorithm can learn either the MFG or the MFC solution by simply tuning a parameter. The algorithm is in discrete time and space where the agent not only provides an action to the environment but also a distribution of the state in order to take into account the mean field feature of the problem. Importantly, we assume that the agent can not observe the population's distribution and needs to estimate it in a model-free manner. The asymptotic MFG and MFC problems are presented in continuous time and space, and compared with classical (non-asymptotic or stationary) MFG and MFC problems. They lead to explicit solutions in the linear-quadratic (LQ) case that are used as benchmarks for the results of our algorithm.