Directed Chain Generative Adversarial Networks

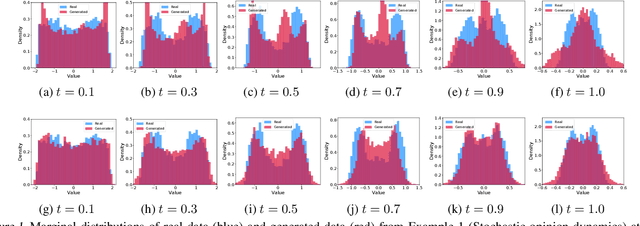
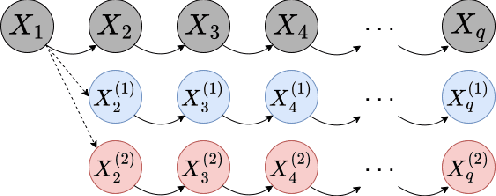
Real-world data can be multimodal distributed, e.g., data describing the opinion divergence in a community, the interspike interval distribution of neurons, and the oscillators natural frequencies. Generating multimodal distributed real-world data has become a challenge to existing generative adversarial networks (GANs). For example, neural stochastic differential equations (Neural SDEs), treated as infinite-dimensional GANs, have demonstrated successful performance mainly in generating unimodal time series data. In this paper, we propose a novel time series generator, named directed chain GANs (DC-GANs), which inserts a time series dataset (called a neighborhood process of the directed chain or input) into the drift and diffusion coefficients of the directed chain SDEs with distributional constraints. DC-GANs can generate new time series of the same distribution as the neighborhood process, and the neighborhood process will provide the key step in learning and generating multimodal distributed time series. The proposed DC-GANs are examined on four datasets, including two stochastic models from social sciences and computational neuroscience, and two real-world datasets on stock prices and energy consumption. To our best knowledge, DC-GANs are the first work that can generate multimodal time series data and consistently outperforms state-of-the-art benchmarks with respect to measures of distribution, data similarity, and predictive ability.

Deep Learning for Systemic Risk Measures

The aim of this paper is to study a new methodological framework for systemic risk measures by applying deep learning method as a tool to compute the optimal strategy of capital allocations. Under this new framework, systemic risk measures can be interpreted as the minimal amount of cash that secures the aggregated system by allocating capital to the single institutions before aggregating the individual risks. This problem has no explicit solution except in very limited situations. Deep learning is increasingly receiving attention in financial modelings and risk management and we propose our deep learning based algorithms to solve both the primal and dual problems of the risk measures, and thus to learn the fair risk allocations. In particular, our method for the dual problem involves the training philosophy inspired by the well-known Generative Adversarial Networks (GAN) approach and a newly designed direct estimation of Radon-Nikodym derivative. We close the paper with substantial numerical studies of the subject and provide interpretations of the risk allocations associated to the systemic risk measures. In the particular case of exponential preferences, numerical experiments demonstrate excellent performance of the proposed algorithm, when compared with the optimal explicit solution as a benchmark.

Sample-Efficient Reinforcement Learning with loglog Switching Cost

We study the problem of reinforcement learning (RL) with low (policy) switching cost - a problem well-motivated by real-life RL applications in which deployments of new policies are costly and the number of policy updates must be low. In this paper, we propose a new algorithm based on stage-wise exploration and adaptive policy elimination that achieves a regret of $\widetilde{O}(\sqrt{H^4S^2AT})$ while requiring a switching cost of $O(HSA \log\log T)$. This is an exponential improvement over the best-known switching cost $O(H^2SA\log T)$ among existing methods with $\widetilde{O}(\mathrm{poly}(H,S,A)\sqrt{T})$ regret. In the above, $S,A$ denotes the number of states and actions in an $H$-horizon episodic Markov Decision Process model with unknown transitions, and $T$ is the number of steps. We also prove an information-theoretical lower bound which says that a switching cost of $\Omega(HSA)$ is required for any no-regret algorithm. As a byproduct, our new algorithmic techniques allow us to derive a \emph{reward-free} exploration algorithm with an optimal switching cost of $O(HSA)$.

Signatured Deep Fictitious Play for Mean Field Games with Common Noise

Existing deep learning methods for solving mean-field games (MFGs) with common noise fix the sampling common noise paths and then solve the corresponding MFGs. This leads to a nested-loop structure with millions of simulations of common noise paths in order to produce accurate solutions, which results in prohibitive computational cost and limits the applications to a large extent. In this paper, based on the rough path theory, we propose a novel single-loop algorithm, named signatured deep fictitious play, by which we can work with the unfixed common noise setup to avoid the nested-loop structure and reduce the computational complexity significantly. The proposed algorithm can accurately capture the effect of common uncertainty changes on mean-field equilibria without further training of neural networks, as previously needed in the existing machine learning algorithms. The efficiency is supported by three applications, including linear-quadratic MFGs, mean-field portfolio game, and mean-field game of optimal consumption and investment. Overall, we provide a new point of view from the rough path theory to solve MFGs with common noise with significantly improved efficiency and an extensive range of applications. In addition, we report the first deep learning work to deal with extended MFGs (a mean-field interaction via both the states and controls) with common noise.

Convolutional Signature for Sequential Data

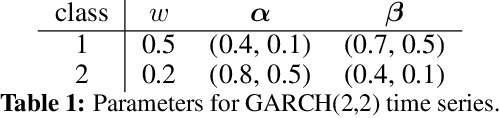
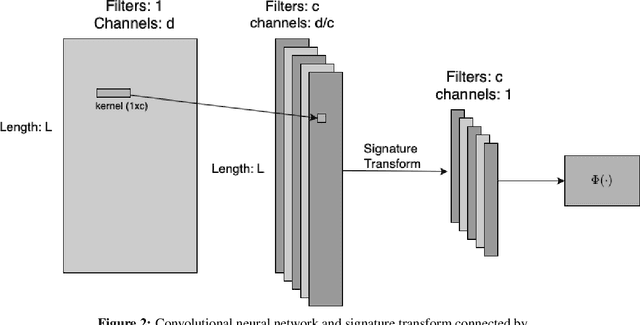
Signature is an infinite graded sequence of statistics known to characterize geometric rough paths, which includes the paths with bounded variation. This object has been studied successfully for machine learning with mostly applications in low dimensional cases. In the high dimensional case, it suffers from exponential growth in the number of features in truncated signature transform. We propose a novel neural network based model which borrows the idea from Convolutional Neural Network to address this problem. Our model reduces the number of features efficiently in a data dependent way. Some empirical experiments are provided to support our model.