A Deep Learning Analysis of Climate Change, Innovation, and Uncertainty

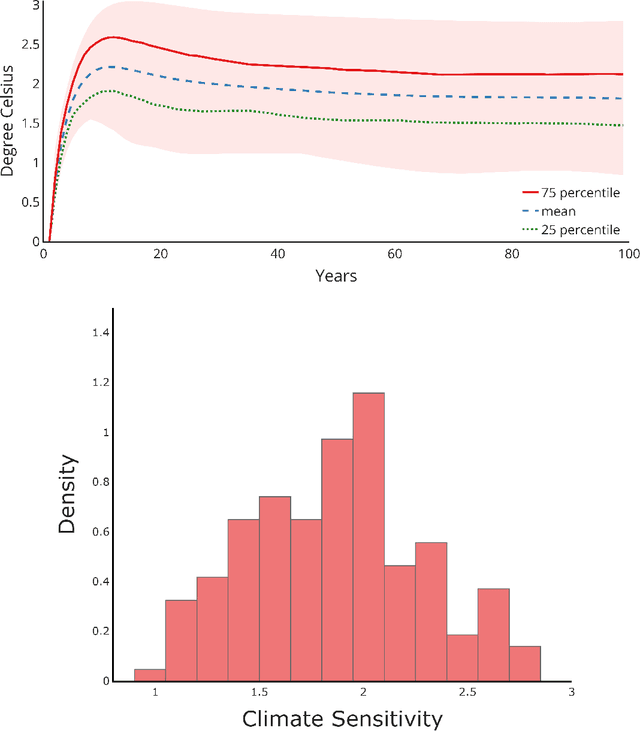
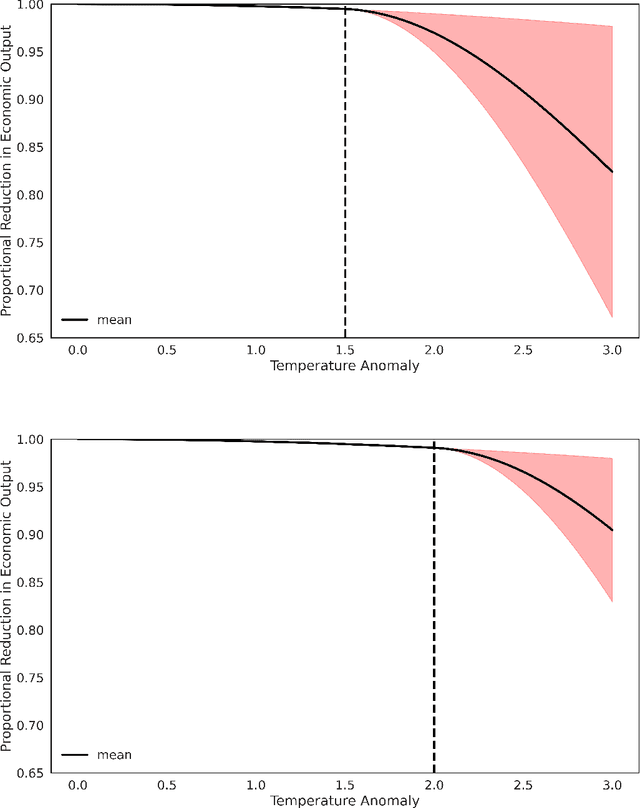
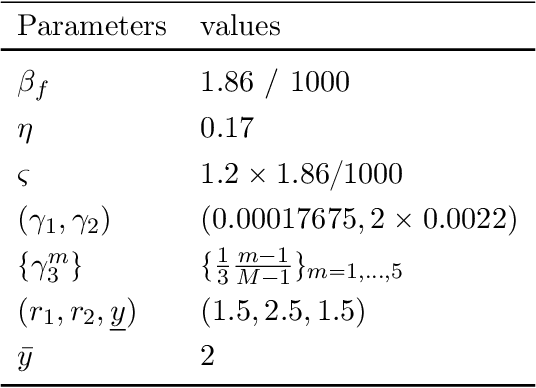
We study the implications of model uncertainty in a climate-economics framework with three types of capital: "dirty" capital that produces carbon emissions when used for production, "clean" capital that generates no emissions but is initially less productive than dirty capital, and knowledge capital that increases with R\&D investment and leads to technological innovation in green sector productivity. To solve our high-dimensional, non-linear model framework we implement a neural-network-based global solution method. We show there are first-order impacts of model uncertainty on optimal decisions and social valuations in our integrated climate-economic-innovation framework. Accounting for interconnected uncertainty over climate dynamics, economic damages from climate change, and the arrival of a green technological change leads to substantial adjustments to investment in the different capital types in anticipation of technological change and the revelation of climate damage severity.

Deep Reinforcement Learning for Infinite Horizon Mean Field Problems in Continuous Spaces

We present the development and analysis of a reinforcement learning (RL) algorithm designed to solve continuous-space mean field game (MFG) and mean field control (MFC) problems in a unified manner. The proposed approach pairs the actor-critic (AC) paradigm with a representation of the mean field distribution via a parameterized score function, which can be efficiently updated in an online fashion, and uses Langevin dynamics to obtain samples from the resulting distribution. The AC agent and the score function are updated iteratively to converge, either to the MFG equilibrium or the MFC optimum for a given mean field problem, depending on the choice of learning rates. A straightforward modification of the algorithm allows us to solve mixed mean field control games (MFCGs). The performance of our algorithm is evaluated using linear-quadratic benchmarks in the asymptotic infinite horizon framework.

Stochastic Delay Differential Games: Financial Modeling and Machine Learning Algorithms

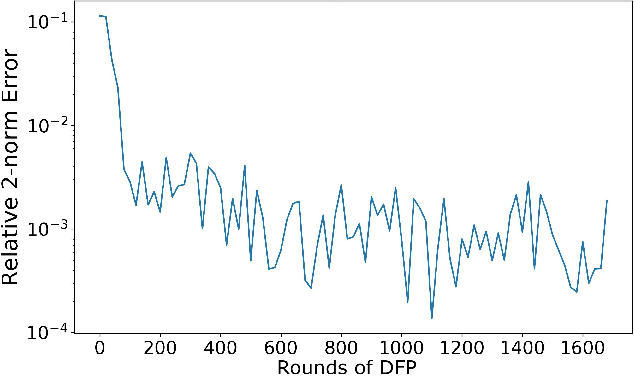
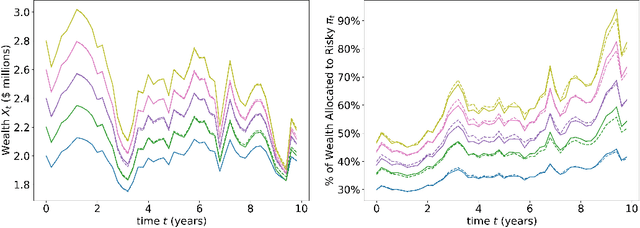
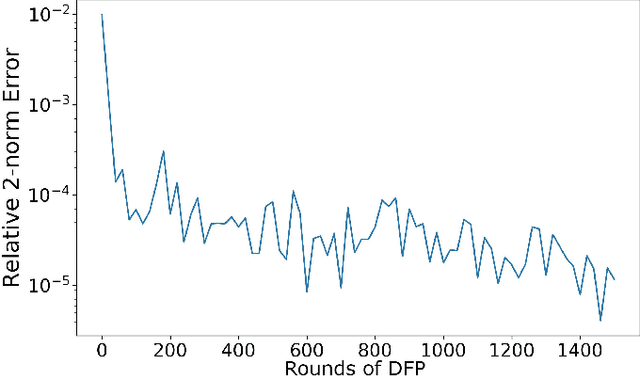
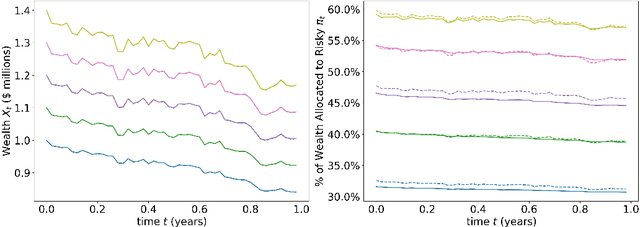
In this paper, we propose a numerical methodology for finding the closed-loop Nash equilibrium of stochastic delay differential games through deep learning. These games are prevalent in finance and economics where multi-agent interaction and delayed effects are often desired features in a model, but are introduced at the expense of increased dimensionality of the problem. This increased dimensionality is especially significant as that arising from the number of players is coupled with the potential infinite dimensionality caused by the delay. Our approach involves parameterizing the controls of each player using distinct recurrent neural networks. These recurrent neural network-based controls are then trained using a modified version of Brown's fictitious play, incorporating deep learning techniques. To evaluate the effectiveness of our methodology, we test it on finance-related problems with known solutions. Furthermore, we also develop new problems and derive their analytical Nash equilibrium solutions, which serve as additional benchmarks for assessing the performance of our proposed deep learning approach.

Directed Chain Generative Adversarial Networks

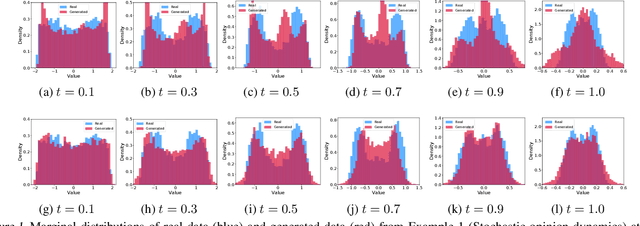
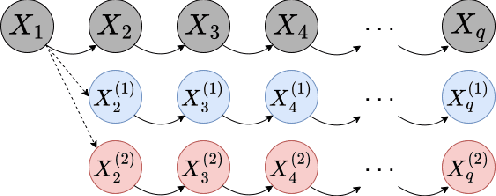
Real-world data can be multimodal distributed, e.g., data describing the opinion divergence in a community, the interspike interval distribution of neurons, and the oscillators natural frequencies. Generating multimodal distributed real-world data has become a challenge to existing generative adversarial networks (GANs). For example, neural stochastic differential equations (Neural SDEs), treated as infinite-dimensional GANs, have demonstrated successful performance mainly in generating unimodal time series data. In this paper, we propose a novel time series generator, named directed chain GANs (DC-GANs), which inserts a time series dataset (called a neighborhood process of the directed chain or input) into the drift and diffusion coefficients of the directed chain SDEs with distributional constraints. DC-GANs can generate new time series of the same distribution as the neighborhood process, and the neighborhood process will provide the key step in learning and generating multimodal distributed time series. The proposed DC-GANs are examined on four datasets, including two stochastic models from social sciences and computational neuroscience, and two real-world datasets on stock prices and energy consumption. To our best knowledge, DC-GANs are the first work that can generate multimodal time series data and consistently outperforms state-of-the-art benchmarks with respect to measures of distribution, data similarity, and predictive ability.

Recent Developments in Machine Learning Methods for Stochastic Control and Games

Stochastic optimal control and games have found a wide range of applications, from finance and economics to social sciences, robotics and energy management. Many real-world applications involve complex models which have driven the development of sophisticated numerical methods. Recently, computational methods based on machine learning have been developed for stochastic control problems and games. We review such methods, with a focus on deep learning algorithms that have unlocked the possibility to solve such problems even when the dimension is high or when the structure is very complex, beyond what is feasible with traditional numerical methods. Here, we consider mostly the continuous time and continuous space setting. Many of the new approaches build on recent neural-network based methods for high-dimensional partial differential equations or backward stochastic differential equations, or on model-free reinforcement learning for Markov decision processes that have led to breakthrough results. In this paper we provide an introduction to these methods and summarize state-of-the-art works on machine learning for stochastic control and games.

Convergence of the Backward Deep BSDE Method with Applications to Optimal Stopping Problems

The optimal stopping problem is one of the core problems in financial markets, with broad applications such as pricing American and Bermudan options. The deep BSDE method [Han, Jentzen and E, PNAS, 115(34):8505-8510, 2018] has shown great power in solving high-dimensional forward-backward stochastic differential equations (FBSDEs), and inspired many applications. However, the method solves backward stochastic differential equations (BSDEs) in a forward manner, which can not be used for optimal stopping problems that in general require running BSDE backwardly. To overcome this difficulty, a recent paper [Wang, Chen, Sudjianto, Liu and Shen, arXiv:1807.06622, 2018] proposed the backward deep BSDE method to solve the optimal stopping problem. In this paper, we provide the rigorous theory for the backward deep BSDE method. Specifically, 1. We derive the a posteriori error estimation, i.e., the error of the numerical solution can be bounded by the training loss function; and; 2. We give an upper bound of the loss function, which can be sufficiently small subject to universal approximations. We give two numerical examples, which present consistent performance with the proved theory.

Pandemic Control, Game Theory and Machine Learning

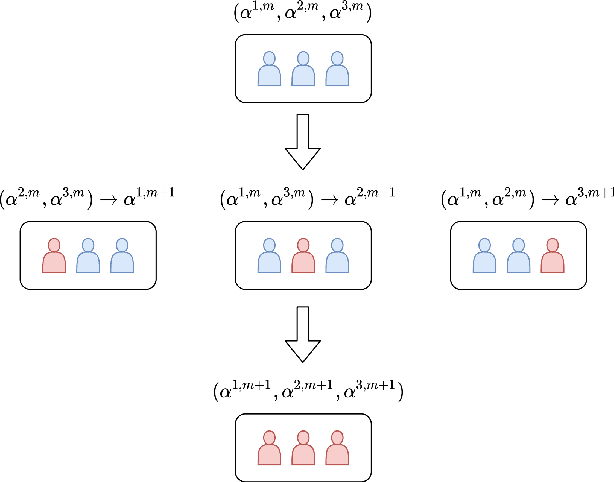
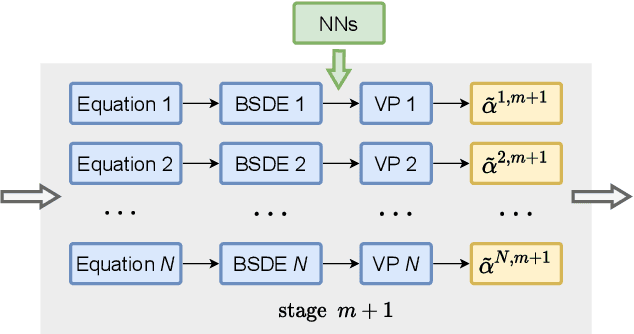
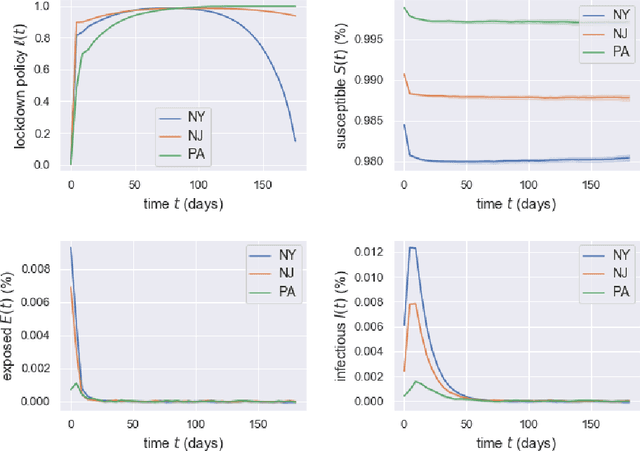
Game theory has been an effective tool in the control of disease spread and in suggesting optimal policies at both individual and area levels. In this AMS Notices article, we focus on the decision-making development for the intervention of COVID-19, aiming to provide mathematical models and efficient machine learning methods, and justifications for related policies that have been implemented in the past and explain how the authorities' decisions affect their neighboring regions from a game theory viewpoint.

Learning High-Dimensional McKean-Vlasov Forward-Backward Stochastic Differential Equations with General Distribution Dependence

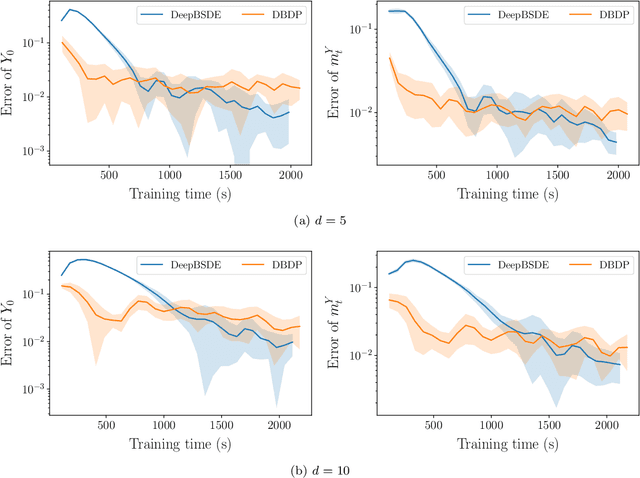
One of the core problems in mean-field control and mean-field games is to solve the corresponding McKean-Vlasov forward-backward stochastic differential equations (MV-FBSDEs). Most existing methods are tailored to special cases in which the mean-field interaction only depends on expectation or other moments and thus inadequate to solve problems when the mean-field interaction has full distribution dependence. In this paper, we propose a novel deep learning method for computing MV-FBSDEs with a general form of mean-field interactions. Specifically, built on fictitious play, we recast the problem into repeatedly solving standard FBSDEs with explicit coefficient functions. These coefficient functions are used to approximate the MV-FBSDEs' model coefficients with full distribution dependence, and are updated by solving another supervising learning problem using training data simulated from the last iteration's FBSDE solutions. We use deep neural networks to solve standard BSDEs and approximate coefficient functions in order to solve high-dimensional MV-FBSDEs. Under proper assumptions on the learned functions, we prove that the convergence of the proposed method is free of the curse of dimensionality (CoD) by using the generalized maximum mean discrepancy metric previously developed in [Han, Hu and Long, arXiv:2104.12036]. The proved theorem shows the advantage of the method in high dimensions. We present the numerical performance in high-dimensional MV-FBSDE problems, including a mean-field game example of the well-known Cucker-Smale model whose cost depends on the full distribution of the forward process.

Signatured Deep Fictitious Play for Mean Field Games with Common Noise

Existing deep learning methods for solving mean-field games (MFGs) with common noise fix the sampling common noise paths and then solve the corresponding MFGs. This leads to a nested-loop structure with millions of simulations of common noise paths in order to produce accurate solutions, which results in prohibitive computational cost and limits the applications to a large extent. In this paper, based on the rough path theory, we propose a novel single-loop algorithm, named signatured deep fictitious play, by which we can work with the unfixed common noise setup to avoid the nested-loop structure and reduce the computational complexity significantly. The proposed algorithm can accurately capture the effect of common uncertainty changes on mean-field equilibria without further training of neural networks, as previously needed in the existing machine learning algorithms. The efficiency is supported by three applications, including linear-quadratic MFGs, mean-field portfolio game, and mean-field game of optimal consumption and investment. Overall, we provide a new point of view from the rough path theory to solve MFGs with common noise with significantly improved efficiency and an extensive range of applications. In addition, we report the first deep learning work to deal with extended MFGs (a mean-field interaction via both the states and controls) with common noise.

A Class of Dimensionality-free Metrics for the Convergence of Empirical Measures

This paper concerns the convergence of empirical measures in high dimensions. We propose a new class of metrics and show that under such metrics, the convergence is free of the curse of dimensionality (CoD). Such a feature is critical for high-dimensional analysis and stands in contrast to classical metrics ({\it e.g.}, the Wasserstein distance). The proposed metrics originate from the maximum mean discrepancy, which we generalize by proposing specific criteria for selecting test function spaces to guarantee the property of being free of CoD. Therefore, we call this class of metrics the generalized maximum mean discrepancy (GMMD). Examples of the selected test function spaces include the reproducing kernel Hilbert space, Barron space, and flow-induced function spaces. Three applications of the proposed metrics are presented: 1. The convergence of empirical measure in the case of random variables; 2. The convergence of $n$-particle system to the solution to McKean-Vlasov stochastic differential equation; 3. The construction of an $\varepsilon$-Nash equilibrium for a homogeneous $n$-player game by its mean-field limit. As a byproduct, we prove that, given a distribution close to the target distribution measured by GMMD and a certain representation of the target distribution, we can generate a distribution close to the target one in terms of the Wasserstein distance and relative entropy. Overall, we show that the proposed class of metrics is a powerful tool to analyze the convergence of empirical measures in high dimensions without CoD.