Hector D. Ceniceros
Stochastic Delay Differential Games: Financial Modeling and Machine Learning Algorithms
Jul 12, 2023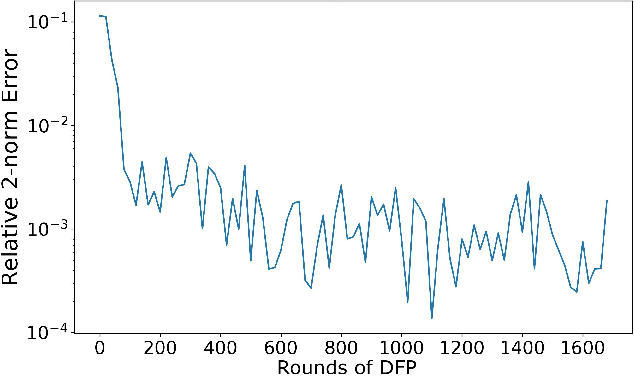
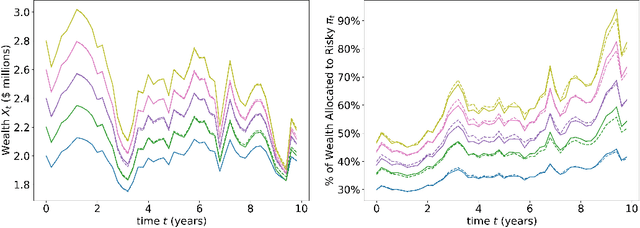
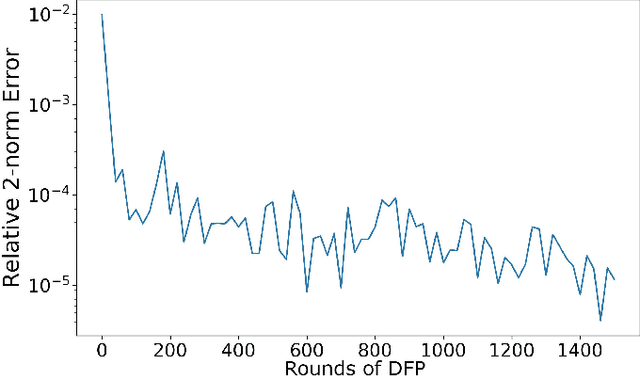
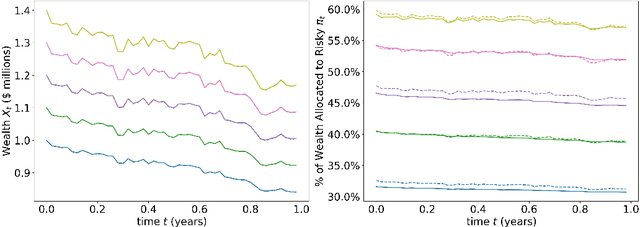
Abstract:In this paper, we propose a numerical methodology for finding the closed-loop Nash equilibrium of stochastic delay differential games through deep learning. These games are prevalent in finance and economics where multi-agent interaction and delayed effects are often desired features in a model, but are introduced at the expense of increased dimensionality of the problem. This increased dimensionality is especially significant as that arising from the number of players is coupled with the potential infinite dimensionality caused by the delay. Our approach involves parameterizing the controls of each player using distinct recurrent neural networks. These recurrent neural network-based controls are then trained using a modified version of Brown's fictitious play, incorporating deep learning techniques. To evaluate the effectiveness of our methodology, we test it on finance-related problems with known solutions. Furthermore, we also develop new problems and derive their analytical Nash equilibrium solutions, which serve as additional benchmarks for assessing the performance of our proposed deep learning approach.
Machine Learning and Polymer Self-Consistent Field Theory in Two Spatial Dimensions
Dec 16, 2022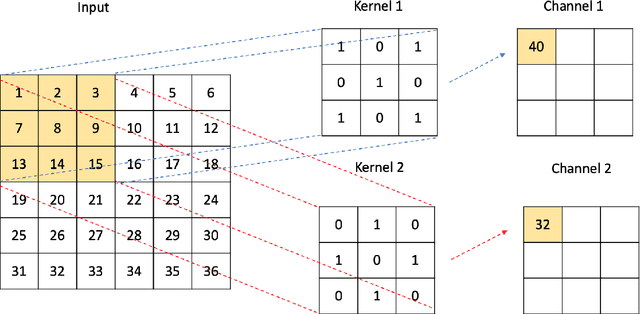
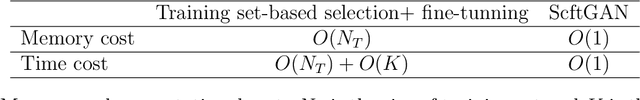
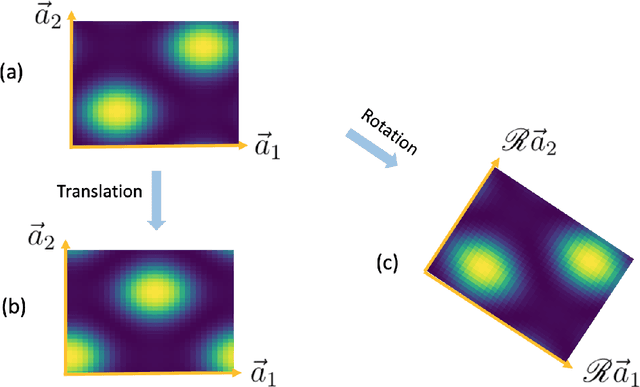

Abstract:A computational framework that leverages data from self-consistent field theory simulations with deep learning to accelerate the exploration of parameter space for block copolymers is presented. This is a substantial two-dimensional extension of the framework introduced in [1]. Several innovations and improvements are proposed. (1) A Sobolev space-trained, convolutional neural network (CNN) is employed to handle the exponential dimension increase of the discretized, local average monomer density fields and to strongly enforce both spatial translation and rotation invariance of the predicted, field-theoretic intensive Hamiltonian. (2) A generative adversarial network (GAN) is introduced to efficiently and accurately predict saddle point, local average monomer density fields without resorting to gradient descent methods that employ the training set. This GAN approach yields important savings of both memory and computational cost. (3) The proposed machine learning framework is successfully applied to 2D cell size optimization as a clear illustration of its broad potential to accelerate the exploration of parameter space for discovering polymer nanostructures. Extensions to three-dimensional phase discovery appear to be feasible.
Pandemic Control, Game Theory and Machine Learning
Aug 18, 2022
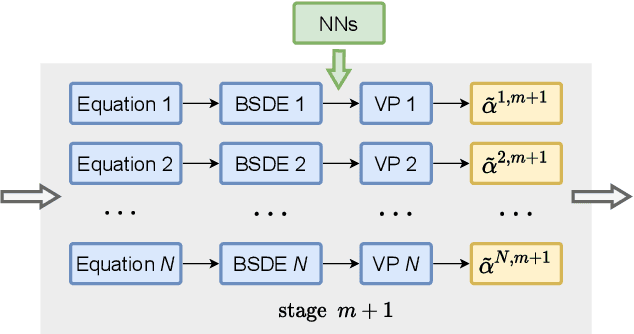
Abstract:Game theory has been an effective tool in the control of disease spread and in suggesting optimal policies at both individual and area levels. In this AMS Notices article, we focus on the decision-making development for the intervention of COVID-19, aiming to provide mathematical models and efficient machine learning methods, and justifications for related policies that have been implemented in the past and explain how the authorities' decisions affect their neighboring regions from a game theory viewpoint.
Optimal Policies for a Pandemic: A Stochastic Game Approach and a Deep Learning Algorithm
Dec 12, 2020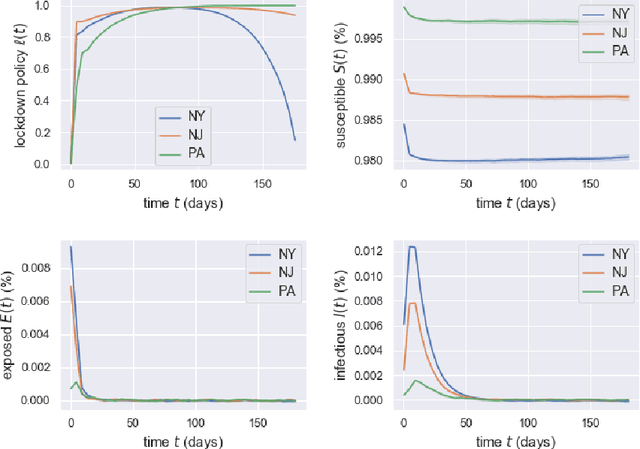
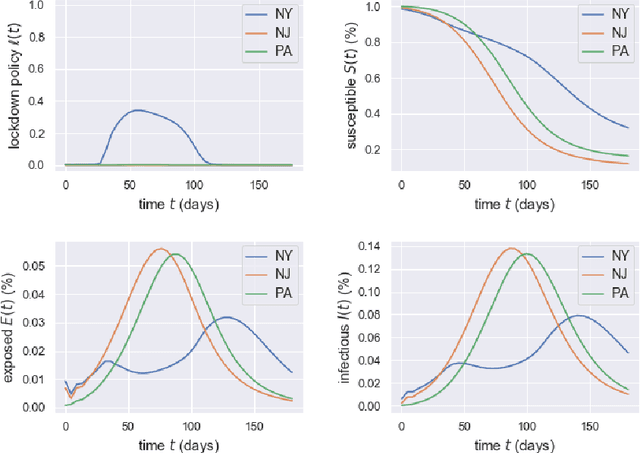
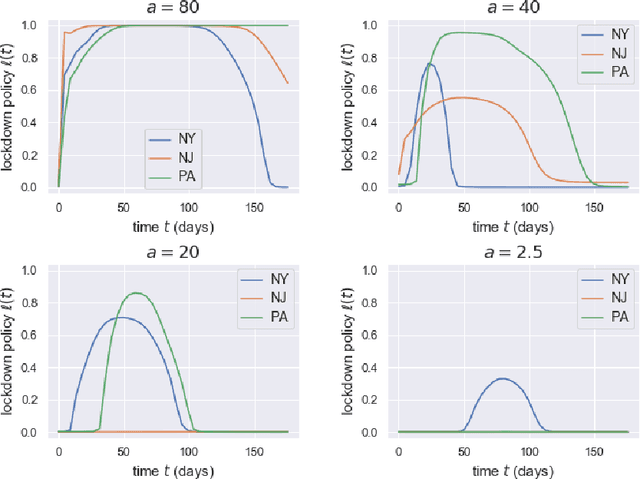
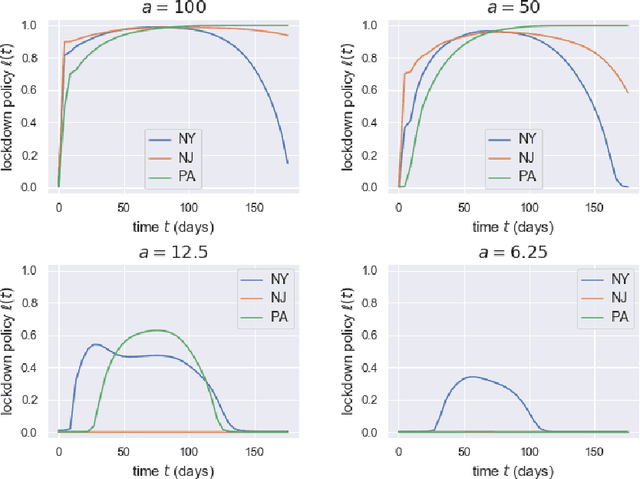
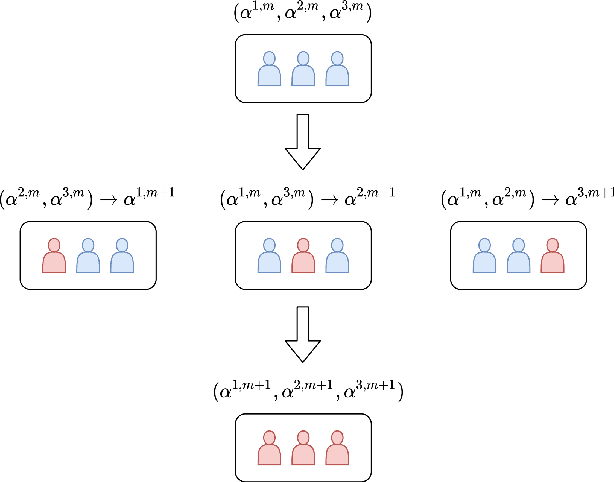
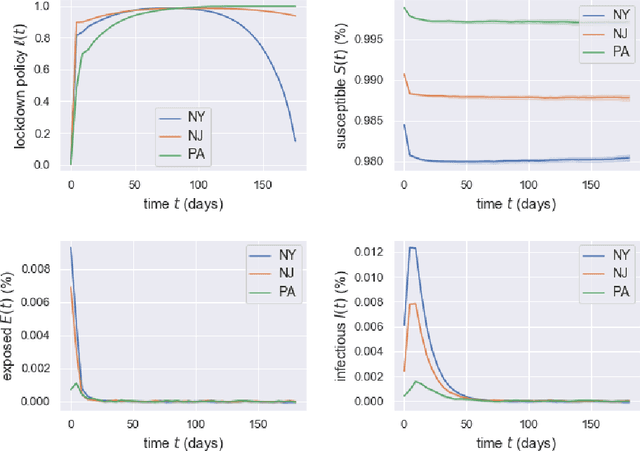
Abstract:Game theory has been an effective tool in the control of disease spread and in suggesting optimal policies at both individual and area levels. In this paper, we propose a multi-region SEIR model based on stochastic differential game theory, aiming to formulate optimal regional policies for infectious diseases. Specifically, we enhance the standard epidemic SEIR model by taking into account the social and health policies issued by multiple region planners. This enhancement makes the model more realistic and powerful. However, it also introduces a formidable computational challenge due to the high dimensionality of the solution space brought by the presence of multiple regions. This significant numerical difficulty of the model structure motivates us to generalize the deep fictitious algorithm introduced in [Han and Hu, MSML2020, pp.221--245, PMLR, 2020] and develop an improved algorithm to overcome the curse of dimensionality. We apply the proposed model and algorithm to study the COVID-19 pandemic in three states: New York, New Jersey, and Pennsylvania. The model parameters are estimated from real data posted by the Centers for Disease Control and Prevention (CDC). We are able to show the effects of the lockdown/travel ban policy on the spread of COVID-19 for each state and how their policies affect each other.
Kernel Treelets
Dec 12, 2018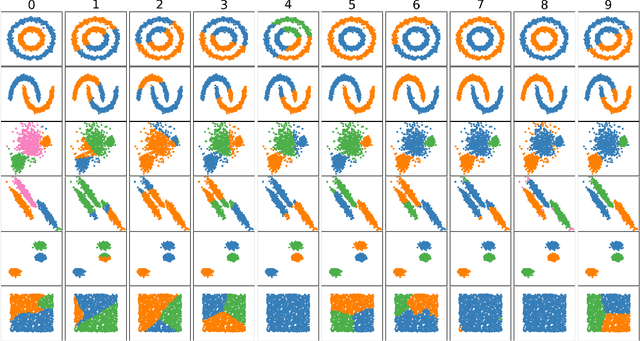
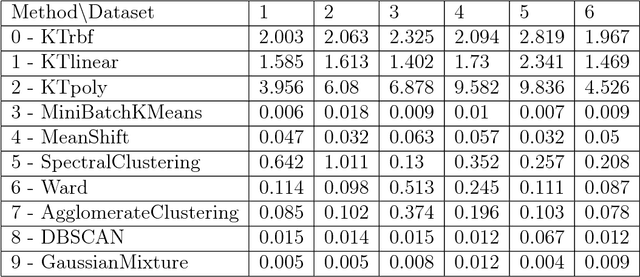
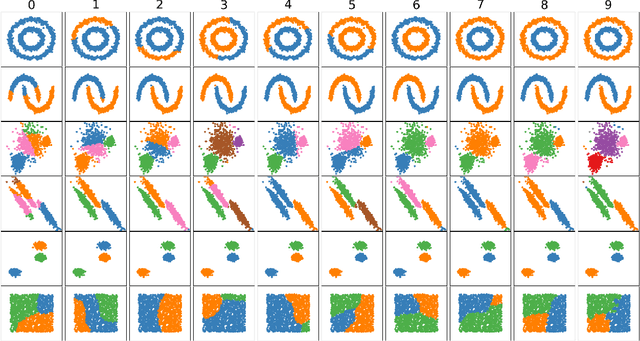
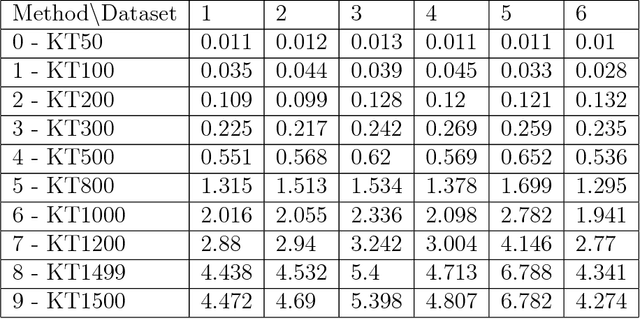
Abstract:A new method for hierarchical clustering is presented. It combines treelets, a particular multiscale decomposition of data, with a projection on a reproducing kernel Hilbert space. The proposed approach, called kernel treelets (KT), effectively substitutes the correlation coefficient matrix used in treelets with a symmetric, positive semi-definite matrix efficiently constructed from a kernel function. Unlike most clustering methods, which require data sets to be numeric, KT can be applied to more general data and yield a multi-resolution sequence of basis on the data directly in feature space. The effectiveness and potential of KT in clustering analysis is illustrated with some examples.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge