Sphere2Vec: A General-Purpose Location Representation Learning over a Spherical Surface for Large-Scale Geospatial Predictions

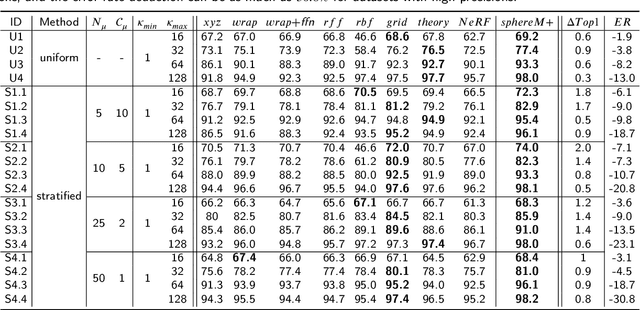
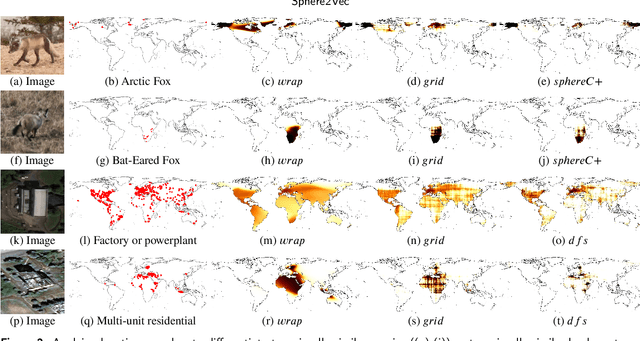
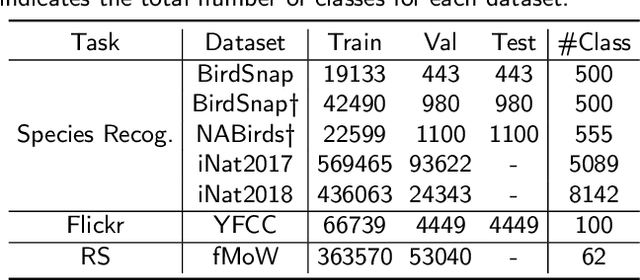
Generating learning-friendly representations for points in space is a fundamental and long-standing problem in ML. Recently, multi-scale encoding schemes (such as Space2Vec and NeRF) were proposed to directly encode any point in 2D/3D Euclidean space as a high-dimensional vector, and has been successfully applied to various geospatial prediction and generative tasks. However, all current 2D and 3D location encoders are designed to model point distances in Euclidean space. So when applied to large-scale real-world GPS coordinate datasets, which require distance metric learning on the spherical surface, both types of models can fail due to the map projection distortion problem (2D) and the spherical-to-Euclidean distance approximation error (3D). To solve these problems, we propose a multi-scale location encoder called Sphere2Vec which can preserve spherical distances when encoding point coordinates on a spherical surface. We developed a unified view of distance-reserving encoding on spheres based on the DFS. We also provide theoretical proof that the Sphere2Vec preserves the spherical surface distance between any two points, while existing encoding schemes do not. Experiments on 20 synthetic datasets show that Sphere2Vec can outperform all baseline models on all these datasets with up to 30.8% error rate reduction. We then apply Sphere2Vec to three geo-aware image classification tasks - fine-grained species recognition, Flickr image recognition, and remote sensing image classification. Results on 7 real-world datasets show the superiority of Sphere2Vec over multiple location encoders on all three tasks. Further analysis shows that Sphere2Vec outperforms other location encoder models, especially in the polar regions and data-sparse areas because of its nature for spherical surface distance preservation. Code and data are available at https://gengchenmai.github.io/sphere2vec-website/.

Machine Learning and Polymer Self-Consistent Field Theory in Two Spatial Dimensions

A computational framework that leverages data from self-consistent field theory simulations with deep learning to accelerate the exploration of parameter space for block copolymers is presented. This is a substantial two-dimensional extension of the framework introduced in [1]. Several innovations and improvements are proposed. (1) A Sobolev space-trained, convolutional neural network (CNN) is employed to handle the exponential dimension increase of the discretized, local average monomer density fields and to strongly enforce both spatial translation and rotation invariance of the predicted, field-theoretic intensive Hamiltonian. (2) A generative adversarial network (GAN) is introduced to efficiently and accurately predict saddle point, local average monomer density fields without resorting to gradient descent methods that employ the training set. This GAN approach yields important savings of both memory and computational cost. (3) The proposed machine learning framework is successfully applied to 2D cell size optimization as a clear illustration of its broad potential to accelerate the exploration of parameter space for discovering polymer nanostructures. Extensions to three-dimensional phase discovery appear to be feasible.

Towards General-Purpose Representation Learning of Polygonal Geometries

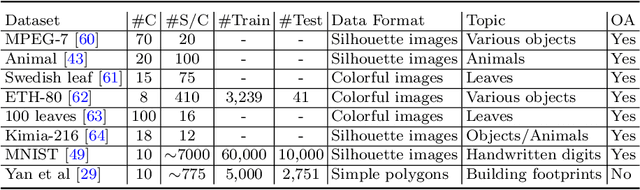
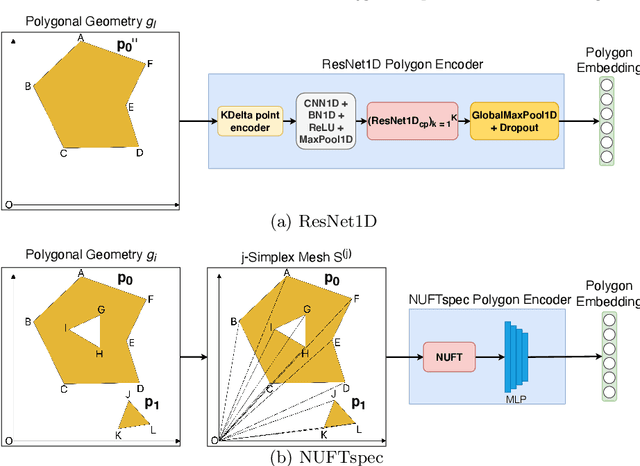
Neural network representation learning for spatial data is a common need for geographic artificial intelligence (GeoAI) problems. In recent years, many advancements have been made in representation learning for points, polylines, and networks, whereas little progress has been made for polygons, especially complex polygonal geometries. In this work, we focus on developing a general-purpose polygon encoding model, which can encode a polygonal geometry (with or without holes, single or multipolygons) into an embedding space. The result embeddings can be leveraged directly (or finetuned) for downstream tasks such as shape classification, spatial relation prediction, and so on. To achieve model generalizability guarantees, we identify a few desirable properties: loop origin invariance, trivial vertex invariance, part permutation invariance, and topology awareness. We explore two different designs for the encoder: one derives all representations in the spatial domain; the other leverages spectral domain representations. For the spatial domain approach, we propose ResNet1D, a 1D CNN-based polygon encoder, which uses circular padding to achieve loop origin invariance on simple polygons. For the spectral domain approach, we develop NUFTspec based on Non-Uniform Fourier Transformation (NUFT), which naturally satisfies all the desired properties. We conduct experiments on two tasks: 1) shape classification based on MNIST; 2) spatial relation prediction based on two new datasets - DBSR-46K and DBSR-cplx46K. Our results show that NUFTspec and ResNet1D outperform multiple existing baselines with significant margins. While ResNet1D suffers from model performance degradation after shape-invariance geometry modifications, NUFTspec is very robust to these modifications due to the nature of the NUFT.

Pandemic Control, Game Theory and Machine Learning

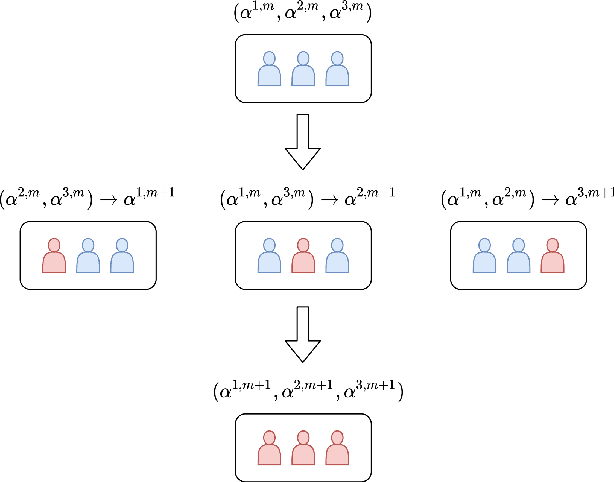
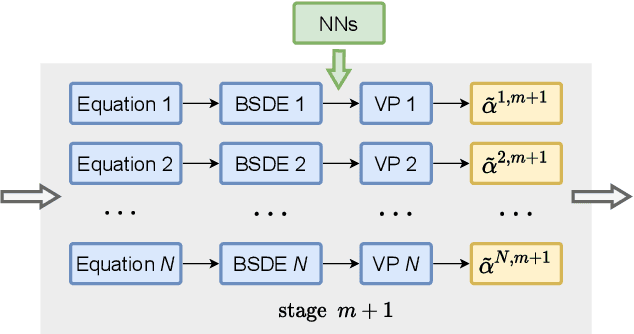
Game theory has been an effective tool in the control of disease spread and in suggesting optimal policies at both individual and area levels. In this AMS Notices article, we focus on the decision-making development for the intervention of COVID-19, aiming to provide mathematical models and efficient machine learning methods, and justifications for related policies that have been implemented in the past and explain how the authorities' decisions affect their neighboring regions from a game theory viewpoint.

Sphere2Vec: Multi-Scale Representation Learning over a Spherical Surface for Geospatial Predictions

Generating learning-friendly representations for points in a 2D space is a fundamental and long-standing problem in machine learning. Recently, multi-scale encoding schemes (such as Space2Vec) were proposed to directly encode any point in 2D space as a high-dimensional vector, and has been successfully applied to various (geo)spatial prediction tasks. However, a map projection distortion problem rises when applying location encoding models to large-scale real-world GPS coordinate datasets (e.g., species images taken all over the world) - all current location encoding models are designed for encoding points in a 2D (Euclidean) space but not on a spherical surface, e.g., earth surface. To solve this problem, we propose a multi-scale location encoding model called Sphere2V ec which directly encodes point coordinates on a spherical surface while avoiding the mapprojection distortion problem. We provide theoretical proof that the Sphere2Vec encoding preserves the spherical surface distance between any two points. We also developed a unified view of distance-reserving encoding on spheres based on the Double Fourier Sphere (DFS). We apply Sphere2V ec to the geo-aware image classification task. Our analysis shows that Sphere2V ec outperforms other 2D space location encoder models especially on the polar regions and data-sparse areas for image classification tasks because of its nature for spherical surface distance preservation.

Optimal Policies for a Pandemic: A Stochastic Game Approach and a Deep Learning Algorithm

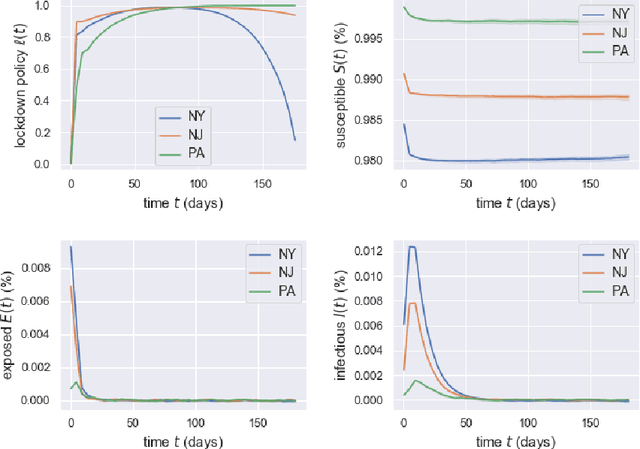
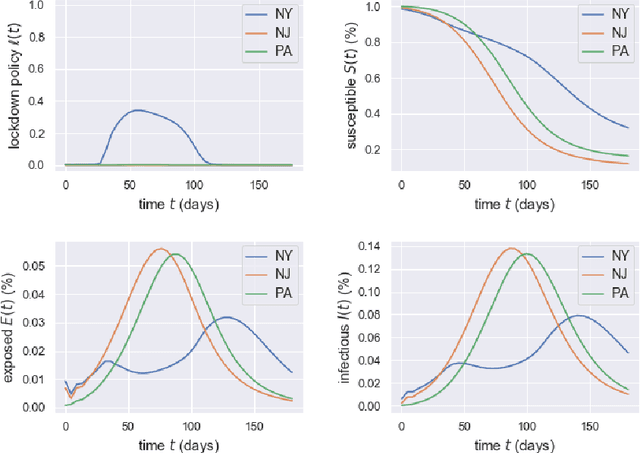
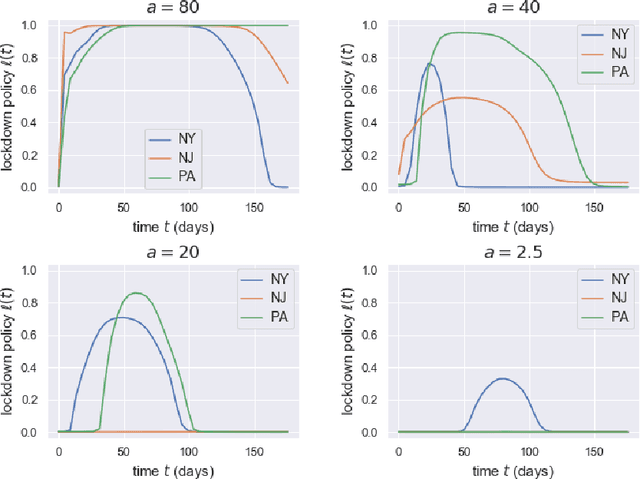
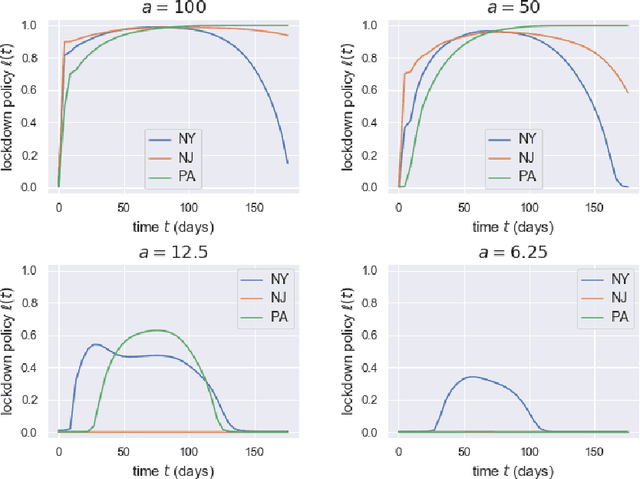
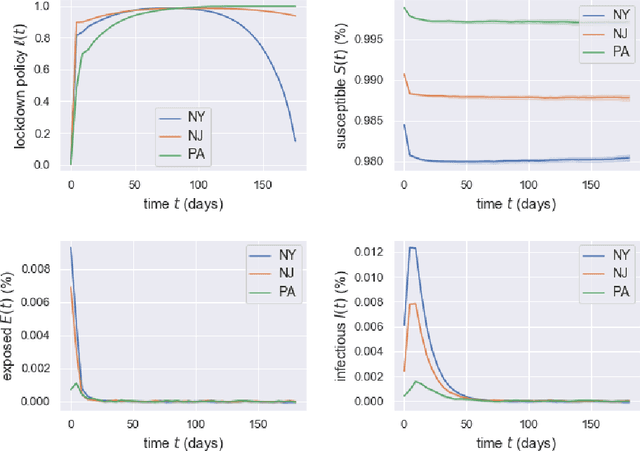
Game theory has been an effective tool in the control of disease spread and in suggesting optimal policies at both individual and area levels. In this paper, we propose a multi-region SEIR model based on stochastic differential game theory, aiming to formulate optimal regional policies for infectious diseases. Specifically, we enhance the standard epidemic SEIR model by taking into account the social and health policies issued by multiple region planners. This enhancement makes the model more realistic and powerful. However, it also introduces a formidable computational challenge due to the high dimensionality of the solution space brought by the presence of multiple regions. This significant numerical difficulty of the model structure motivates us to generalize the deep fictitious algorithm introduced in [Han and Hu, MSML2020, pp.221--245, PMLR, 2020] and develop an improved algorithm to overcome the curse of dimensionality. We apply the proposed model and algorithm to study the COVID-19 pandemic in three states: New York, New Jersey, and Pennsylvania. The model parameters are estimated from real data posted by the Centers for Disease Control and Prevention (CDC). We are able to show the effects of the lockdown/travel ban policy on the spread of COVID-19 for each state and how their policies affect each other.

Enhancing the Locality and Breaking the Memory Bottleneck of Transformer on Time Series Forecasting

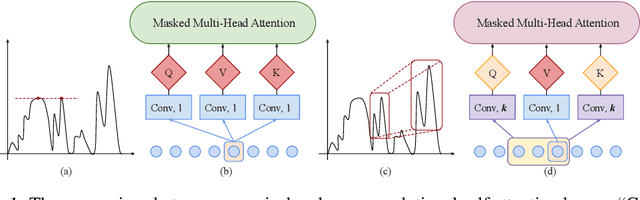
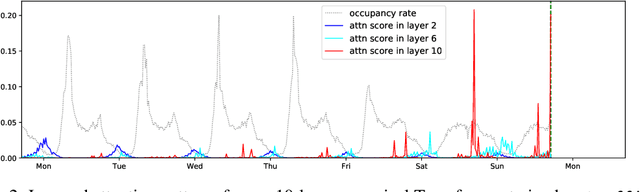
Time series forecasting is an important problem across many domains, including predictions of solar plant energy output, electricity consumption, and traffic jam situation. In this paper, we propose to tackle such forecasting problem with Transformer. Although impressed by its performance in our preliminary study, we found its two major weaknesses: (1) locality-agnostics: the point-wise dot-product self attention in canonical Transformer architecture is insensitive to local context, which can make the model prone to anomalies in time series; (2) memory bottleneck: space complexity of canonical Transformer grows quadratically with sequence length $L$, making modeling long time series infeasible. In order to solve these two issues, we first propose convolutional self attention by producing queries and keys with causal convolution so that local context can be better incorporated into attention mechanism. Then, we propose LogSparse Transformer with only $O(L(\log L)^{2})$ memory cost, improving the time series forecasting in finer granularity under constrained memory budget. Our experiments on both synthetic data and real-world datasets show that it compares favorably to the state-of-the-art.