Towards General-Purpose Representation Learning of Polygonal Geometries

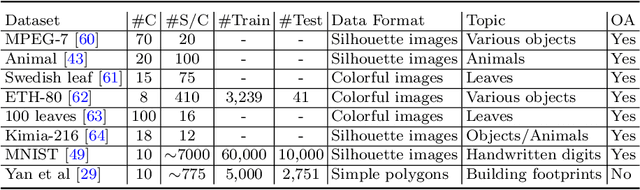
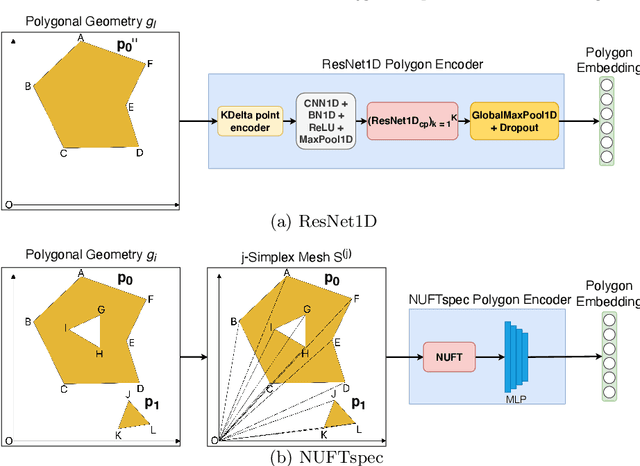
Neural network representation learning for spatial data is a common need for geographic artificial intelligence (GeoAI) problems. In recent years, many advancements have been made in representation learning for points, polylines, and networks, whereas little progress has been made for polygons, especially complex polygonal geometries. In this work, we focus on developing a general-purpose polygon encoding model, which can encode a polygonal geometry (with or without holes, single or multipolygons) into an embedding space. The result embeddings can be leveraged directly (or finetuned) for downstream tasks such as shape classification, spatial relation prediction, and so on. To achieve model generalizability guarantees, we identify a few desirable properties: loop origin invariance, trivial vertex invariance, part permutation invariance, and topology awareness. We explore two different designs for the encoder: one derives all representations in the spatial domain; the other leverages spectral domain representations. For the spatial domain approach, we propose ResNet1D, a 1D CNN-based polygon encoder, which uses circular padding to achieve loop origin invariance on simple polygons. For the spectral domain approach, we develop NUFTspec based on Non-Uniform Fourier Transformation (NUFT), which naturally satisfies all the desired properties. We conduct experiments on two tasks: 1) shape classification based on MNIST; 2) spatial relation prediction based on two new datasets - DBSR-46K and DBSR-cplx46K. Our results show that NUFTspec and ResNet1D outperform multiple existing baselines with significant margins. While ResNet1D suffers from model performance degradation after shape-invariance geometry modifications, NUFTspec is very robust to these modifications due to the nature of the NUFT.

Leveraging Bayesian Analysis To Improve Accuracy of Approximate Models

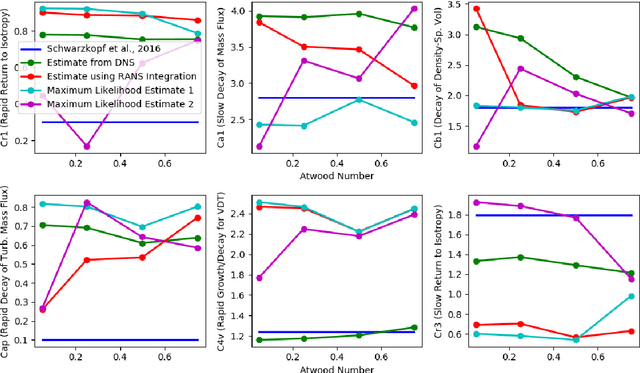
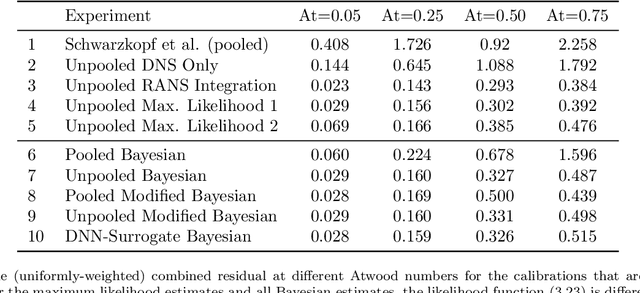
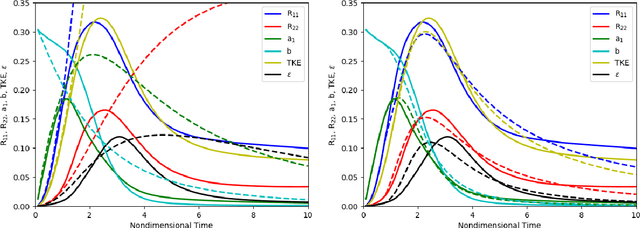
We focus on improving the accuracy of an approximate model of a multiscale dynamical system that uses a set of parameter-dependent terms to account for the effects of unresolved or neglected dynamics on resolved scales. We start by considering various methods of calibrating and analyzing such a model given a few well-resolved simulations. After presenting results for various point estimates and discussing some of their shortcomings, we demonstrate (a) the potential of hierarchical Bayesian analysis to uncover previously unanticipated physical dependencies in the approximate model, and (b) how such insights can then be used to improve the model. In effect parametric dependencies found from the Bayesian analysis are used to improve structural aspects of the model. While we choose to illustrate the procedure in the context of a closure model for buoyancy-driven, variable-density turbulence, the statistical nature of the approach makes it more generally applicable. Towards addressing issues of increased computational cost associated with the procedure, we demonstrate the use of a neural network based surrogate in accelerating the posterior sampling process and point to recent developments in variational inference as an alternative methodology for greatly mitigating such costs. We conclude by suggesting that modern validation and uncertainty quantification techniques such as the ones we consider have a valuable role to play in the development and improvement of approximate models.