Kernel Treelets
Paper and Code
Dec 12, 2018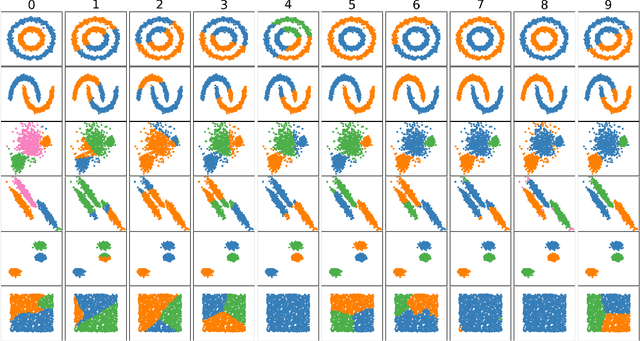
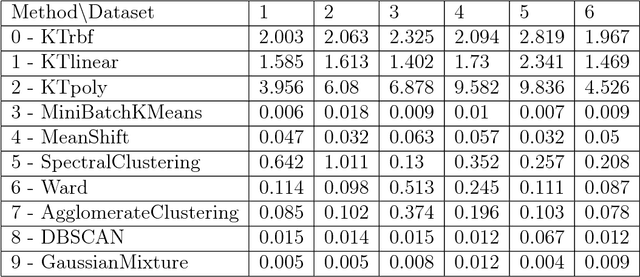
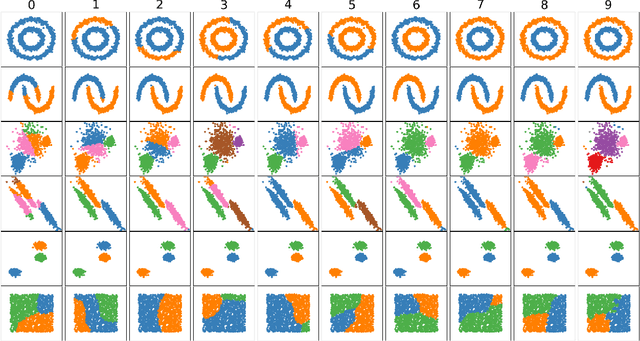
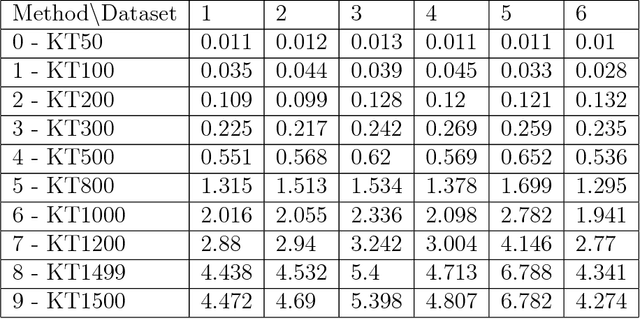
A new method for hierarchical clustering is presented. It combines treelets, a particular multiscale decomposition of data, with a projection on a reproducing kernel Hilbert space. The proposed approach, called kernel treelets (KT), effectively substitutes the correlation coefficient matrix used in treelets with a symmetric, positive semi-definite matrix efficiently constructed from a kernel function. Unlike most clustering methods, which require data sets to be numeric, KT can be applied to more general data and yield a multi-resolution sequence of basis on the data directly in feature space. The effectiveness and potential of KT in clustering analysis is illustrated with some examples.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge