Learning High-Dimensional McKean-Vlasov Forward-Backward Stochastic Differential Equations with General Distribution Dependence

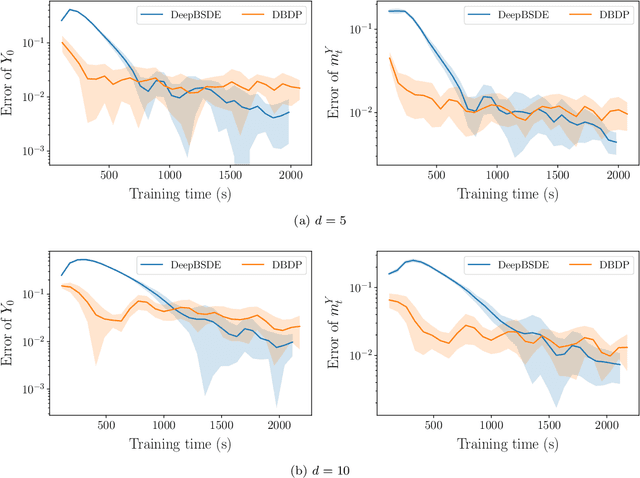
One of the core problems in mean-field control and mean-field games is to solve the corresponding McKean-Vlasov forward-backward stochastic differential equations (MV-FBSDEs). Most existing methods are tailored to special cases in which the mean-field interaction only depends on expectation or other moments and thus inadequate to solve problems when the mean-field interaction has full distribution dependence. In this paper, we propose a novel deep learning method for computing MV-FBSDEs with a general form of mean-field interactions. Specifically, built on fictitious play, we recast the problem into repeatedly solving standard FBSDEs with explicit coefficient functions. These coefficient functions are used to approximate the MV-FBSDEs' model coefficients with full distribution dependence, and are updated by solving another supervising learning problem using training data simulated from the last iteration's FBSDE solutions. We use deep neural networks to solve standard BSDEs and approximate coefficient functions in order to solve high-dimensional MV-FBSDEs. Under proper assumptions on the learned functions, we prove that the convergence of the proposed method is free of the curse of dimensionality (CoD) by using the generalized maximum mean discrepancy metric previously developed in [Han, Hu and Long, arXiv:2104.12036]. The proved theorem shows the advantage of the method in high dimensions. We present the numerical performance in high-dimensional MV-FBSDE problems, including a mean-field game example of the well-known Cucker-Smale model whose cost depends on the full distribution of the forward process.