Wanning Chen
Match Made with Matrix Completion: Efficient Learning under Matching Interference
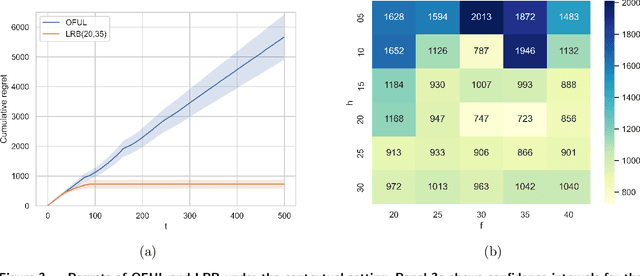
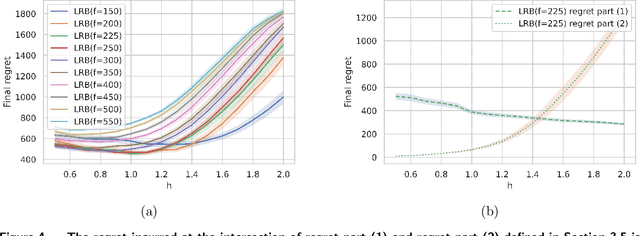
Jan 11, 2026Abstract:Matching markets face increasing needs to learn the matching qualities between demand and supply for effective design of matching policies. In practice, the matching rewards are high-dimensional due to the growing diversity of participants. We leverage a natural low-rank matrix structure of the matching rewards in these two-sided markets, and propose to utilize matrix completion to accelerate reward learning with limited offline data. A unique property for matrix completion in this setting is that the entries of the reward matrix are observed with matching interference -- i.e., the entries are not observed independently but dependently due to matching or budget constraints. Such matching dependence renders unique technical challenges, such as sub-optimality or inapplicability of the existing analytical tools in the matrix completion literature, since they typically rely on sample independence. In this paper, we first show that standard nuclear norm regularization remains theoretically effective under matching interference. We provide a near-optimal Frobenius norm guarantee in this setting, coupled with a new analytical technique. Next, to guide certain matching decisions, we develop a novel ``double-enhanced'' estimator, based off the nuclear norm estimator, with a near-optimal entry-wise guarantee. Our double-enhancement procedure can apply to broader sampling schemes even with dependence, which may be of independent interest. Additionally, we extend our approach to online learning settings with matching constraints such as optimal matching and stable matching, and present improved regret bounds in matrix dimensions. Finally, we demonstrate the practical value of our methods using both synthetic data and real data of labor markets.
Speed Up the Cold-Start Learning in Two-Sided Bandits with Many Arms
Oct 01, 2022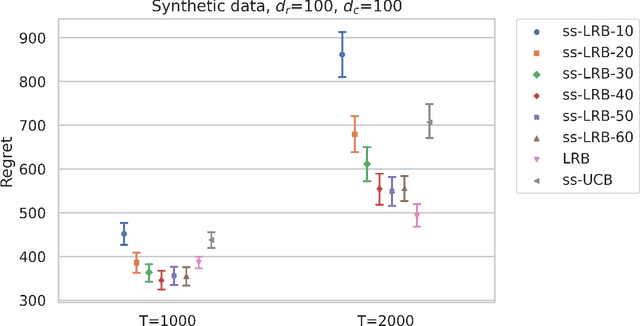
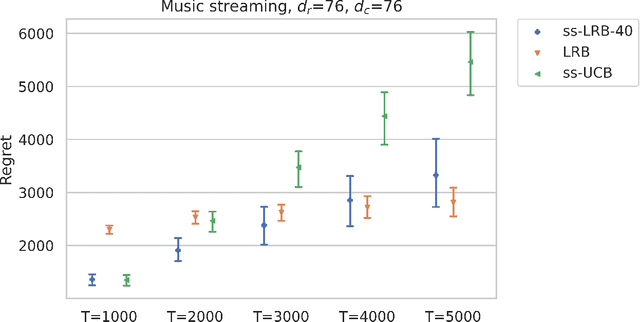
Abstract:Multi-armed bandit (MAB) algorithms are efficient approaches to reduce the opportunity cost of online experimentation and are used by companies to find the best product from periodically refreshed product catalogs. However, these algorithms face the so-called cold-start at the onset of the experiment due to a lack of knowledge of customer preferences for new products, requiring an initial data collection phase known as the burning period. During this period, MAB algorithms operate like randomized experiments, incurring large burning costs which scale with the large number of products. We attempt to reduce the burning by identifying that many products can be cast into two-sided products, and then naturally model the rewards of the products with a matrix, whose rows and columns represent the two sides respectively. Next, we design two-phase bandit algorithms that first use subsampling and low-rank matrix estimation to obtain a substantially smaller targeted set of products and then apply a UCB procedure on the target products to find the best one. We theoretically show that the proposed algorithms lower costs and expedite the experiment in cases when there is limited experimentation time along with a large product set. Our analysis also reveals three regimes of long, short, and ultra-short horizon experiments, depending on dimensions of the matrix. Empirical evidence from both synthetic data and a real-world dataset on music streaming services validates this superior performance.
Learning to Recommend Using Non-Uniform Data
Oct 21, 2021
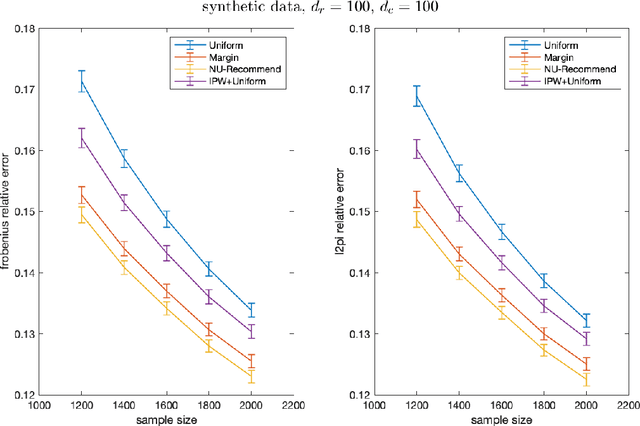


Abstract:Learning user preferences for products based on their past purchases or reviews is at the cornerstone of modern recommendation engines. One complication in this learning task is that some users are more likely to purchase products or review them, and some products are more likely to be purchased or reviewed by the users. This non-uniform pattern degrades the power of many existing recommendation algorithms, as they assume that the observed data is sampled uniformly at random among user-product pairs. In addition, existing literature on modeling non-uniformity either assume user interests are independent of the products, or lack theoretical understanding. In this paper, we first model the user-product preferences as a partially observed matrix with non-uniform observation pattern. Next, building on the literature about low-rank matrix estimation, we introduce a new weighted trace-norm penalized regression to predict unobserved values of the matrix. We then prove an upper bound for the prediction error of our proposed approach. Our upper bound is a function of a number of parameters that are based on a certain weight matrix that depends on the joint distribution of users and products. Utilizing this observation, we introduce a new optimization problem to select a weight matrix that minimizes the upper bound on the prediction error. The final product is a new estimator, NU-Recommend, that outperforms existing methods in both synthetic and real datasets.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge