Learning to Recommend Using Non-Uniform Data
Paper and Code
Oct 21, 2021
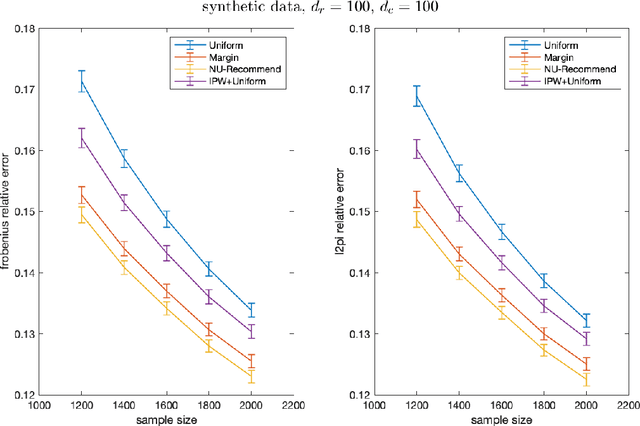


Learning user preferences for products based on their past purchases or reviews is at the cornerstone of modern recommendation engines. One complication in this learning task is that some users are more likely to purchase products or review them, and some products are more likely to be purchased or reviewed by the users. This non-uniform pattern degrades the power of many existing recommendation algorithms, as they assume that the observed data is sampled uniformly at random among user-product pairs. In addition, existing literature on modeling non-uniformity either assume user interests are independent of the products, or lack theoretical understanding. In this paper, we first model the user-product preferences as a partially observed matrix with non-uniform observation pattern. Next, building on the literature about low-rank matrix estimation, we introduce a new weighted trace-norm penalized regression to predict unobserved values of the matrix. We then prove an upper bound for the prediction error of our proposed approach. Our upper bound is a function of a number of parameters that are based on a certain weight matrix that depends on the joint distribution of users and products. Utilizing this observation, we introduce a new optimization problem to select a weight matrix that minimizes the upper bound on the prediction error. The final product is a new estimator, NU-Recommend, that outperforms existing methods in both synthetic and real datasets.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge