Higher-Order Causal Message Passing for Experimentation with Complex Interference
Paper and Code
Nov 01, 2024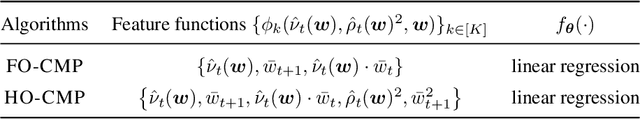
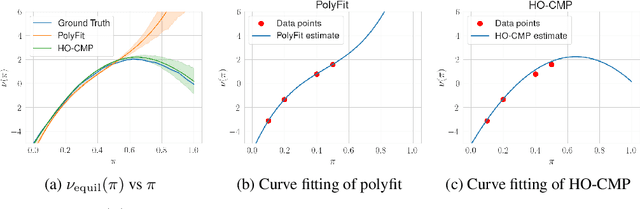
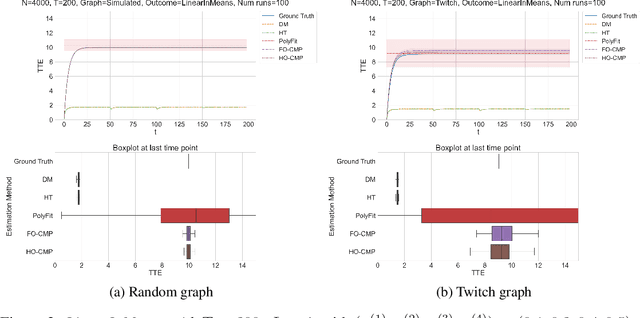
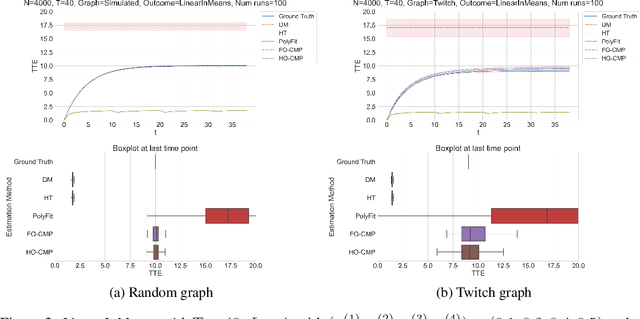
Accurate estimation of treatment effects is essential for decision-making across various scientific fields. This task, however, becomes challenging in areas like social sciences and online marketplaces, where treating one experimental unit can influence outcomes for others through direct or indirect interactions. Such interference can lead to biased treatment effect estimates, particularly when the structure of these interactions is unknown. We address this challenge by introducing a new class of estimators based on causal message-passing, specifically designed for settings with pervasive, unknown interference. Our estimator draws on information from the sample mean and variance of unit outcomes and treatments over time, enabling efficient use of observed data to estimate the evolution of the system state. Concretely, we construct non-linear features from the moments of unit outcomes and treatments and then learn a function that maps these features to future mean and variance of unit outcomes. This allows for the estimation of the treatment effect over time. Extensive simulations across multiple domains, using synthetic and real network data, demonstrate the efficacy of our approach in estimating total treatment effect dynamics, even in cases where interference exhibits non-monotonic behavior in the probability of treatment.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge