On Aligning Prediction Models with Clinical Experiential Learning: A Prostate Cancer Case Study

Over the past decade, the use of machine learning (ML) models in healthcare applications has rapidly increased. Despite high performance, modern ML models do not always capture patterns the end user requires. For example, a model may predict a non-monotonically decreasing relationship between cancer stage and survival, keeping all other features fixed. In this paper, we present a reproducible framework for investigating this misalignment between model behavior and clinical experiential learning, focusing on the effects of underspecification of modern ML pipelines. In a prostate cancer outcome prediction case study, we first identify and address these inconsistencies by incorporating clinical knowledge, collected by a survey, via constraints into the ML model, and subsequently analyze the impact on model performance and behavior across degrees of underspecification. The approach shows that aligning the ML model with clinical experiential learning is possible without compromising performance. Motivated by recent literature in generative AI, we further examine the feasibility of a feedback-driven alignment approach in non-generative AI clinical risk prediction models through a randomized experiment with clinicians. Our findings illustrate that, by eliciting clinicians' model preferences using our proposed methodology, the larger the difference in how the constrained and unconstrained models make predictions for a patient, the more apparent the difference is in clinical interpretation.

Can We Validate Counterfactual Estimations in the Presence of General Network Interference?

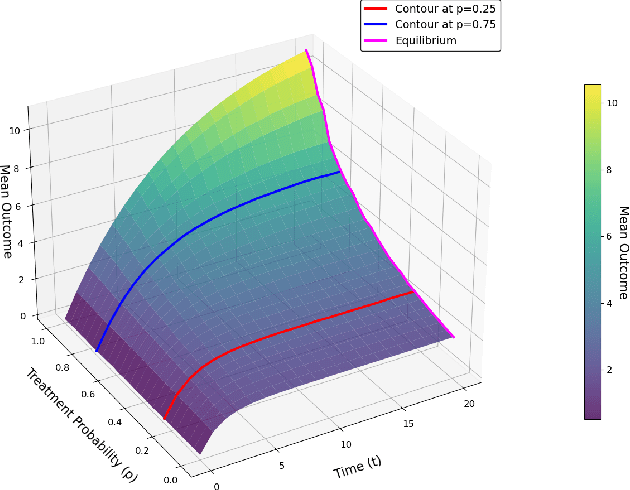
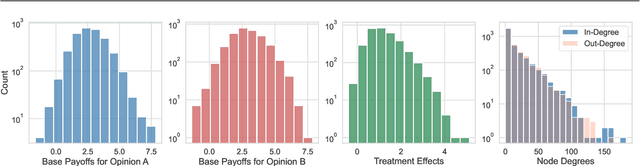
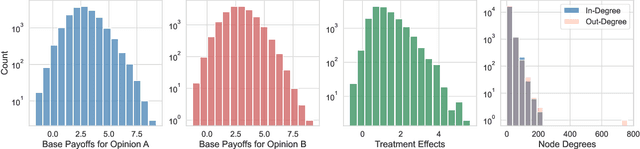
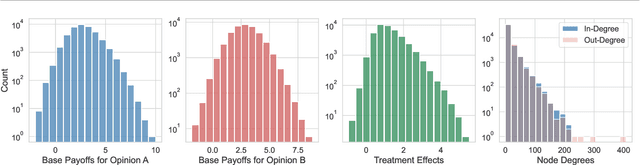
In experimental settings with network interference, a unit's treatment can influence outcomes of other units, challenging both causal effect estimation and its validation. Classic validation approaches fail as outcomes are only observable under one treatment scenario and exhibit complex correlation patterns due to interference. To address these challenges, we introduce a new framework enabling cross-validation for counterfactual estimation. At its core is our distribution-preserving network bootstrap method -- a theoretically-grounded approach inspired by approximate message passing. This method creates multiple subpopulations while preserving the underlying distribution of network effects. We extend recent causal message-passing developments by incorporating heterogeneous unit-level characteristics and varying local interactions, ensuring reliable finite-sample performance through non-asymptotic analysis. We also develop and publicly release a comprehensive benchmark toolbox with diverse experimental environments, from networks of interacting AI agents to opinion formation in real-world communities and ride-sharing applications. These environments provide known ground truth values while maintaining realistic complexities, enabling systematic examination of causal inference methods. Extensive evaluation across these environments demonstrates our method's robustness to diverse forms of network interference. Our work provides researchers with both a practical estimation framework and a standardized platform for testing future methodological developments.

Higher-Order Causal Message Passing for Experimentation with Complex Interference

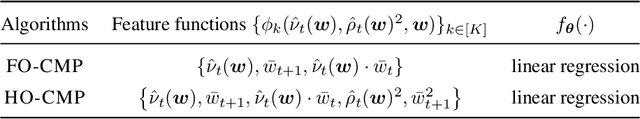
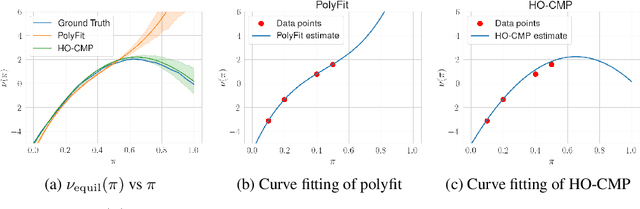
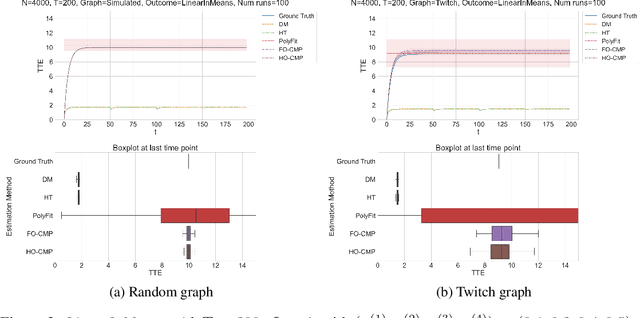
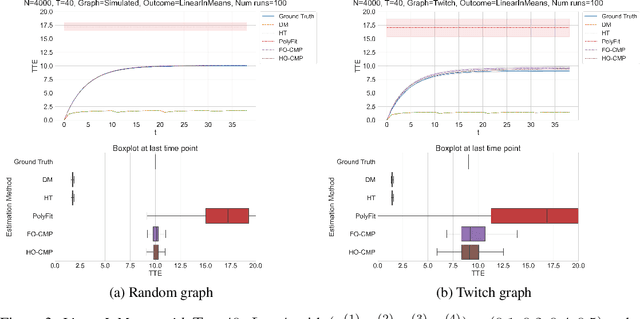
Accurate estimation of treatment effects is essential for decision-making across various scientific fields. This task, however, becomes challenging in areas like social sciences and online marketplaces, where treating one experimental unit can influence outcomes for others through direct or indirect interactions. Such interference can lead to biased treatment effect estimates, particularly when the structure of these interactions is unknown. We address this challenge by introducing a new class of estimators based on causal message-passing, specifically designed for settings with pervasive, unknown interference. Our estimator draws on information from the sample mean and variance of unit outcomes and treatments over time, enabling efficient use of observed data to estimate the evolution of the system state. Concretely, we construct non-linear features from the moments of unit outcomes and treatments and then learn a function that maps these features to future mean and variance of unit outcomes. This allows for the estimation of the treatment effect over time. Extensive simulations across multiple domains, using synthetic and real network data, demonstrate the efficacy of our approach in estimating total treatment effect dynamics, even in cases where interference exhibits non-monotonic behavior in the probability of treatment.

Improved Regret Bound for Safe Reinforcement Learning via Tighter Cost Pessimism and Reward Optimism

This paper studies the safe reinforcement learning problem formulated as an episodic finite-horizon tabular constrained Markov decision process with an unknown transition kernel and stochastic reward and cost functions. We propose a model-based algorithm based on novel cost and reward function estimators that provide tighter cost pessimism and reward optimism. While guaranteeing no constraint violation in every episode, our algorithm achieves a regret upper bound of $\widetilde{\mathcal{O}}((\bar C - \bar C_b)^{-1}H^{2.5} S\sqrt{AK})$ where $\bar C$ is the cost budget for an episode, $\bar C_b$ is the expected cost under a safe baseline policy over an episode, $H$ is the horizon, and $S$, $A$ and $K$ are the number of states, actions, and episodes, respectively. This improves upon the best-known regret upper bound, and when $\bar C- \bar C_b=\Omega(H)$, it nearly matches the regret lower bound of $\Omega(H^{1.5}\sqrt{SAK})$. We deduce our cost and reward function estimators via a Bellman-type law of total variance to obtain tight bounds on the expected sum of the variances of value function estimates. This leads to a tighter dependence on the horizon in the function estimators. We also present numerical results to demonstrate the computational effectiveness of our proposed framework.

Aligning Model Properties via Conformal Risk Control

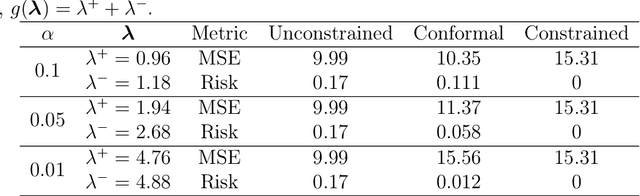
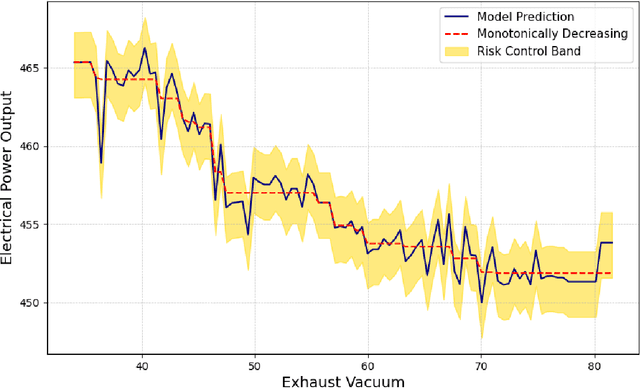
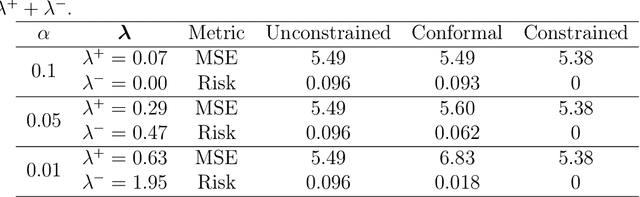
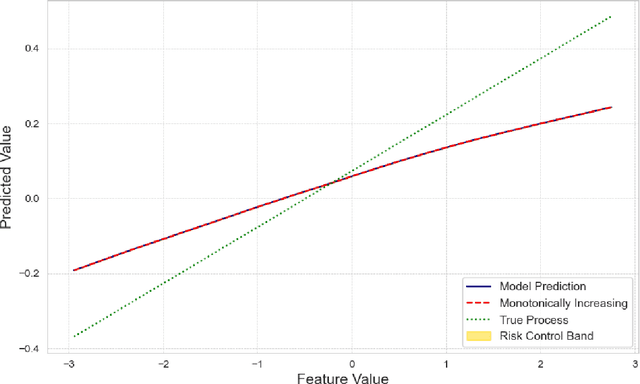
AI model alignment is crucial due to inadvertent biases in training data and the underspecified pipeline in modern machine learning, where numerous models with excellent test set metrics can be produced, yet they may not meet end-user requirements. Recent advances demonstrate that post-training model alignment via human feedback can address some of these challenges. However, these methods are often confined to settings (such as generative AI) where humans can interpret model outputs and provide feedback. In traditional non-generative settings, where model outputs are numerical values or classes, detecting misalignment through single-sample outputs is highly challenging. In this paper we consider an alternative strategy. We propose interpreting model alignment through property testing, defining an aligned model $f$ as one belonging to a subset $\mathcal{P}$ of functions that exhibit specific desired behaviors. We focus on post-processing a pre-trained model $f$ to better align with $\mathcal{P}$ using conformal risk control. Specifically, we develop a general procedure for converting queries for a given property $\mathcal{P}$ to a collection of loss functions suitable for use in a conformal risk control algorithm. We prove a probabilistic guarantee that the resulting conformal interval around $f$ contains a function approximately satisfying $\mathcal{P}$. Given the capabilities of modern AI models with extensive parameters and training data, one might assume alignment issues will resolve naturally. However, increasing training data or parameters in a random feature model doesn't eliminate the need for alignment techniques when pre-training data is biased. We demonstrate our alignment methodology on supervised learning datasets for properties like monotonicity and concavity. Our flexible procedure can be applied to various desired properties.