Improved Regret Bound for Safe Reinforcement Learning via Tighter Cost Pessimism and Reward Optimism

This paper studies the safe reinforcement learning problem formulated as an episodic finite-horizon tabular constrained Markov decision process with an unknown transition kernel and stochastic reward and cost functions. We propose a model-based algorithm based on novel cost and reward function estimators that provide tighter cost pessimism and reward optimism. While guaranteeing no constraint violation in every episode, our algorithm achieves a regret upper bound of $\widetilde{\mathcal{O}}((\bar C - \bar C_b)^{-1}H^{2.5} S\sqrt{AK})$ where $\bar C$ is the cost budget for an episode, $\bar C_b$ is the expected cost under a safe baseline policy over an episode, $H$ is the horizon, and $S$, $A$ and $K$ are the number of states, actions, and episodes, respectively. This improves upon the best-known regret upper bound, and when $\bar C- \bar C_b=\Omega(H)$, it nearly matches the regret lower bound of $\Omega(H^{1.5}\sqrt{SAK})$. We deduce our cost and reward function estimators via a Bellman-type law of total variance to obtain tight bounds on the expected sum of the variances of value function estimates. This leads to a tighter dependence on the horizon in the function estimators. We also present numerical results to demonstrate the computational effectiveness of our proposed framework.

Online Resource Allocation in Episodic Markov Decision Processes

This paper studies a long-term resource allocation problem over multiple periods where each period requires a multi-stage decision-making process. We formulate the problem as an online resource allocation problem in an episodic finite-horizon Markov decision process with unknown non-stationary transitions and stochastic non-stationary reward and resource consumption functions for each episode. We provide an equivalent online linear programming reformulation based on occupancy measures, for which we develop an online mirror descent algorithm. Our online dual mirror descent algorithm for resource allocation deals with uncertainties and errors in estimating the true feasible set, which is of independent interest. We prove that under stochastic reward and resource consumption functions, the expected regret of the online mirror descent algorithm is bounded by $O(\rho^{-1}{H^{3/2}}S\sqrt{AT})$ where $\rho\in(0,1)$ is the budget parameter, $H$ is the length of the horizon, $S$ and $A$ are the numbers of states and actions, and $T$ is the number of episodes.

Projection-Free Online Convex Optimization with Stochastic Constraints

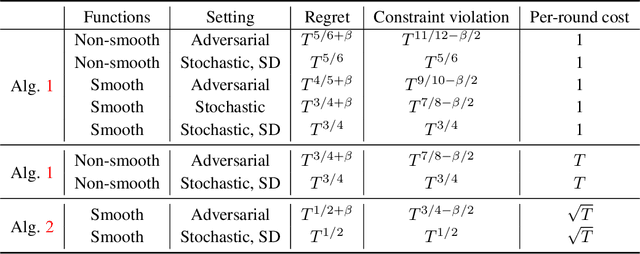
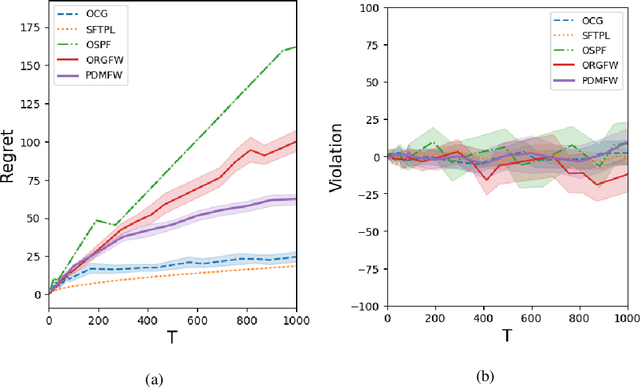
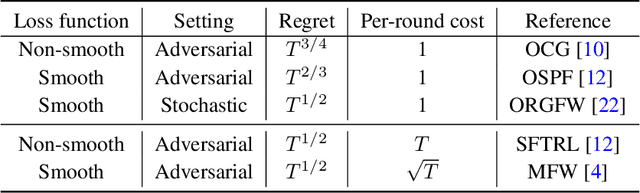
This paper develops projection-free algorithms for online convex optimization with stochastic constraints. We design an online primal-dual projection-free framework that can take any projection-free algorithms developed for online convex optimization with no long-term constraint. With this general template, we deduce sublinear regret and constraint violation bounds for various settings. Moreover, for the case where the loss and constraint functions are smooth, we develop a primal-dual conditional gradient method that achieves $O(\sqrt{T})$ regret and $O(T^{3/4})$ constraint violations. Furthermore, for the setting where the loss and constraint functions are stochastic and strong duality holds for the associated offline stochastic optimization problem, we prove that the constraint violation can be reduced to have the same asymptotic growth as the regret.