Mistake, Manipulation and Margin Guarantees in Online Strategic Classification

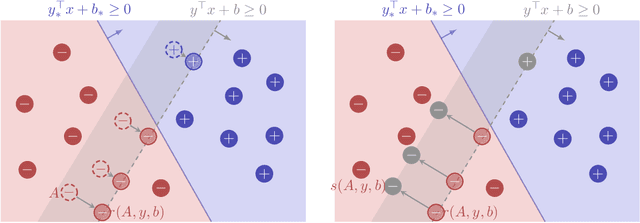
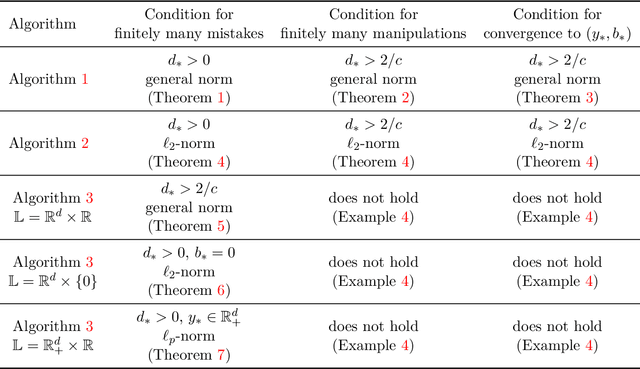
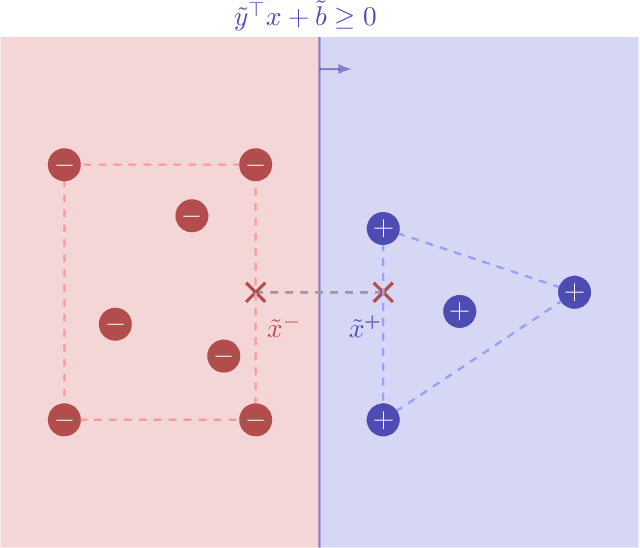
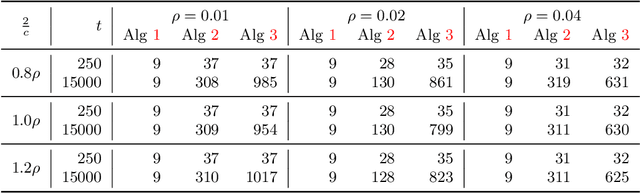
We consider an online strategic classification problem where each arriving agent can manipulate their true feature vector to obtain a positive predicted label, while incurring a cost that depends on the amount of manipulation. The learner seeks to predict the agent's true label given access to only the manipulated features. After the learner releases their prediction, the agent's true label is revealed. Previous algorithms such as the strategic perceptron guarantee finitely many mistakes under a margin assumption on agents' true feature vectors. However, these are not guaranteed to encourage agents to be truthful. Promoting truthfulness is intimately linked to obtaining adequate margin on the predictions, thus we provide two new algorithms aimed at recovering the maximum margin classifier in the presence of strategic agent behavior. We prove convergence, finite mistake and finite manipulation guarantees for a variety of agent cost structures. We also provide generalized versions of the strategic perceptron with mistake guarantees for different costs. Our numerical study on real and synthetic data demonstrates that the new algorithms outperform previous ones in terms of margin, number of manipulation and number of mistakes.

Projection-Free Online Convex Optimization with Stochastic Constraints

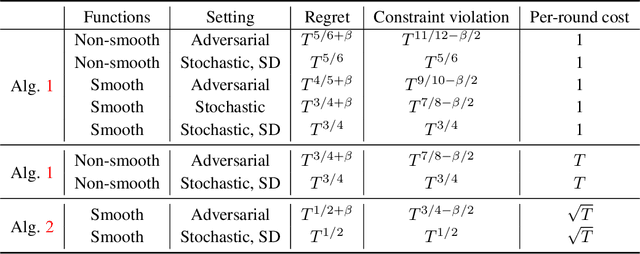
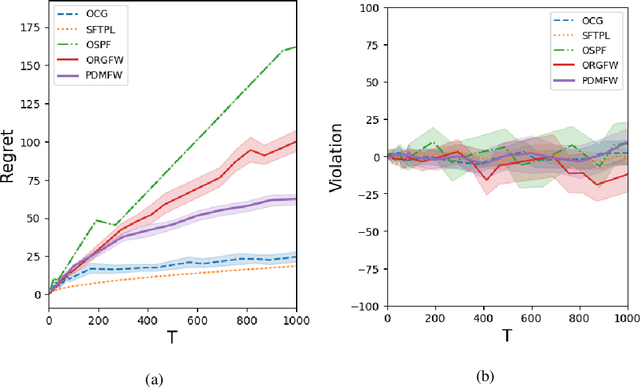
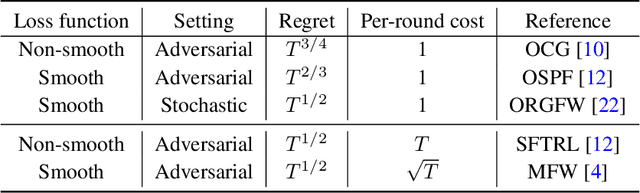
This paper develops projection-free algorithms for online convex optimization with stochastic constraints. We design an online primal-dual projection-free framework that can take any projection-free algorithms developed for online convex optimization with no long-term constraint. With this general template, we deduce sublinear regret and constraint violation bounds for various settings. Moreover, for the case where the loss and constraint functions are smooth, we develop a primal-dual conditional gradient method that achieves $O(\sqrt{T})$ regret and $O(T^{3/4})$ constraint violations. Furthermore, for the setting where the loss and constraint functions are stochastic and strong duality holds for the associated offline stochastic optimization problem, we prove that the constraint violation can be reduced to have the same asymptotic growth as the regret.

Risk Guarantees for End-to-End Prediction and Optimization Processes

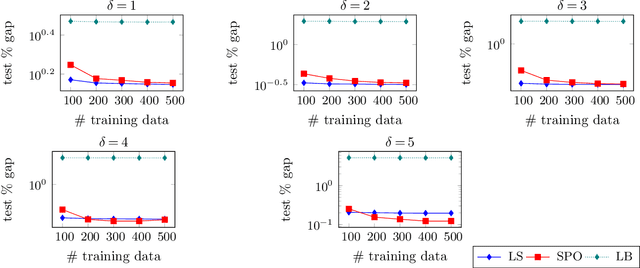
Prediction models are often employed in estimating parameters of optimization models. Despite the fact that in an end-to-end view, the real goal is to achieve good optimization performance, the prediction performance is measured on its own. While it is usually believed that good prediction performance in estimating the parameters will result in good subsequent optimization performance, formal theoretical guarantees on this are notably lacking. In this paper, we explore conditions that allow us to explicitly describe how the prediction performance governs the optimization performance. Our weaker condition allows for an asymptotic convergence result, while our stronger condition allows for exact quantification of the optimization performance in terms of the prediction performance. In general, verification of these conditions is a non-trivial task. Nevertheless, we show that our weaker condition is equivalent to the well-known Fisher consistency concept from the learning theory literature. This then allows us to easily check our weaker condition for several loss functions. We also establish that the squared error loss function satisfies our stronger condition. Consequently, we derive the exact theoretical relationship between prediction performance measured with the squared loss, as well as a class of symmetric loss functions, and the subsequent optimization performance. In a computational study on portfolio optimization, fractional knapsack and multiclass classification problems, we compare the optimization performance of using of several prediction loss functions (some that are Fisher consistent and some that are not) and demonstrate that lack of consistency of the loss function can indeed have a detrimental effect on performance.

Adversarial Classification via Distributional Robustness with Wasserstein Ambiguity

We study a model for adversarial classification based on distributionally robust chance constraints. We show that under Wasserstein ambiguity, the model aims to minimize the conditional value-at-risk of the distance to misclassification, and we explore links to previous adversarial classification models and maximum margin classifiers. We also provide a reformulation of the distributionally robust model for linear classifiers, and show it is equivalent to minimizing a regularized ramp loss. Numerical experiments show that, despite the nonconvexity, standard descent methods appear to converge to the global minimizer for this problem. Inspired by this observation, we show that, for a certain benign distribution, the regularized ramp loss minimization problem has a single stationary point, at the global minimizer.