Mistake, Manipulation and Margin Guarantees in Online Strategic Classification

We consider an online strategic classification problem where each arriving agent can manipulate their true feature vector to obtain a positive predicted label, while incurring a cost that depends on the amount of manipulation. The learner seeks to predict the agent's true label given access to only the manipulated features. After the learner releases their prediction, the agent's true label is revealed. Previous algorithms such as the strategic perceptron guarantee finitely many mistakes under a margin assumption on agents' true feature vectors. However, these are not guaranteed to encourage agents to be truthful. Promoting truthfulness is intimately linked to obtaining adequate margin on the predictions, thus we provide two new algorithms aimed at recovering the maximum margin classifier in the presence of strategic agent behavior. We prove convergence, finite mistake and finite manipulation guarantees for a variety of agent cost structures. We also provide generalized versions of the strategic perceptron with mistake guarantees for different costs. Our numerical study on real and synthetic data demonstrates that the new algorithms outperform previous ones in terms of margin, number of manipulation and number of mistakes.

A Field Test of Bandit Algorithms for Recommendations: Understanding the Validity of Assumptions on Human Preferences in Multi-armed Bandits

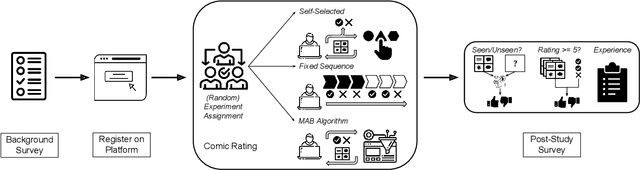
Personalized recommender systems suffuse modern life, shaping what media we read and what products we consume. Algorithms powering such systems tend to consist of supervised learning-based heuristics, such as latent factor models with a variety of heuristically chosen prediction targets. Meanwhile, theoretical treatments of recommendation frequently address the decision-theoretic nature of the problem, including the need to balance exploration and exploitation, via the multi-armed bandits (MABs) framework. However, MAB-based approaches rely heavily on assumptions about human preferences. These preference assumptions are seldom tested using human subject studies, partly due to the lack of publicly available toolkits to conduct such studies. In this work, we conduct a study with crowdworkers in a comics recommendation MABs setting. Each arm represents a comic category, and users provide feedback after each recommendation. We check the validity of core MABs assumptions-that human preferences (reward distributions) are fixed over time-and find that they do not hold. This finding suggests that any MAB algorithm used for recommender systems should account for human preference dynamics. While answering these questions, we provide a flexible experimental framework for understanding human preference dynamics and testing MABs algorithms with human users. The code for our experimental framework and the collected data can be found at https://github.com/HumainLab/human-bandit-evaluation.

Constrained Optimization of Rank-One Functions with Indicator Variables

Optimization problems involving minimization of a rank-one convex function over constraints modeling restrictions on the support of the decision variables emerge in various machine learning applications. These problems are often modeled with indicator variables for identifying the support of the continuous variables. In this paper we investigate compact extended formulations for such problems through perspective reformulation techniques. In contrast to the majority of previous work that relies on support function arguments and disjunctive programming techniques to provide convex hull results, we propose a constructive approach that exploits a hidden conic structure induced by perspective functions. To this end, we first establish a convex hull result for a general conic mixed-binary set in which each conic constraint involves a linear function of independent continuous variables and a set of binary variables. We then demonstrate that extended representations of sets associated with epigraphs of rank-one convex functions over constraints modeling indicator relations naturally admit such a conic representation. This enables us to systematically give perspective formulations for the convex hull descriptions of these sets with nonlinear separable or non-separable objective functions, sign constraints on continuous variables, and combinatorial constraints on indicator variables. We illustrate the efficacy of our results on sparse nonnegative logistic regression problems.

Risk Guarantees for End-to-End Prediction and Optimization Processes

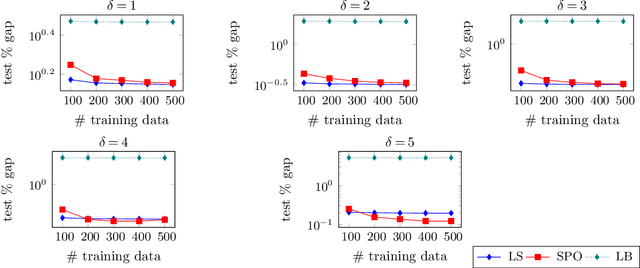
Prediction models are often employed in estimating parameters of optimization models. Despite the fact that in an end-to-end view, the real goal is to achieve good optimization performance, the prediction performance is measured on its own. While it is usually believed that good prediction performance in estimating the parameters will result in good subsequent optimization performance, formal theoretical guarantees on this are notably lacking. In this paper, we explore conditions that allow us to explicitly describe how the prediction performance governs the optimization performance. Our weaker condition allows for an asymptotic convergence result, while our stronger condition allows for exact quantification of the optimization performance in terms of the prediction performance. In general, verification of these conditions is a non-trivial task. Nevertheless, we show that our weaker condition is equivalent to the well-known Fisher consistency concept from the learning theory literature. This then allows us to easily check our weaker condition for several loss functions. We also establish that the squared error loss function satisfies our stronger condition. Consequently, we derive the exact theoretical relationship between prediction performance measured with the squared loss, as well as a class of symmetric loss functions, and the subsequent optimization performance. In a computational study on portfolio optimization, fractional knapsack and multiclass classification problems, we compare the optimization performance of using of several prediction loss functions (some that are Fisher consistent and some that are not) and demonstrate that lack of consistency of the loss function can indeed have a detrimental effect on performance.

Online Convex Optimization Perspective for Learning from Dynamically Revealed Preferences

We study the problem of online learning (OL) from revealed preferences: a learner wishes to learn an agent's private utility function through observing the agent's utility-maximizing actions in a changing environment. We adopt an online inverse optimization setup, where the learner observes a stream of agent's actions in an online fashion and the learning performance is measured by regret associated with a loss function. Due to the inverse optimization component, attaining or proving convexity is difficult for all of the usual loss functions in the literature. We address this challenge by designing a new loss function that is convex under relatively mild assumptions. Moreover, we establish that the regret with respect to our new loss function also bounds the regret with respect to all other usual loss functions. This then allows us to design a flexible OL framework that enables a unified treatment of loss functions and supports a variety of online convex optimization algorithms. We demonstrate with theoretical and empirical evidence that our framework based on the new loss function (in particular online Mirror Descent) has significant advantages in terms of eliminating technical assumptions as well as regret performance and solution time over other OL algorithms from the literature.