A Field Test of Bandit Algorithms for Recommendations: Understanding the Validity of Assumptions on Human Preferences in Multi-armed Bandits

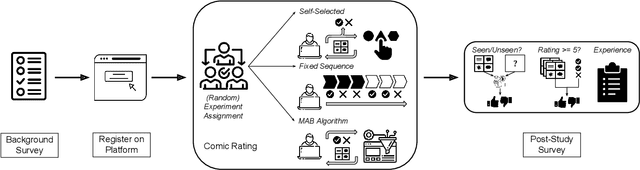
Personalized recommender systems suffuse modern life, shaping what media we read and what products we consume. Algorithms powering such systems tend to consist of supervised learning-based heuristics, such as latent factor models with a variety of heuristically chosen prediction targets. Meanwhile, theoretical treatments of recommendation frequently address the decision-theoretic nature of the problem, including the need to balance exploration and exploitation, via the multi-armed bandits (MABs) framework. However, MAB-based approaches rely heavily on assumptions about human preferences. These preference assumptions are seldom tested using human subject studies, partly due to the lack of publicly available toolkits to conduct such studies. In this work, we conduct a study with crowdworkers in a comics recommendation MABs setting. Each arm represents a comic category, and users provide feedback after each recommendation. We check the validity of core MABs assumptions-that human preferences (reward distributions) are fixed over time-and find that they do not hold. This finding suggests that any MAB algorithm used for recommender systems should account for human preference dynamics. While answering these questions, we provide a flexible experimental framework for understanding human preference dynamics and testing MABs algorithms with human users. The code for our experimental framework and the collected data can be found at https://github.com/HumainLab/human-bandit-evaluation.

Rebounding Bandits for Modeling Satiation Effects

Psychological research shows that enjoyment of many goods is subject to satiation, with enjoyment declining after repeated exposures to the same item. Nevertheless, proposed algorithms for powering recommender systems seldom model these dynamics, instead proceeding as though user preferences were fixed in time. In this work, we adopt a multi-armed bandit setup, modeling satiation dynamics as a time-invariant linear dynamical system. In our model, the expected rewards for each arm decline monotonically with consecutive exposures and rebound towards the initial reward whenever that arm is not pulled. We analyze this model, showing that, when the arms exhibit deterministic identical dynamics, our problem is equivalent to a specific instance of Max K-Cut. In this case, a greedy policy, which plays the arms in a cyclic order, is optimal. In the general setting, where each arm's satiation dynamics are stochastic and governed by different (unknown) parameters, we propose an algorithm that first uses offline data to estimate each arm's reward model and then plans using a generalization of the greedy policy.