Stochastic Gradient Methods with Preconditioned Updates

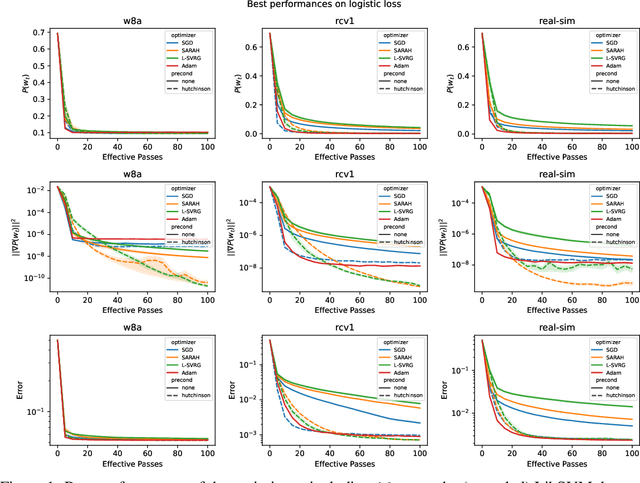
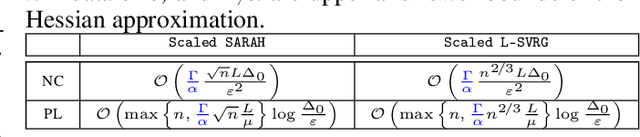
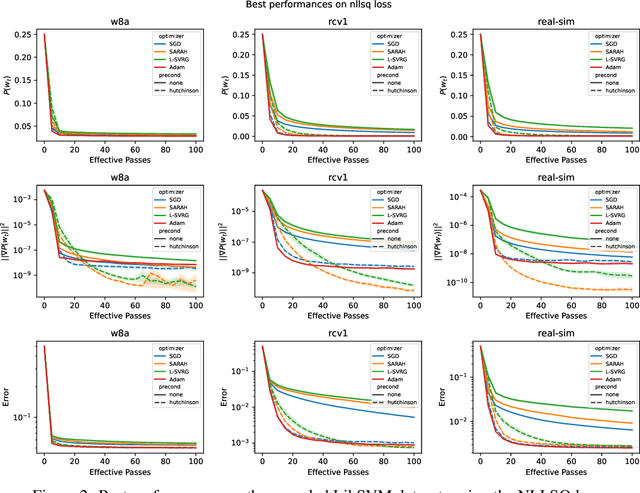
This work considers non-convex finite sum minimization. There are a number of algorithms for such problems, but existing methods often work poorly when the problem is badly scaled and/or ill-conditioned, and a primary goal of this work is to introduce methods that alleviate this issue. Thus, here we include a preconditioner that is based upon Hutchinson's approach to approximating the diagonal of the Hessian, and couple it with several gradient based methods to give new `scaled' algorithms: {\tt Scaled SARAH} and {\tt Scaled L-SVRG}. Theoretical complexity guarantees under smoothness assumptions are presented, and we prove linear convergence when both smoothness and the PL-condition is assumed. Because our adaptively scaled methods use approximate partial second order curvature information, they are better able to mitigate the impact of badly scaled problems, and this improved practical performance is demonstrated in the numerical experiments that are also presented in this work.