Collaborative and Efficient Personalization with Mixtures of Adaptors

Non-iid data is prevalent in real-world federated learning problems. Data heterogeneity can come in different types in terms of distribution shifts. In this work, we are interested in the heterogeneity that comes from concept shifts, i.e., shifts in the prediction across clients. In particular, we consider multi-task learning, where we want the model to adapt to the task of the client. We propose a parameter-efficient framework to tackle this issue, where each client learns to mix between parameter-efficient adaptors according to its task. We use Low-Rank Adaptors (LoRAs) as the backbone and extend its concept to other types of layers. We call our framework Federated Low-Rank Adaptive Learning (FLoRAL). This framework is not an algorithm but rather a model parameterization for a multi-task learning objective, so it can work on top of any algorithm that optimizes this objective, which includes many algorithms from the literature. FLoRAL is memory-efficient, and clients are personalized with small states (e.g., one number per adaptor) as the adaptors themselves are federated. Hence, personalization is--in this sense--federated as well. Even though clients can personalize more freely by training an adaptor locally, we show that collaborative and efficient training of adaptors is possible and performs better. We also show that FLoRAL can outperform an ensemble of full models with optimal cluster assignment, which demonstrates the benefits of federated personalization and the robustness of FLoRAL to overfitting. We show promising experimental results on synthetic datasets, real-world federated multi-task problems such as MNIST, CIFAR-10, and CIFAR-100. We also provide a theoretical analysis of local SGD on a relaxed objective and discuss the effects of aggregation mismatch on convergence.

Byzantine-Tolerant Methods for Distributed Variational Inequalities

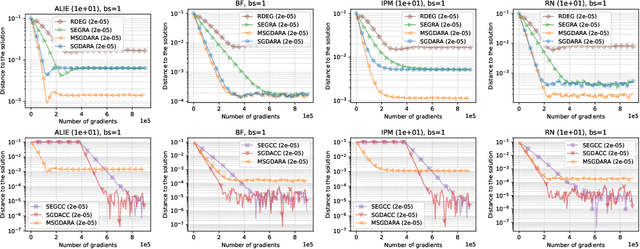
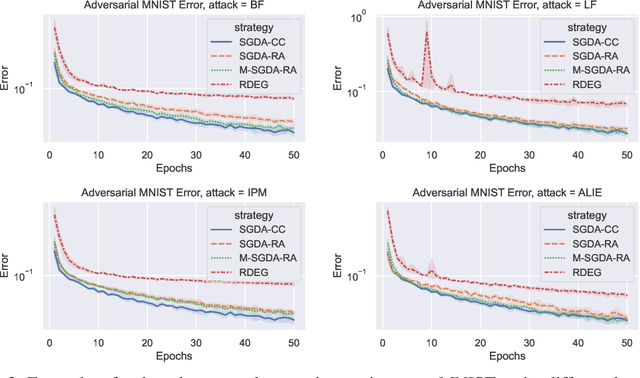
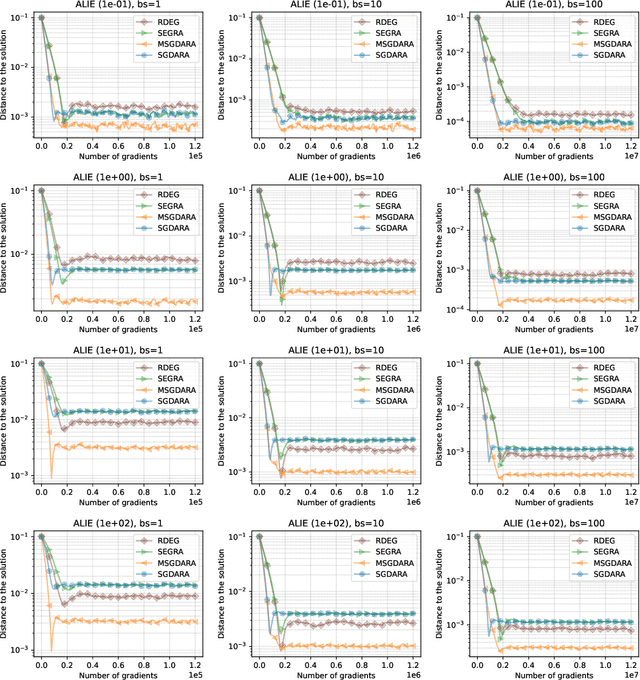
Robustness to Byzantine attacks is a necessity for various distributed training scenarios. When the training reduces to the process of solving a minimization problem, Byzantine robustness is relatively well-understood. However, other problem formulations, such as min-max problems or, more generally, variational inequalities, arise in many modern machine learning and, in particular, distributed learning tasks. These problems significantly differ from the standard minimization ones and, therefore, require separate consideration. Nevertheless, only one work (Adibi et al., 2022) addresses this important question in the context of Byzantine robustness. Our work makes a further step in this direction by providing several (provably) Byzantine-robust methods for distributed variational inequality, thoroughly studying their theoretical convergence, removing the limitations of the previous work, and providing numerical comparisons supporting the theoretical findings.

Partial Disentanglement with Partially-Federated GANs (PaDPaF)

Federated learning has become a popular machine learning paradigm with many potential real-life applications, including recommendation systems, the Internet of Things (IoT), healthcare, and self-driving cars. Though most current applications focus on classification-based tasks, learning personalized generative models remains largely unexplored, and their benefits in the heterogeneous setting still need to be better understood. This work proposes a novel architecture combining global client-agnostic and local client-specific generative models. We show that using standard techniques for training federated models, our proposed model achieves privacy and personalization that is achieved by implicitly disentangling the globally-consistent representation (i.e. content) from the client-dependent variations (i.e. style). Using such decomposition, personalized models can generate locally unseen labels while preserving the given style of the client and can predict the labels for all clients with high accuracy by training a simple linear classifier on the global content features. Furthermore, disentanglement enables other essential applications, such as data anonymization, by sharing only content. Extensive experimental evaluation corroborates our findings, and we also provide partial theoretical justifications for the proposed approach.

Stochastic Gradient Methods with Preconditioned Updates

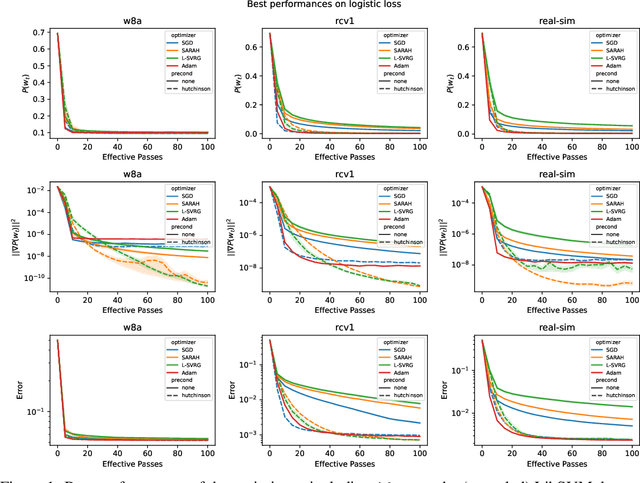
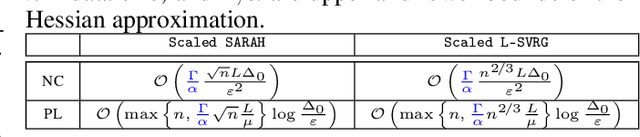
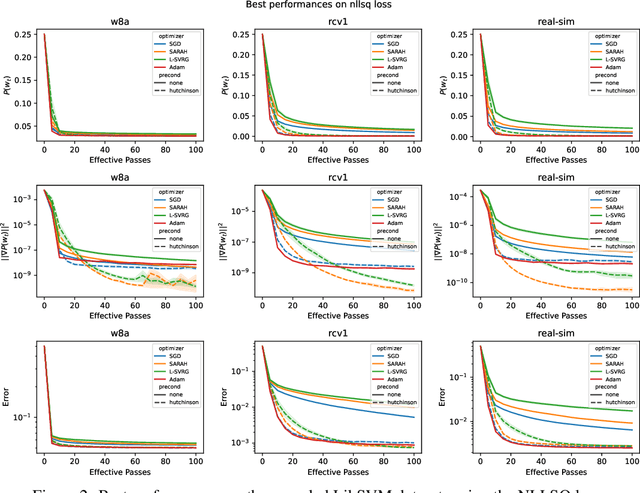
This work considers non-convex finite sum minimization. There are a number of algorithms for such problems, but existing methods often work poorly when the problem is badly scaled and/or ill-conditioned, and a primary goal of this work is to introduce methods that alleviate this issue. Thus, here we include a preconditioner that is based upon Hutchinson's approach to approximating the diagonal of the Hessian, and couple it with several gradient based methods to give new `scaled' algorithms: {\tt Scaled SARAH} and {\tt Scaled L-SVRG}. Theoretical complexity guarantees under smoothness assumptions are presented, and we prove linear convergence when both smoothness and the PL-condition is assumed. Because our adaptively scaled methods use approximate partial second order curvature information, they are better able to mitigate the impact of badly scaled problems, and this improved practical performance is demonstrated in the numerical experiments that are also presented in this work.