AdaBatchGrad: Combining Adaptive Batch Size and Adaptive Step Size

This paper presents a novel adaptation of the Stochastic Gradient Descent (SGD), termed AdaBatchGrad. This modification seamlessly integrates an adaptive step size with an adjustable batch size. An increase in batch size and a decrease in step size are well-known techniques to tighten the area of convergence of SGD and decrease its variance. A range of studies by R. Byrd and J. Nocedal introduced various testing techniques to assess the quality of mini-batch gradient approximations and choose the appropriate batch sizes at every step. Methods that utilized exact tests were observed to converge within $O(LR^2/\varepsilon)$ iterations. Conversely, inexact test implementations sometimes resulted in non-convergence and erratic performance. To address these challenges, AdaBatchGrad incorporates both adaptive batch and step sizes, enhancing the method's robustness and stability. For exact tests, our approach converges in $O(LR^2/\varepsilon)$ iterations, analogous to standard gradient descent. For inexact tests, it achieves convergence in $O(\max\lbrace LR^2/\varepsilon, \sigma^2 R^2/\varepsilon^2 \rbrace )$ iterations. This makes AdaBatchGrad markedly more robust and computationally efficient relative to prevailing methods. To substantiate the efficacy of our method, we experimentally show, how the introduction of adaptive step size and adaptive batch size gradually improves the performance of regular SGD. The results imply that AdaBatchGrad surpasses alternative methods, especially when applied to inexact tests.

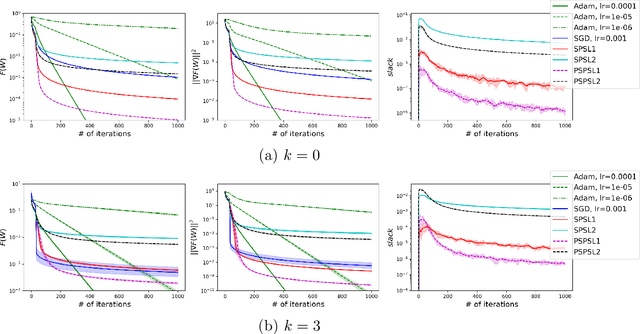
SANIA: Polyak-type Optimization Framework Leads to Scale Invariant Stochastic Algorithms

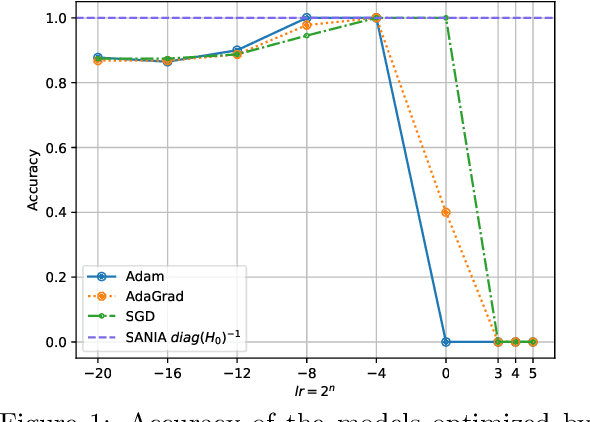
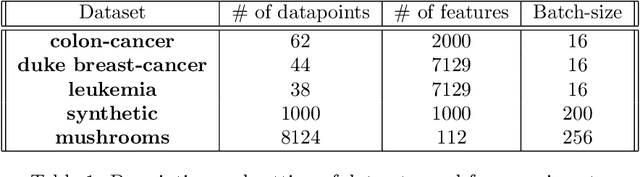
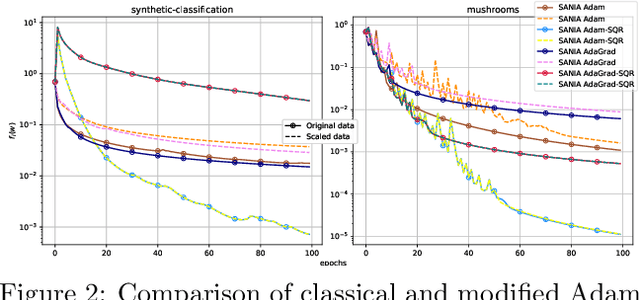
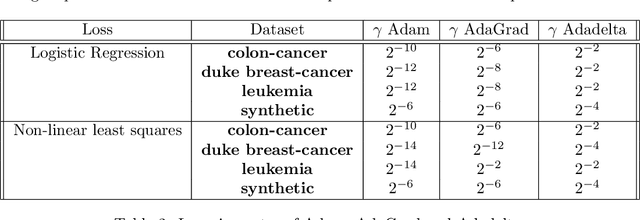
Adaptive optimization methods are widely recognized as among the most popular approaches for training Deep Neural Networks (DNNs). Techniques such as Adam, AdaGrad, and AdaHessian utilize a preconditioner that modifies the search direction by incorporating information about the curvature of the objective function. However, despite their adaptive characteristics, these methods still require manual fine-tuning of the step-size. This, in turn, impacts the time required to solve a particular problem. This paper presents an optimization framework named SANIA to tackle these challenges. Beyond eliminating the need for manual step-size hyperparameter settings, SANIA incorporates techniques to address poorly scaled or ill-conditioned problems. We also explore several preconditioning methods, including Hutchinson's method, which approximates the Hessian diagonal of the loss function. We conclude with an extensive empirical examination of the proposed techniques across classification tasks, covering both convex and non-convex contexts.

Stochastic Gradient Descent with Preconditioned Polyak Step-size

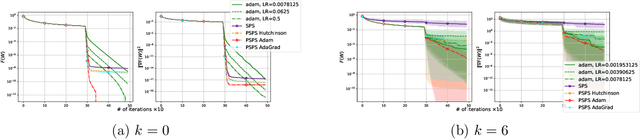
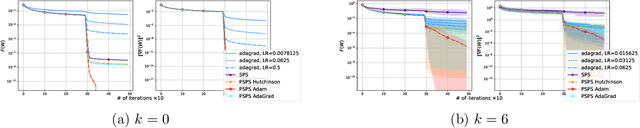
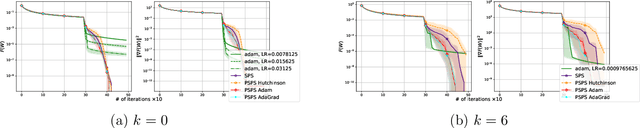
Stochastic Gradient Descent (SGD) is one of the many iterative optimization methods that are widely used in solving machine learning problems. These methods display valuable properties and attract researchers and industrial machine learning engineers with their simplicity. However, one of the weaknesses of this type of methods is the necessity to tune learning rate (step-size) for every loss function and dataset combination to solve an optimization problem and get an efficient performance in a given time budget. Stochastic Gradient Descent with Polyak Step-size (SPS) is a method that offers an update rule that alleviates the need of fine-tuning the learning rate of an optimizer. In this paper, we propose an extension of SPS that employs preconditioning techniques, such as Hutchinson's method, Adam, and AdaGrad, to improve its performance on badly scaled and/or ill-conditioned datasets.