Clipped Stochastic Methods for Variational Inequalities with Heavy-Tailed Noise

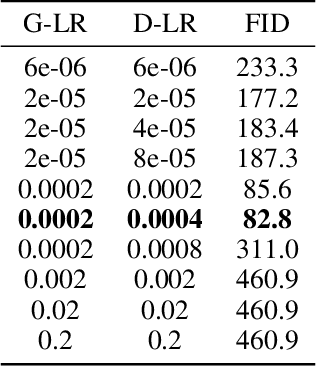
Stochastic first-order methods such as Stochastic Extragradient (SEG) or Stochastic Gradient Descent-Ascent (SGDA) for solving smooth minimax problems and, more generally, variational inequality problems (VIP) have been gaining a lot of attention in recent years due to the growing popularity of adversarial formulations in machine learning. However, while high-probability convergence bounds are known to reflect the actual behavior of stochastic methods more accurately, most convergence results are provided in expectation. Moreover, the only known high-probability complexity results have been derived under restrictive sub-Gaussian (light-tailed) noise and bounded domain Assump. [Juditsky et al., 2011]. In this work, we prove the first high-probability complexity results with logarithmic dependence on the confidence level for stochastic methods for solving monotone and structured non-monotone VIPs with non-sub-Gaussian (heavy-tailed) noise and unbounded domains. In the monotone case, our results match the best-known ones in the light-tails case [Juditsky et al., 2011], and are novel for structured non-monotone problems such as negative comonotone, quasi-strongly monotone, and/or star-cocoercive ones. We achieve these results by studying SEG and SGDA with clipping. In addition, we numerically validate that the gradient noise of many practical GAN formulations is heavy-tailed and show that clipping improves the performance of SEG/SGDA.