Better LMO-based Momentum Methods with Second-Order Information

The use of momentum in stochastic optimization algorithms has shown empirical success across a range of machine learning tasks. Recently, a new class of stochastic momentum algorithms has emerged within the Linear Minimization Oracle (LMO) framework--leading to state-of-the-art methods, such as Muon, Scion, and Gluon, that effectively solve deep neural network training problems. However, traditional stochastic momentum methods offer convergence guarantees no better than the ${O}(1/K^{1/4})$ rate. While several approaches--such as Hessian-Corrected Momentum (HCM)--have aimed to improve this rate, their theoretical results are generally restricted to the Euclidean norm setting. This limitation hinders their applicability in problems, where arbitrary norms are often required. In this paper, we extend the LMO-based framework by integrating HCM, and provide convergence guarantees under relaxed smoothness and arbitrary norm settings. We establish improved convergence rates of ${O}(1/K^{1/3})$ for HCM, which can adapt to the geometry of the problem and achieve a faster rate than traditional momentum. Experimental results on training Multi-Layer Perceptrons (MLPs) and Long Short-Term Memory (LSTM) networks verify our theoretical observations.

Improved Convergence in Parameter-Agnostic Error Feedback through Momentum

Communication compression is essential for scalable distributed training of modern machine learning models, but it often degrades convergence due to the noise it introduces. Error Feedback (EF) mechanisms are widely adopted to mitigate this issue of distributed compression algorithms. Despite their popularity and training efficiency, existing distributed EF algorithms often require prior knowledge of problem parameters (e.g., smoothness constants) to fine-tune stepsizes. This limits their practical applicability especially in large-scale neural network training. In this paper, we study normalized error feedback algorithms that combine EF with normalized updates, various momentum variants, and parameter-agnostic, time-varying stepsizes, thus eliminating the need for problem-dependent tuning. We analyze the convergence of these algorithms for minimizing smooth functions, and establish parameter-agnostic complexity bounds that are close to the best-known bounds with carefully-tuned problem-dependent stepsizes. Specifically, we show that normalized EF21 achieve the convergence rate of near ${O}(1/T^{1/4})$ for Polyak's heavy-ball momentum, ${O}(1/T^{2/7})$ for Iterative Gradient Transport (IGT), and ${O}(1/T^{1/3})$ for STORM and Hessian-corrected momentum. Our results hold with decreasing stepsizes and small mini-batches. Finally, our empirical experiments confirm our theoretical insights.

Methods with Local Steps and Random Reshuffling for Generally Smooth Non-Convex Federated Optimization

Non-convex Machine Learning problems typically do not adhere to the standard smoothness assumption. Based on empirical findings, Zhang et al. (2020b) proposed a more realistic generalized $(L_0, L_1)$-smoothness assumption, though it remains largely unexplored. Many existing algorithms designed for standard smooth problems need to be revised. However, in the context of Federated Learning, only a few works address this problem but rely on additional limiting assumptions. In this paper, we address this gap in the literature: we propose and analyze new methods with local steps, partial participation of clients, and Random Reshuffling without extra restrictive assumptions beyond generalized smoothness. The proposed methods are based on the proper interplay between clients' and server's stepsizes and gradient clipping. Furthermore, we perform the first analysis of these methods under the Polyak-{\L} ojasiewicz condition. Our theory is consistent with the known results for standard smooth problems, and our experimental results support the theoretical insights.

A Unified Theory of Stochastic Proximal Point Methods without Smoothness

This paper presents a comprehensive analysis of a broad range of variations of the stochastic proximal point method (SPPM). Proximal point methods have attracted considerable interest owing to their numerical stability and robustness against imperfect tuning, a trait not shared by the dominant stochastic gradient descent (SGD) algorithm. A framework of assumptions that we introduce encompasses methods employing techniques such as variance reduction and arbitrary sampling. A cornerstone of our general theoretical approach is a parametric assumption on the iterates, correction and control vectors. We establish a single theorem that ensures linear convergence under this assumption and the $\mu$-strong convexity of the loss function, and without the need to invoke smoothness. This integral theorem reinstates best known complexity and convergence guarantees for several existing methods which demonstrates the robustness of our approach. We expand our study by developing three new variants of SPPM, and through numerical experiments we elucidate various properties inherent to them.

Streamlining in the Riemannian Realm: Efficient Riemannian Optimization with Loopless Variance Reduction

In this study, we investigate stochastic optimization on Riemannian manifolds, focusing on the crucial variance reduction mechanism used in both Euclidean and Riemannian settings. Riemannian variance-reduced methods usually involve a double-loop structure, computing a full gradient at the start of each loop. Determining the optimal inner loop length is challenging in practice, as it depends on strong convexity or smoothness constants, which are often unknown or hard to estimate. Motivated by Euclidean methods, we introduce the Riemannian Loopless SVRG (R-LSVRG) and PAGE (R-PAGE) methods. These methods replace the outer loop with probabilistic gradient computation triggered by a coin flip in each iteration, ensuring simpler proofs, efficient hyperparameter selection, and sharp convergence guarantees. Using R-PAGE as a framework for non-convex Riemannian optimization, we demonstrate its applicability to various important settings. For example, we derive Riemannian MARINA (R-MARINA) for distributed settings with communication compression, providing the best theoretical communication complexity guarantees for non-convex distributed optimization over Riemannian manifolds. Experimental results support our theoretical findings.

Correlated Quantization for Faster Nonconvex Distributed Optimization

Quantization (Alistarh et al., 2017) is an important (stochastic) compression technique that reduces the volume of transmitted bits during each communication round in distributed model training. Suresh et al. (2022) introduce correlated quantizers and show their advantages over independent counterparts by analyzing distributed SGD communication complexity. We analyze the forefront distributed non-convex optimization algorithm MARINA (Gorbunov et al., 2022) utilizing the proposed correlated quantizers and show that it outperforms the original MARINA and distributed SGD of Suresh et al. (2022) with regard to the communication complexity. We significantly refine the original analysis of MARINA without any additional assumptions using the weighted Hessian variance (Tyurin et al., 2022), and then we expand the theoretical framework of MARINA to accommodate a substantially broader range of potentially correlated and biased compressors, thus dilating the applicability of the method beyond the conventional independent unbiased compressor setup. Extensive experimental results corroborate our theoretical findings.

MAST: Model-Agnostic Sparsified Training

We introduce a novel optimization problem formulation that departs from the conventional way of minimizing machine learning model loss as a black-box function. Unlike traditional formulations, the proposed approach explicitly incorporates an initially pre-trained model and random sketch operators, allowing for sparsification of both the model and gradient during training. We establish insightful properties of the proposed objective function and highlight its connections to the standard formulation. Furthermore, we present several variants of the Stochastic Gradient Descent (SGD) method adapted to the new problem formulation, including SGD with general sampling, a distributed version, and SGD with variance reduction techniques. We achieve tighter convergence rates and relax assumptions, bridging the gap between theoretical principles and practical applications, covering several important techniques such as Dropout and Sparse training. This work presents promising opportunities to enhance the theoretical understanding of model training through a sparsification-aware optimization approach.

A Guide Through the Zoo of Biased SGD

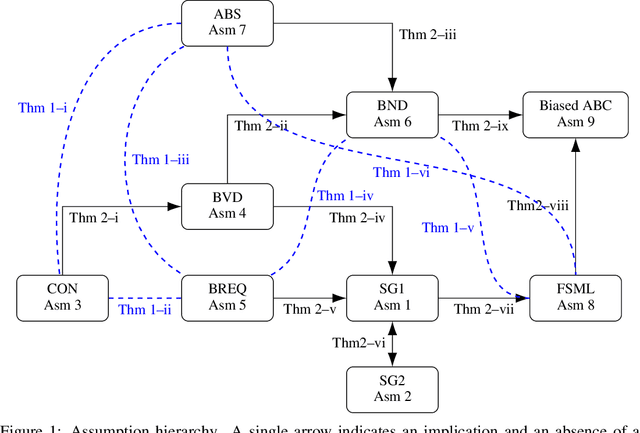
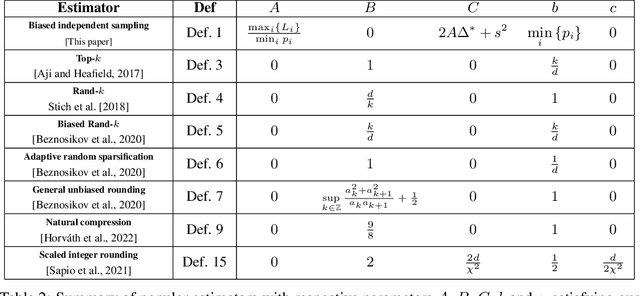
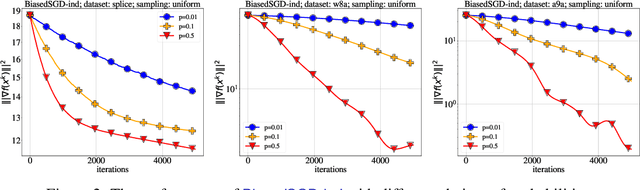
Stochastic Gradient Descent (SGD) is arguably the most important single algorithm in modern machine learning. Although SGD with unbiased gradient estimators has been studied extensively over at least half a century, SGD variants relying on biased estimators are rare. Nevertheless, there has been an increased interest in this topic in recent years. However, existing literature on SGD with biased estimators (BiasedSGD) lacks coherence since each new paper relies on a different set of assumptions, without any clear understanding of how they are connected, which may lead to confusion. We address this gap by establishing connections among the existing assumptions, and presenting a comprehensive map of the underlying relationships. Additionally, we introduce a new set of assumptions that is provably weaker than all previous assumptions, and use it to present a thorough analysis of BiasedSGD in both convex and non-convex settings, offering advantages over previous results. We also provide examples where biased estimators outperform their unbiased counterparts or where unbiased versions are simply not available. Finally, we demonstrate the effectiveness of our framework through experimental results that validate our theoretical findings.