Quartet II: Accurate LLM Pre-Training in NVFP4 by Improved Unbiased Gradient Estimation

The NVFP4 lower-precision format, supported in hardware by NVIDIA Blackwell GPUs, promises to allow, for the first time, end-to-end fully-quantized pre-training of massive models such as LLMs. Yet, existing quantized training methods still sacrifice some of the representation capacity of this format in favor of more accurate unbiased quantized gradient estimation by stochastic rounding (SR), losing noticeable accuracy relative to standard FP16 and FP8 training. In this paper, improve the state of the art for quantized training in NVFP4 via a novel unbiased quantization routine for micro-scaled formats, called MS-EDEN, that has more than 2x lower quantization error than SR. We integrate it into a novel fully-NVFP4 quantization scheme for linear layers, called Quartet II. We show analytically that Quartet II achieves consistently better gradient estimation across all major matrix multiplications, both on the forward and on the backward passes. In addition, our proposal synergizes well with recent training improvements aimed specifically at NVFP4. We further validate Quartet II on end-to-end LLM training with up to 1.9B parameters on 38B tokens. We provide kernels for execution on NVIDIA Blackwell GPUs with up to 4.2x speedup over BF16. Our code is available at https://github.com/IST-DASLab/Quartet-II .

Apertus: Democratizing Open and Compliant LLMs for Global Language Environments

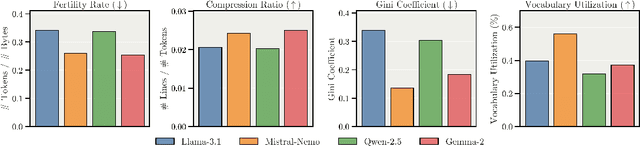
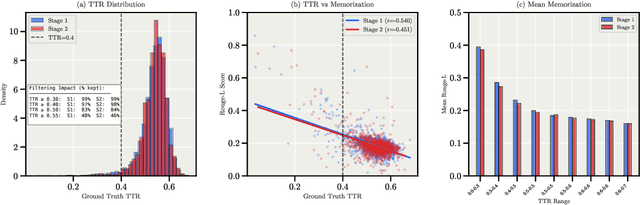
We present Apertus, a fully open suite of large language models (LLMs) designed to address two systemic shortcomings in today's open model ecosystem: data compliance and multilingual representation. Unlike many prior models that release weights without reproducible data pipelines or regard for content-owner rights, Apertus models are pretrained exclusively on openly available data, retroactively respecting robots.txt exclusions and filtering for non-permissive, toxic, and personally identifiable content. To mitigate risks of memorization, we adopt the Goldfish objective during pretraining, strongly suppressing verbatim recall of data while retaining downstream task performance. The Apertus models also expand multilingual coverage, training on 15T tokens from over 1800 languages, with ~40% of pretraining data allocated to non-English content. Released at 8B and 70B scales, Apertus approaches state-of-the-art results among fully open models on multilingual benchmarks, rivalling or surpassing open-weight counterparts. Beyond model weights, we release all scientific artifacts from our development cycle with a permissive license, including data preparation scripts, checkpoints, evaluation suites, and training code, enabling transparent audit and extension.

Quartet: Native FP4 Training Can Be Optimal for Large Language Models

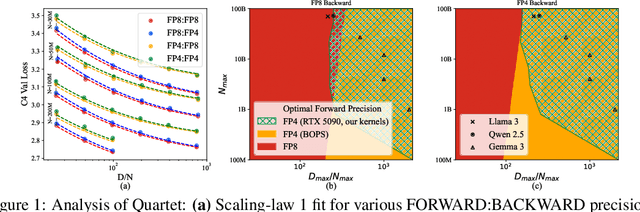
The rapid advancement of large language models (LLMs) has been paralleled by unprecedented increases in computational demands, with training costs for state-of-the-art models doubling every few months. Training models directly in low-precision arithmetic offers a solution, by improving both computational throughput and energy efficiency. Specifically, NVIDIA's recent Blackwell architecture facilitates extremely low-precision operations, specifically FP4 variants, promising substantial efficiency gains. Yet, current algorithms for training LLMs in FP4 precision face significant accuracy degradation and often rely on mixed-precision fallbacks. In this paper, we systematically investigate hardware-supported FP4 training and introduce Quartet, a new approach enabling accurate, end-to-end FP4 training with all the major computations (in e.g. linear layers) being performed in low precision. Through extensive evaluations on Llama-type models, we reveal a new low-precision scaling law that quantifies performance trade-offs across varying bit-widths and allows us to identify a "near-optimal" low-precision training technique in terms of accuracy-vs-computation, called Quartet. We implement Quartet using optimized CUDA kernels tailored for NVIDIA Blackwell GPUs, and show that it can achieve state-of-the-art accuracy for FP4 precision, successfully training billion-scale models. Our method demonstrates that fully FP4-based training is a competitive alternative to standard-precision and FP8 training. Our code is available at https://github.com/IST-DASLab/Quartet.

QuEST: Stable Training of LLMs with 1-Bit Weights and Activations

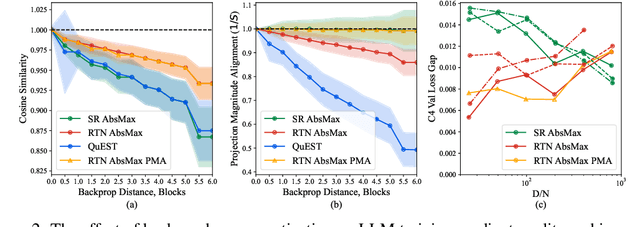
One approach to reducing the massive costs of large language models (LLMs) is the use of quantized or sparse representations for training or deployment. While post-training compression methods are very popular, the question of obtaining even more accurate compressed models by directly training over such representations, i.e., Quantization-Aware Training (QAT), is still open: for example, a recent study (arXiv:2411.04330v2) put the "optimal" bit-width at which models can be trained using QAT, while staying accuracy-competitive with standard FP16/BF16 precision, at 8-bits weights and activations. We advance this state-of-the-art via a new method called QuEST, which is Pareto-competitive with FP16, i.e., it provides better accuracy at lower model size, while training models with weights and activations in 4-bits or less. Moreover, QuEST allows stable training with 1-bit weights and activations. QuEST achieves this by improving two key aspects of QAT methods: (1) accurate and fast quantization of the (continuous) distributions of weights and activations via Hadamard normalization and MSE-optimal fitting; (2) a new trust gradient estimator based on the idea of explicitly minimizing the error between the noisy gradient computed over quantized states and the "true" (but unknown) full-precision gradient. Experiments on Llama-type architectures show that QuEST induces stable scaling laws across the entire range of hardware-supported precisions, and can be extended to sparse representations. We provide GPU kernel support showing that models produced by QuEST can be executed efficiently. Our code is available at https://github.com/IST-DASLab/QuEST.

Pushing the Limits of Large Language Model Quantization via the Linearity Theorem

Quantizing large language models has become a standard way to reduce their memory and computational costs. Typically, existing methods focus on breaking down the problem into individual layer-wise sub-problems, and minimizing per-layer error, measured via various metrics. Yet, this approach currently lacks theoretical justification and the metrics employed may be sub-optimal. In this paper, we present a "linearity theorem" establishing a direct relationship between the layer-wise $\ell_2$ reconstruction error and the model perplexity increase due to quantization. This insight enables two novel applications: (1) a simple data-free LLM quantization method using Hadamard rotations and MSE-optimal grids, dubbed HIGGS, which outperforms all prior data-free approaches such as the extremely popular NF4 quantized format, and (2) an optimal solution to the problem of finding non-uniform per-layer quantization levels which match a given compression constraint in the medium-bitwidth regime, obtained by reduction to dynamic programming. On the practical side, we demonstrate improved accuracy-compression trade-offs on Llama-3.1 and 3.2-family models, as well as on Qwen-family models. Further, we show that our method can be efficiently supported in terms of GPU kernels at various batch sizes, advancing both data-free and non-uniform quantization for LLMs.

Extreme Compression of Large Language Models via Additive Quantization

The emergence of accurate open large language models (LLMs) has led to a race towards quantization techniques for such models enabling execution on end-user devices. In this paper, we revisit the problem of "extreme" LLM compression--defined as targeting extremely low bit counts, such as 2 to 3 bits per parameter, from the point of view of classic methods in Multi-Codebook Quantization (MCQ). Our work builds on top of Additive Quantization, a classic algorithm from the MCQ family, and adapts it to the quantization of language models. The resulting algorithm advances the state-of-the-art in LLM compression, outperforming all recently-proposed techniques in terms of accuracy at a given compression budget. For instance, when compressing Llama 2 models to 2 bits per parameter, our algorithm quantizes the 7B model to 6.93 perplexity (a 1.29 improvement relative to the best prior work, and 1.81 points from FP16), the 13B model to 5.70 perplexity (a .36 improvement) and the 70B model to 3.94 perplexity (a .22 improvement) on WikiText2. We release our implementation of Additive Quantization for Language Models AQLM as a baseline to facilitate future research in LLM quantization.

Correlated Quantization for Faster Nonconvex Distributed Optimization

Quantization (Alistarh et al., 2017) is an important (stochastic) compression technique that reduces the volume of transmitted bits during each communication round in distributed model training. Suresh et al. (2022) introduce correlated quantizers and show their advantages over independent counterparts by analyzing distributed SGD communication complexity. We analyze the forefront distributed non-convex optimization algorithm MARINA (Gorbunov et al., 2022) utilizing the proposed correlated quantizers and show that it outperforms the original MARINA and distributed SGD of Suresh et al. (2022) with regard to the communication complexity. We significantly refine the original analysis of MARINA without any additional assumptions using the weighted Hessian variance (Tyurin et al., 2022), and then we expand the theoretical framework of MARINA to accommodate a substantially broader range of potentially correlated and biased compressors, thus dilating the applicability of the method beyond the conventional independent unbiased compressor setup. Extensive experimental results corroborate our theoretical findings.