Improved Convergence in Parameter-Agnostic Error Feedback through Momentum

Communication compression is essential for scalable distributed training of modern machine learning models, but it often degrades convergence due to the noise it introduces. Error Feedback (EF) mechanisms are widely adopted to mitigate this issue of distributed compression algorithms. Despite their popularity and training efficiency, existing distributed EF algorithms often require prior knowledge of problem parameters (e.g., smoothness constants) to fine-tune stepsizes. This limits their practical applicability especially in large-scale neural network training. In this paper, we study normalized error feedback algorithms that combine EF with normalized updates, various momentum variants, and parameter-agnostic, time-varying stepsizes, thus eliminating the need for problem-dependent tuning. We analyze the convergence of these algorithms for minimizing smooth functions, and establish parameter-agnostic complexity bounds that are close to the best-known bounds with carefully-tuned problem-dependent stepsizes. Specifically, we show that normalized EF21 achieve the convergence rate of near ${O}(1/T^{1/4})$ for Polyak's heavy-ball momentum, ${O}(1/T^{2/7})$ for Iterative Gradient Transport (IGT), and ${O}(1/T^{1/3})$ for STORM and Hessian-corrected momentum. Our results hold with decreasing stepsizes and small mini-batches. Finally, our empirical experiments confirm our theoretical insights.

MARINA-P: Superior Performance in Non-smooth Federated Optimization with Adaptive Stepsizes

Non-smooth communication-efficient federated optimization is crucial for many machine learning applications, yet remains largely unexplored theoretically. Recent advancements have primarily focused on smooth convex and non-convex regimes, leaving a significant gap in understanding the non-smooth convex setting. Additionally, existing literature often overlooks efficient server-to-worker communication (downlink), focusing primarily on worker-to-server communication (uplink). We consider a setup where uplink costs are negligible and focus on optimizing downlink communication by improving state-of-the-art schemes like EF21-P (arXiv:2209.15218) and MARINA-P (arXiv:2402.06412) in the non-smooth convex setting. We extend the non-smooth convex theory of EF21-P [Anonymous, 2024], originally developed for single-node scenarios, to the distributed setting, and extend MARINA-P to the non-smooth convex setting. For both algorithms, we prove an optimal $O(1/\sqrt{T})$ convergence rate and establish communication complexity bounds matching classical subgradient methods. We provide theoretical guarantees under constant, decreasing, and adaptive (Polyak-type) stepsizes. Our experiments demonstrate that MARINA-P with correlated compressors outperforms other methods in both smooth non-convex and non-smooth convex settings. This work presents the first theoretical results for distributed non-smooth optimization with server-to-worker compression, along with comprehensive analysis for various stepsize schemes.

Cohort Squeeze: Beyond a Single Communication Round per Cohort in Cross-Device Federated Learning

Virtually all federated learning (FL) methods, including FedAvg, operate in the following manner: i) an orchestrating server sends the current model parameters to a cohort of clients selected via certain rule, ii) these clients then independently perform a local training procedure (e.g., via SGD or Adam) using their own training data, and iii) the resulting models are shipped to the server for aggregation. This process is repeated until a model of suitable quality is found. A notable feature of these methods is that each cohort is involved in a single communication round with the server only. In this work we challenge this algorithmic design primitive and investigate whether it is possible to ``squeeze more juice" out of each cohort than what is possible in a single communication round. Surprisingly, we find that this is indeed the case, and our approach leads to up to 74% reduction in the total communication cost needed to train a FL model in the cross-device setting. Our method is based on a novel variant of the stochastic proximal point method (SPPM-AS) which supports a large collection of client sampling procedures some of which lead to further gains when compared to classical client selection approaches.

On machine learning analysis of atomic force microscopy images for image classification, sample surface recognition

Atomic force microscopy (AFM or SPM) imaging is one of the best matches with machine learning (ML) analysis among microscopy techniques. The digital format of AFM images allows for direct utilization in ML algorithms without the need for additional processing. Additionally, AFM enables the simultaneous imaging of distributions of over a dozen different physicochemical properties of sample surfaces, a process known as multidimensional imaging. While this wealth of information can be challenging to analyze using traditional methods, ML provides a seamless approach to this task. However, the relatively slow speed of AFM imaging poses a challenge in applying deep learning methods broadly used in image recognition. This Prospective is focused on ML recognition/classification when using a relatively small number of AFM images, small database. We discuss ML methods other than popular deep-learning neural networks. The described approach has already been successfully used to analyze and classify the surfaces of biological cells. It can be applied to recognize medical images, specific material processing, in forensic studies, even to identify the authenticity of arts. A general template for ML analysis specific to AFM is suggested, with a specific example of the identification of cell phenotype. Special attention is given to the analysis of the statistical significance of the obtained results, an important feature that is often overlooked in papers dealing with machine learning. A simple method for finding statistical significance is also described.

A Guide Through the Zoo of Biased SGD

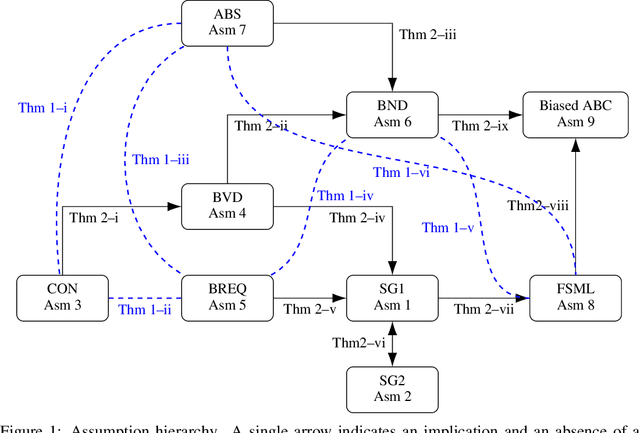
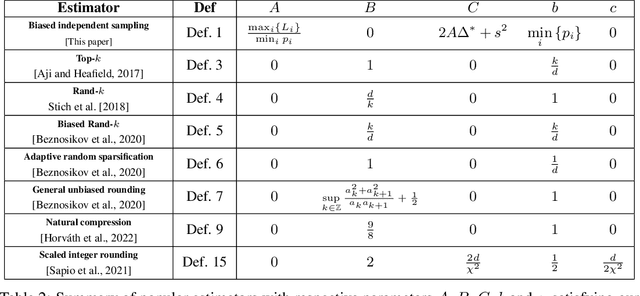
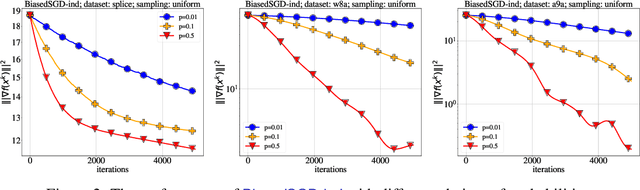
Stochastic Gradient Descent (SGD) is arguably the most important single algorithm in modern machine learning. Although SGD with unbiased gradient estimators has been studied extensively over at least half a century, SGD variants relying on biased estimators are rare. Nevertheless, there has been an increased interest in this topic in recent years. However, existing literature on SGD with biased estimators (BiasedSGD) lacks coherence since each new paper relies on a different set of assumptions, without any clear understanding of how they are connected, which may lead to confusion. We address this gap by establishing connections among the existing assumptions, and presenting a comprehensive map of the underlying relationships. Additionally, we introduce a new set of assumptions that is provably weaker than all previous assumptions, and use it to present a thorough analysis of BiasedSGD in both convex and non-convex settings, offering advantages over previous results. We also provide examples where biased estimators outperform their unbiased counterparts or where unbiased versions are simply not available. Finally, we demonstrate the effectiveness of our framework through experimental results that validate our theoretical findings.

Federated Optimization Algorithms with Random Reshuffling and Gradient Compression

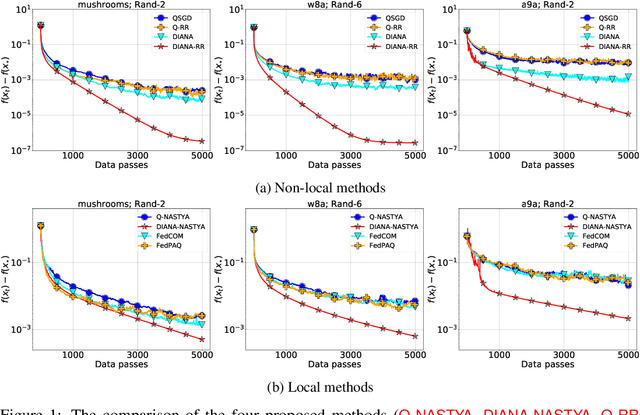
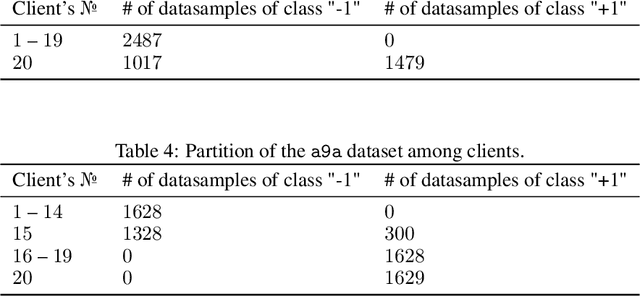
Gradient compression is a popular technique for improving communication complexity of stochastic first-order methods in distributed training of machine learning models. However, the existing works consider only with-replacement sampling of stochastic gradients. In contrast, it is well-known in practice and recently confirmed in theory that stochastic methods based on without-replacement sampling, e.g., Random Reshuffling (RR) method, perform better than ones that sample the gradients with-replacement. In this work, we close this gap in the literature and provide the first analysis of methods with gradient compression and without-replacement sampling. We first develop a distributed variant of random reshuffling with gradient compression (Q-RR), and show how to reduce the variance coming from gradient quantization through the use of control iterates. Next, to have a better fit to Federated Learning applications, we incorporate local computation and propose a variant of Q-RR called Q-NASTYA. Q-NASTYA uses local gradient steps and different local and global stepsizes. Next, we show how to reduce compression variance in this setting as well. Finally, we prove the convergence results for the proposed methods and outline several settings in which they improve upon existing algorithms.

3PC: Three Point Compressors for Communication-Efficient Distributed Training and a Better Theory for Lazy Aggregation

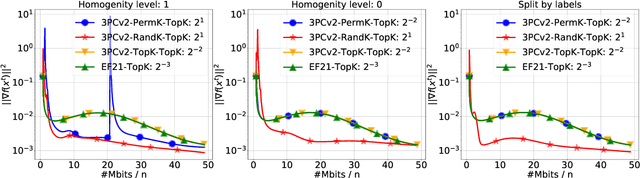
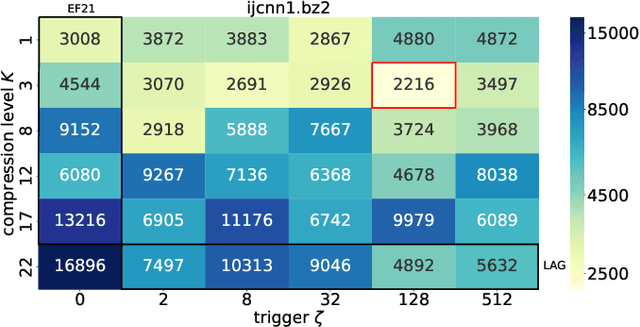
We propose and study a new class of gradient communication mechanisms for communication-efficient training -- three point compressors (3PC) -- as well as efficient distributed nonconvex optimization algorithms that can take advantage of them. Unlike most established approaches, which rely on a static compressor choice (e.g., Top-$K$), our class allows the compressors to {\em evolve} throughout the training process, with the aim of improving the theoretical communication complexity and practical efficiency of the underlying methods. We show that our general approach can recover the recently proposed state-of-the-art error feedback mechanism EF21 (Richt\'arik et al., 2021) and its theoretical properties as a special case, but also leads to a number of new efficient methods. Notably, our approach allows us to improve upon the state of the art in the algorithmic and theoretical foundations of the {\em lazy aggregation} literature (Chen et al., 2018). As a by-product that may be of independent interest, we provide a new and fundamental link between the lazy aggregation and error feedback literature. A special feature of our work is that we do not require the compressors to be unbiased.

EF21 with Bells & Whistles: Practical Algorithmic Extensions of Modern Error Feedback

First proposed by Seide (2014) as a heuristic, error feedback (EF) is a very popular mechanism for enforcing convergence of distributed gradient-based optimization methods enhanced with communication compression strategies based on the application of contractive compression operators. However, existing theory of EF relies on very strong assumptions (e.g., bounded gradients), and provides pessimistic convergence rates (e.g., while the best known rate for EF in the smooth nonconvex regime, and when full gradients are compressed, is $O(1/T^{2/3})$, the rate of gradient descent in the same regime is $O(1/T)$). Recently, Richt\'{a}rik et al. (2021) proposed a new error feedback mechanism, EF21, based on the construction of a Markov compressor induced by a contractive compressor. EF21 removes the aforementioned theoretical deficiencies of EF and at the same time works better in practice. In this work we propose six practical extensions of EF21, all supported by strong convergence theory: partial participation, stochastic approximation, variance reduction, proximal setting, momentum and bidirectional compression. Several of these techniques were never analyzed in conjunction with EF before, and in cases where they were (e.g., bidirectional compression), our rates are vastly superior.

EF21: A New, Simpler, Theoretically Better, and Practically Faster Error Feedback

Error feedback (EF), also known as error compensation, is an immensely popular convergence stabilization mechanism in the context of distributed training of supervised machine learning models enhanced by the use of contractive communication compression mechanisms, such as Top-$k$. First proposed by Seide et al (2014) as a heuristic, EF resisted any theoretical understanding until recently [Stich et al., 2018, Alistarh et al., 2018]. However, all existing analyses either i) apply to the single node setting only, ii) rely on very strong and often unreasonable assumptions, such global boundedness of the gradients, or iterate-dependent assumptions that cannot be checked a-priori and may not hold in practice, or iii) circumvent these issues via the introduction of additional unbiased compressors, which increase the communication cost. In this work we fix all these deficiencies by proposing and analyzing a new EF mechanism, which we call EF21, which consistently and substantially outperforms EF in practice. Our theoretical analysis relies on standard assumptions only, works in the distributed heterogeneous data setting, and leads to better and more meaningful rates. In particular, we prove that EF21 enjoys a fast $O(1/T)$ convergence rate for smooth nonconvex problems, beating the previous bound of $O(1/T^{2/3})$, which was shown a bounded gradients assumption. We further improve this to a fast linear rate for PL functions, which is the first linear convergence result for an EF-type method not relying on unbiased compressors. Since EF has a large number of applications where it reigns supreme, we believe that our 2021 variant, EF21, can a large impact on the practice of communication efficient distributed learning.