BurTorch: Revisiting Training from First Principles by Coupling Autodiff, Math Optimization, and Systems

In this work, we introduce BurTorch, a compact high-performance framework designed to optimize Deep Learning (DL) training on single-node workstations through an exceptionally efficient CPU-based backpropagation (Rumelhart et al., 1986; Linnainmaa, 1970) implementation. Although modern DL frameworks rely on compilerlike optimizations internally, BurTorch takes a different path. It adopts a minimalist design and demonstrates that, in these circumstances, classical compiled programming languages can play a significant role in DL research. By eliminating the overhead of large frameworks and making efficient implementation choices, BurTorch achieves orders-of-magnitude improvements in performance and memory efficiency when computing $\nabla f(x)$ on a CPU. BurTorch features a compact codebase designed to achieve two key goals simultaneously. First, it provides a user experience similar to script-based programming environments. Second, it dramatically minimizes runtime overheads. In large DL frameworks, the primary source of memory overhead for relatively small computation graphs $f(x)$ is due to feature-heavy implementations. We benchmarked BurTorch against widely used DL frameworks in their execution modes: JAX (Bradbury et al., 2018), PyTorch (Paszke et al., 2019), TensorFlow (Abadi et al., 2016); and several standalone libraries: Autograd (Maclaurin et al., 2015), Micrograd (Karpathy, 2020), Apple MLX (Hannun et al., 2023). For small compute graphs, BurTorch outperforms best-practice solutions by up to $\times 2000$ in runtime and reduces memory consumption by up to $\times 3500$. For a miniaturized GPT-3 model (Brown et al., 2020), BurTorch achieves up to a $\times 20$ speedup and reduces memory up to $\times 80$ compared to PyTorch.

Unlocking FedNL: Self-Contained Compute-Optimized Implementation

Federated Learning (FL) is an emerging paradigm that enables intelligent agents to collaboratively train Machine Learning (ML) models in a distributed manner, eliminating the need for sharing their local data. The recent work (arXiv:2106.02969) introduces a family of Federated Newton Learn (FedNL) algorithms, marking a significant step towards applying second-order methods to FL and large-scale optimization. However, the reference FedNL prototype exhibits three serious practical drawbacks: (i) It requires 4.8 hours to launch a single experiment in a sever-grade workstation; (ii) The prototype only simulates multi-node setting; (iii) Prototype integration into resource-constrained applications is challenging. To bridge the gap between theory and practice, we present a self-contained implementation of FedNL, FedNL-LS, FedNL-PP for single-node and multi-node settings. Our work resolves the aforementioned issues and reduces the wall clock time by x1000. With this FedNL outperforms alternatives for training logistic regression in a single-node -- CVXPY (arXiv:1603.00943), and in a multi-node -- Apache Spark (arXiv:1505.06807), Ray/Scikit-Learn (arXiv:1712.05889). Finally, we propose two practical-orientated compressors for FedNL - adaptive TopLEK and cache-aware RandSeqK, which fulfill the theory of FedNL.

PV-Tuning: Beyond Straight-Through Estimation for Extreme LLM Compression

There has been significant interest in "extreme" compression of large language models (LLMs), i.e., to 1-2 bits per parameter, which allows such models to be executed efficiently on resource-constrained devices. Existing work focused on improved one-shot quantization techniques and weight representations; yet, purely post-training approaches are reaching diminishing returns in terms of the accuracy-vs-bit-width trade-off. State-of-the-art quantization methods such as QuIP# and AQLM include fine-tuning (part of) the compressed parameters over a limited amount of calibration data; however, such fine-tuning techniques over compressed weights often make exclusive use of straight-through estimators (STE), whose performance is not well-understood in this setting. In this work, we question the use of STE for extreme LLM compression, showing that it can be sub-optimal, and perform a systematic study of quantization-aware fine-tuning strategies for LLMs. We propose PV-Tuning - a representation-agnostic framework that generalizes and improves upon existing fine-tuning strategies, and provides convergence guarantees in restricted cases. On the practical side, when used for 1-2 bit vector quantization, PV-Tuning outperforms prior techniques for highly-performant models such as Llama and Mistral. Using PV-Tuning, we achieve the first Pareto-optimal quantization for Llama 2 family models at 2 bits per parameter.

Error Feedback Reloaded: From Quadratic to Arithmetic Mean of Smoothness Constants

Error Feedback (EF) is a highly popular and immensely effective mechanism for fixing convergence issues which arise in distributed training methods (such as distributed GD or SGD) when these are enhanced with greedy communication compression techniques such as TopK. While EF was proposed almost a decade ago (Seide et al., 2014), and despite concentrated effort by the community to advance the theoretical understanding of this mechanism, there is still a lot to explore. In this work we study a modern form of error feedback called EF21 (Richtarik et al., 2021) which offers the currently best-known theoretical guarantees, under the weakest assumptions, and also works well in practice. In particular, while the theoretical communication complexity of EF21 depends on the quadratic mean of certain smoothness parameters, we improve this dependence to their arithmetic mean, which is always smaller, and can be substantially smaller, especially in heterogeneous data regimes. We take the reader on a journey of our discovery process. Starting with the idea of applying EF21 to an equivalent reformulation of the underlying problem which (unfortunately) requires (often impractical) machine cloning, we continue to the discovery of a new weighted version of EF21 which can (fortunately) be executed without any cloning, and finally circle back to an improved analysis of the original EF21 method. While this development applies to the simplest form of EF21, our approach naturally extends to more elaborate variants involving stochastic gradients and partial participation. Further, our technique improves the best-known theory of EF21 in the rare features regime (Richtarik et al., 2023). Finally, we validate our theoretical findings with suitable experiments.

Federated Learning is Better with Non-Homomorphic Encryption

Traditional AI methodologies necessitate centralized data collection, which becomes impractical when facing problems with network communication, data privacy, or storage capacity. Federated Learning (FL) offers a paradigm that empowers distributed AI model training without collecting raw data. There are different choices for providing privacy during FL training. One of the popular methodologies is employing Homomorphic Encryption (HE) - a breakthrough in privacy-preserving computation from Cryptography. However, these methods have a price in the form of extra computation and memory footprint. To resolve these issues, we propose an innovative framework that synergizes permutation-based compressors with Classical Cryptography, even though employing Classical Cryptography was assumed to be impossible in the past in the context of FL. Our framework offers a way to replace HE with cheaper Classical Cryptography primitives which provides security for the training process. It fosters asynchronous communication and provides flexible deployment options in various communication topologies.

Error Feedback Shines when Features are Rare

We provide the first proof that gradient descent $\left({\color{green}\sf GD}\right)$ with greedy sparsification $\left({\color{green}\sf TopK}\right)$ and error feedback $\left({\color{green}\sf EF}\right)$ can obtain better communication complexity than vanilla ${\color{green}\sf GD}$ when solving the distributed optimization problem $\min_{x\in \mathbb{R}^d} {f(x)=\frac{1}{n}\sum_{i=1}^n f_i(x)}$, where $n$ = # of clients, $d$ = # of features, and $f_1,\dots,f_n$ are smooth nonconvex functions. Despite intensive research since 2014 when ${\color{green}\sf EF}$ was first proposed by Seide et al., this problem remained open until now. We show that ${\color{green}\sf EF}$ shines in the regime when features are rare, i.e., when each feature is present in the data owned by a small number of clients only. To illustrate our main result, we show that in order to find a random vector $\hat{x}$ such that $\lVert {\nabla f(\hat{x})} \rVert^2 \leq \varepsilon$ in expectation, ${\color{green}\sf GD}$ with the ${\color{green}\sf Top1}$ sparsifier and ${\color{green}\sf EF}$ requires ${\cal O} \left(\left( L+{\color{blue}r} \sqrt{ \frac{{\color{red}c}}{n} \min \left( \frac{{\color{red}c}}{n} \max_i L_i^2, \frac{1}{n}\sum_{i=1}^n L_i^2 \right) }\right) \frac{1}{\varepsilon} \right)$ bits to be communicated by each worker to the server only, where $L$ is the smoothness constant of $f$, $L_i$ is the smoothness constant of $f_i$, ${\color{red}c}$ is the maximal number of clients owning any feature ($1\leq {\color{red}c} \leq n$), and ${\color{blue}r}$ is the maximal number of features owned by any client ($1\leq {\color{blue}r} \leq d$). Clearly, the communication complexity improves as ${\color{red}c}$ decreases (i.e., as features become more rare), and can be much better than the ${\cal O}({\color{blue}r} L \frac{1}{\varepsilon})$ communication complexity of ${\color{green}\sf GD}$ in the same regime.

Federated Learning with Regularized Client Participation

Federated Learning (FL) is a distributed machine learning approach where multiple clients work together to solve a machine learning task. One of the key challenges in FL is the issue of partial participation, which occurs when a large number of clients are involved in the training process. The traditional method to address this problem is randomly selecting a subset of clients at each communication round. In our research, we propose a new technique and design a novel regularized client participation scheme. Under this scheme, each client joins the learning process every $R$ communication rounds, which we refer to as a meta epoch. We have found that this participation scheme leads to a reduction in the variance caused by client sampling. Combined with the popular FedAvg algorithm (McMahan et al., 2017), it results in superior rates under standard assumptions. For instance, the optimization term in our main convergence bound decreases linearly with the product of the number of communication rounds and the size of the local dataset of each client, and the statistical term scales with step size quadratically instead of linearly (the case for client sampling with replacement), leading to better convergence rate $\mathcal{O}\left(\frac{1}{T^2}\right)$ compared to $\mathcal{O}\left(\frac{1}{T}\right)$, where $T$ is the total number of communication rounds. Furthermore, our results permit arbitrary client availability as long as each client is available for training once per each meta epoch.

Personalized Federated Learning with Communication Compression

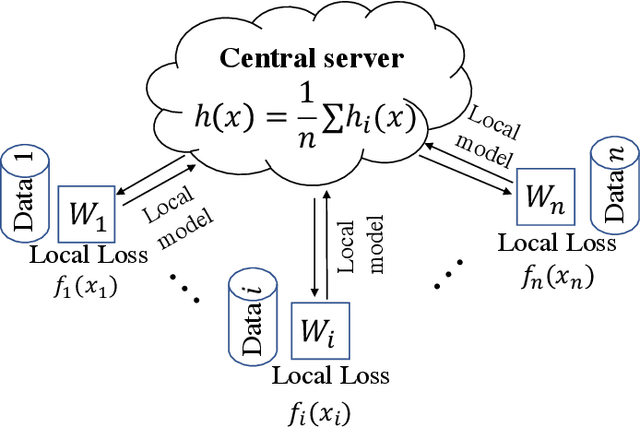
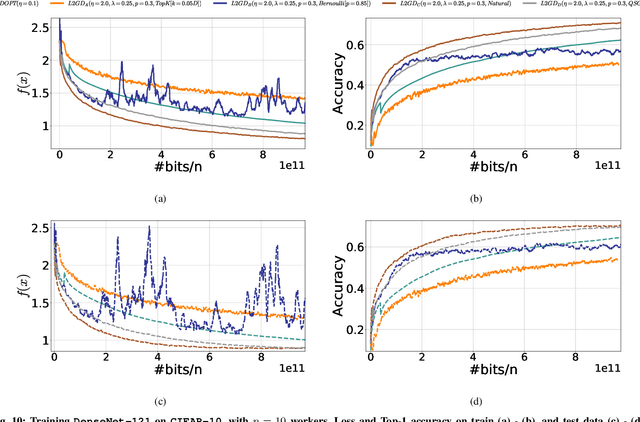
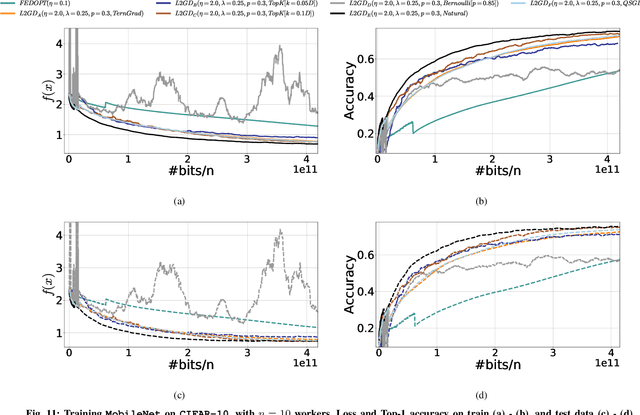
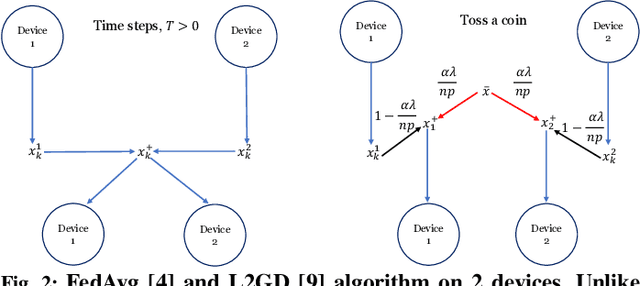
In contrast to training traditional machine learning (ML) models in data centers, federated learning (FL) trains ML models over local datasets contained on resource-constrained heterogeneous edge devices. Existing FL algorithms aim to learn a single global model for all participating devices, which may not be helpful to all devices participating in the training due to the heterogeneity of the data across the devices. Recently, Hanzely and Richt\'{a}rik (2020) proposed a new formulation for training personalized FL models aimed at balancing the trade-off between the traditional global model and the local models that could be trained by individual devices using their private data only. They derived a new algorithm, called Loopless Gradient Descent (L2GD), to solve it and showed that this algorithms leads to improved communication complexity guarantees in regimes when more personalization is required. In this paper, we equip their L2GD algorithm with a bidirectional compression mechanism to further reduce the communication bottleneck between the local devices and the server. Unlike other compression-based algorithms used in the FL-setting, our compressed L2GD algorithm operates on a probabilistic communication protocol, where communication does not happen on a fixed schedule. Moreover, our compressed L2GD algorithm maintains a similar convergence rate as vanilla SGD without compression. To empirically validate the efficiency of our algorithm, we perform diverse numerical experiments on both convex and non-convex problems and using various compression techniques.

Federated Optimization Algorithms with Random Reshuffling and Gradient Compression

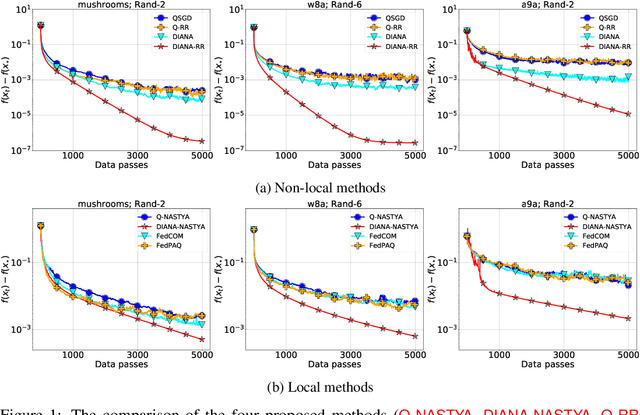
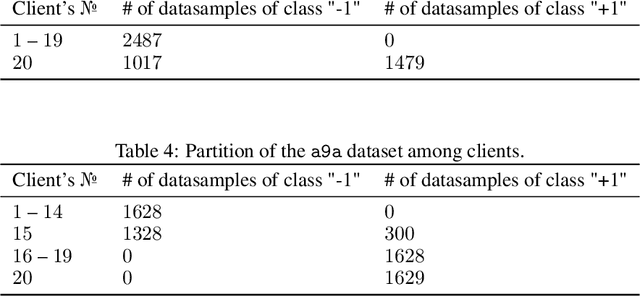
Gradient compression is a popular technique for improving communication complexity of stochastic first-order methods in distributed training of machine learning models. However, the existing works consider only with-replacement sampling of stochastic gradients. In contrast, it is well-known in practice and recently confirmed in theory that stochastic methods based on without-replacement sampling, e.g., Random Reshuffling (RR) method, perform better than ones that sample the gradients with-replacement. In this work, we close this gap in the literature and provide the first analysis of methods with gradient compression and without-replacement sampling. We first develop a distributed variant of random reshuffling with gradient compression (Q-RR), and show how to reduce the variance coming from gradient quantization through the use of control iterates. Next, to have a better fit to Federated Learning applications, we incorporate local computation and propose a variant of Q-RR called Q-NASTYA. Q-NASTYA uses local gradient steps and different local and global stepsizes. Next, we show how to reduce compression variance in this setting as well. Finally, we prove the convergence results for the proposed methods and outline several settings in which they improve upon existing algorithms.

Sharper Rates and Flexible Framework for Nonconvex SGD with Client and Data Sampling

We revisit the classical problem of finding an approximately stationary point of the average of $n$ smooth and possibly nonconvex functions. The optimal complexity of stochastic first-order methods in terms of the number of gradient evaluations of individual functions is $\mathcal{O}\left(n + n^{1/2}\varepsilon^{-1}\right)$, attained by the optimal SGD methods $\small\sf\color{green}{SPIDER}$(arXiv:1807.01695) and $\small\sf\color{green}{PAGE}$(arXiv:2008.10898), for example, where $\varepsilon$ is the error tolerance. However, i) the big-$\mathcal{O}$ notation hides crucial dependencies on the smoothness constants associated with the functions, and ii) the rates and theory in these methods assume simplistic sampling mechanisms that do not offer any flexibility. In this work we remedy the situation. First, we generalize the $\small\sf\color{green}{PAGE}$ algorithm so that it can provably work with virtually any (unbiased) sampling mechanism. This is particularly useful in federated learning, as it allows us to construct and better understand the impact of various combinations of client and data sampling strategies. Second, our analysis is sharper as we make explicit use of certain novel inequalities that capture the intricate interplay between the smoothness constants and the sampling procedure. Indeed, our analysis is better even for the simple sampling procedure analyzed in the $\small\sf\color{green}{PAGE}$ paper. However, this already improved bound can be further sharpened by a different sampling scheme which we propose. In summary, we provide the most general and most accurate analysis of optimal SGD in the smooth nonconvex regime. Finally, our theoretical findings are supposed with carefully designed experiments.