Cache Me If You Must: Adaptive Key-Value Quantization for Large Language Models

Efficient real-world deployments of large language models (LLMs) rely on Key-Value (KV) caching for processing and generating long outputs, reducing the need for repetitive computation. For large contexts, Key-Value caches can take up tens of gigabytes of device memory, as they store vector representations for each token and layer. Recent work has shown that the cached vectors can be compressed through quantization, pruning or merging, but these techniques often compromise quality towards higher compression rates. In this work, we aim to improve Key & Value compression by exploiting two observations: 1) the inherent dependencies between keys and values across different layers, and 2) high-compression mechanisms for internal network states. We propose AQUA-KV, an adaptive quantization for Key-Value caches that relies on compact adapters to exploit existing dependencies between Keys and Values, and aims to "optimally" compress the information that cannot be predicted. AQUA-KV significantly improves compression rates, while maintaining high accuracy on state-of-the-art LLM families. On Llama 3.2 LLMs, we achieve near-lossless inference at 2-2.5 bits per value with under $1\%$ relative error in perplexity and LongBench scores. AQUA-KV is one-shot, simple, and efficient: it can be calibrated on a single GPU within 1-6 hours, even for 70B models.

PV-Tuning: Beyond Straight-Through Estimation for Extreme LLM Compression

There has been significant interest in "extreme" compression of large language models (LLMs), i.e., to 1-2 bits per parameter, which allows such models to be executed efficiently on resource-constrained devices. Existing work focused on improved one-shot quantization techniques and weight representations; yet, purely post-training approaches are reaching diminishing returns in terms of the accuracy-vs-bit-width trade-off. State-of-the-art quantization methods such as QuIP# and AQLM include fine-tuning (part of) the compressed parameters over a limited amount of calibration data; however, such fine-tuning techniques over compressed weights often make exclusive use of straight-through estimators (STE), whose performance is not well-understood in this setting. In this work, we question the use of STE for extreme LLM compression, showing that it can be sub-optimal, and perform a systematic study of quantization-aware fine-tuning strategies for LLMs. We propose PV-Tuning - a representation-agnostic framework that generalizes and improves upon existing fine-tuning strategies, and provides convergence guarantees in restricted cases. On the practical side, when used for 1-2 bit vector quantization, PV-Tuning outperforms prior techniques for highly-performant models such as Llama and Mistral. Using PV-Tuning, we achieve the first Pareto-optimal quantization for Llama 2 family models at 2 bits per parameter.

Fast Inference of Mixture-of-Experts Language Models with Offloading

With the widespread adoption of Large Language Models (LLMs), many deep learning practitioners are looking for strategies of running these models more efficiently. One such strategy is to use sparse Mixture-of-Experts (MoE) - a type of model architectures where only a fraction of model layers are active for any given input. This property allows MoE-based language models to generate tokens faster than their dense counterparts, but it also increases model size due to having multiple experts. Unfortunately, this makes state-of-the-art MoE language models difficult to run without high-end GPUs. In this work, we study the problem of running large MoE language models on consumer hardware with limited accelerator memory. We build upon parameter offloading algorithms and propose a novel strategy that accelerates offloading by taking advantage of innate properties of MoE LLMs. Using this strategy, we build can run Mixtral-8x7B with mixed quantization on desktop hardware and free-tier Google Colab instances.

Distributed Deep Learning in Open Collaborations

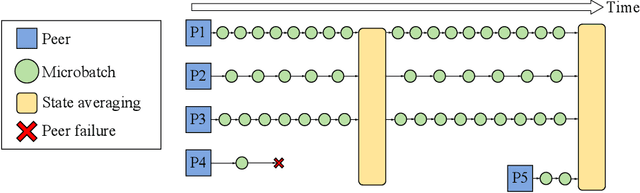
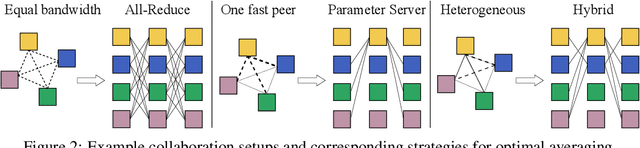
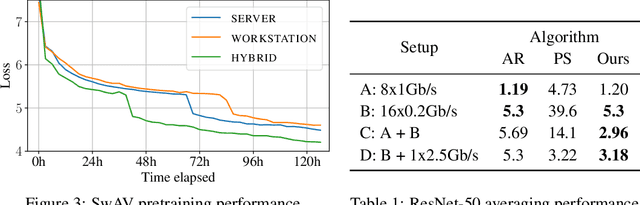
Modern deep learning applications require increasingly more compute to train state-of-the-art models. To address this demand, large corporations and institutions use dedicated High-Performance Computing clusters, whose construction and maintenance are both environmentally costly and well beyond the budget of most organizations. As a result, some research directions become the exclusive domain of a few large industrial and even fewer academic actors. To alleviate this disparity, smaller groups may pool their computational resources and run collaborative experiments that benefit all participants. This paradigm, known as grid- or volunteer computing, has seen successful applications in numerous scientific areas. However, using this approach for machine learning is difficult due to high latency, asymmetric bandwidth, and several challenges unique to volunteer computing. In this work, we carefully analyze these constraints and propose a novel algorithmic framework designed specifically for collaborative training. We demonstrate the effectiveness of our approach for SwAV and ALBERT pretraining in realistic conditions and achieve performance comparable to traditional setups at a fraction of the cost. Finally, we provide a detailed report of successful collaborative language model pretraining with 40 participants.

Beyond Vector Spaces: Compact Data Representation as Differentiable Weighted Graphs

Learning useful representations is a key ingredient to the success of modern machine learning. Currently, representation learning mostly relies on embedding data into Euclidean space. However, recent work has shown that data in some domains is better modeled by non-euclidean metric spaces, and inappropriate geometry can result in inferior performance. In this paper, we aim to eliminate the inductive bias imposed by the embedding space geometry. Namely, we propose to map data into more general non-vector metric spaces: a weighted graph with a shortest path distance. By design, such graphs can model arbitrary geometry with a proper configuration of edges and weights. Our main contribution is PRODIGE: a method that learns a weighted graph representation of data end-to-end by gradient descent. Greater generality and fewer model assumptions make PRODIGE more powerful than existing embedding-based approaches. We confirm the superiority of our method via extensive experiments on a wide range of tasks, including classification, compression, and collaborative filtering.