Error Feedback Reloaded: From Quadratic to Arithmetic Mean of Smoothness Constants

Error Feedback (EF) is a highly popular and immensely effective mechanism for fixing convergence issues which arise in distributed training methods (such as distributed GD or SGD) when these are enhanced with greedy communication compression techniques such as TopK. While EF was proposed almost a decade ago (Seide et al., 2014), and despite concentrated effort by the community to advance the theoretical understanding of this mechanism, there is still a lot to explore. In this work we study a modern form of error feedback called EF21 (Richtarik et al., 2021) which offers the currently best-known theoretical guarantees, under the weakest assumptions, and also works well in practice. In particular, while the theoretical communication complexity of EF21 depends on the quadratic mean of certain smoothness parameters, we improve this dependence to their arithmetic mean, which is always smaller, and can be substantially smaller, especially in heterogeneous data regimes. We take the reader on a journey of our discovery process. Starting with the idea of applying EF21 to an equivalent reformulation of the underlying problem which (unfortunately) requires (often impractical) machine cloning, we continue to the discovery of a new weighted version of EF21 which can (fortunately) be executed without any cloning, and finally circle back to an improved analysis of the original EF21 method. While this development applies to the simplest form of EF21, our approach naturally extends to more elaborate variants involving stochastic gradients and partial participation. Further, our technique improves the best-known theory of EF21 in the rare features regime (Richtarik et al., 2023). Finally, we validate our theoretical findings with suitable experiments.

Understanding Progressive Training Through the Framework of Randomized Coordinate Descent

We propose a Randomized Progressive Training algorithm (RPT) -- a stochastic proxy for the well-known Progressive Training method (PT) (Karras et al., 2017). Originally designed to train GANs (Goodfellow et al., 2014), PT was proposed as a heuristic, with no convergence analysis even for the simplest objective functions. On the contrary, to the best of our knowledge, RPT is the first PT-type algorithm with rigorous and sound theoretical guarantees for general smooth objective functions. We cast our method into the established framework of Randomized Coordinate Descent (RCD) (Nesterov, 2012; Richt\'arik & Tak\'a\v{c}, 2014), for which (as a by-product of our investigations) we also propose a novel, simple and general convergence analysis encapsulating strongly-convex, convex and nonconvex objectives. We then use this framework to establish a convergence theory for RPT. Finally, we validate the effectiveness of our method through extensive computational experiments.

Error Feedback Shines when Features are Rare

We provide the first proof that gradient descent $\left({\color{green}\sf GD}\right)$ with greedy sparsification $\left({\color{green}\sf TopK}\right)$ and error feedback $\left({\color{green}\sf EF}\right)$ can obtain better communication complexity than vanilla ${\color{green}\sf GD}$ when solving the distributed optimization problem $\min_{x\in \mathbb{R}^d} {f(x)=\frac{1}{n}\sum_{i=1}^n f_i(x)}$, where $n$ = # of clients, $d$ = # of features, and $f_1,\dots,f_n$ are smooth nonconvex functions. Despite intensive research since 2014 when ${\color{green}\sf EF}$ was first proposed by Seide et al., this problem remained open until now. We show that ${\color{green}\sf EF}$ shines in the regime when features are rare, i.e., when each feature is present in the data owned by a small number of clients only. To illustrate our main result, we show that in order to find a random vector $\hat{x}$ such that $\lVert {\nabla f(\hat{x})} \rVert^2 \leq \varepsilon$ in expectation, ${\color{green}\sf GD}$ with the ${\color{green}\sf Top1}$ sparsifier and ${\color{green}\sf EF}$ requires ${\cal O} \left(\left( L+{\color{blue}r} \sqrt{ \frac{{\color{red}c}}{n} \min \left( \frac{{\color{red}c}}{n} \max_i L_i^2, \frac{1}{n}\sum_{i=1}^n L_i^2 \right) }\right) \frac{1}{\varepsilon} \right)$ bits to be communicated by each worker to the server only, where $L$ is the smoothness constant of $f$, $L_i$ is the smoothness constant of $f_i$, ${\color{red}c}$ is the maximal number of clients owning any feature ($1\leq {\color{red}c} \leq n$), and ${\color{blue}r}$ is the maximal number of features owned by any client ($1\leq {\color{blue}r} \leq d$). Clearly, the communication complexity improves as ${\color{red}c}$ decreases (i.e., as features become more rare), and can be much better than the ${\cal O}({\color{blue}r} L \frac{1}{\varepsilon})$ communication complexity of ${\color{green}\sf GD}$ in the same regime.

Adaptive Compression for Communication-Efficient Distributed Training

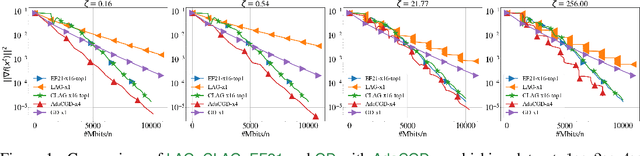
We propose Adaptive Compressed Gradient Descent (AdaCGD) - a novel optimization algorithm for communication-efficient training of supervised machine learning models with adaptive compression level. Our approach is inspired by the recently proposed three point compressor (3PC) framework of Richtarik et al. (2022), which includes error feedback (EF21), lazily aggregated gradient (LAG), and their combination as special cases, and offers the current state-of-the-art rates for these methods under weak assumptions. While the above mechanisms offer a fixed compression level, or adapt between two extremes only, our proposal is to perform a much finer adaptation. In particular, we allow the user to choose any number of arbitrarily chosen contractive compression mechanisms, such as Top-K sparsification with a user-defined selection of sparsification levels K, or quantization with a user-defined selection of quantization levels, or their combination. AdaCGD chooses the appropriate compressor and compression level adaptively during the optimization process. Besides i) proposing a theoretically-grounded multi-adaptive communication compression mechanism, we further ii) extend the 3PC framework to bidirectional compression, i.e., we allow the server to compress as well, and iii) provide sharp convergence bounds in the strongly convex, convex and nonconvex settings. The convex regime results are new even for several key special cases of our general mechanism, including 3PC and EF21. In all regimes, our rates are superior compared to all existing adaptive compression methods.

3PC: Three Point Compressors for Communication-Efficient Distributed Training and a Better Theory for Lazy Aggregation

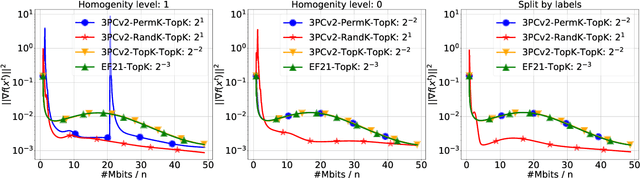
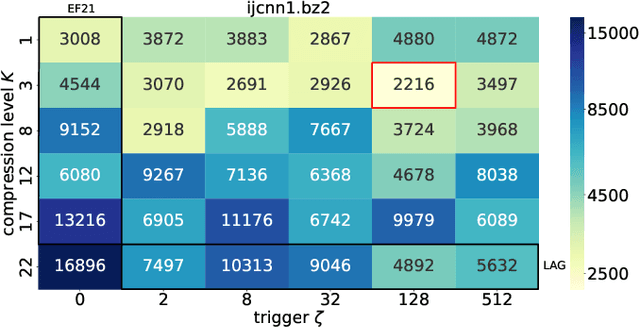
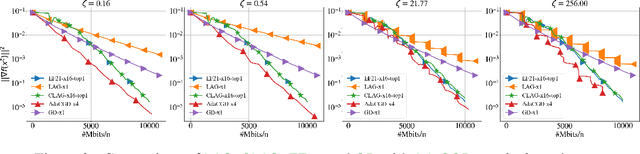
We propose and study a new class of gradient communication mechanisms for communication-efficient training -- three point compressors (3PC) -- as well as efficient distributed nonconvex optimization algorithms that can take advantage of them. Unlike most established approaches, which rely on a static compressor choice (e.g., Top-$K$), our class allows the compressors to {\em evolve} throughout the training process, with the aim of improving the theoretical communication complexity and practical efficiency of the underlying methods. We show that our general approach can recover the recently proposed state-of-the-art error feedback mechanism EF21 (Richt\'arik et al., 2021) and its theoretical properties as a special case, but also leads to a number of new efficient methods. Notably, our approach allows us to improve upon the state of the art in the algorithmic and theoretical foundations of the {\em lazy aggregation} literature (Chen et al., 2018). As a by-product that may be of independent interest, we provide a new and fundamental link between the lazy aggregation and error feedback literature. A special feature of our work is that we do not require the compressors to be unbiased.

FLIX: A Simple and Communication-Efficient Alternative to Local Methods in Federated Learning

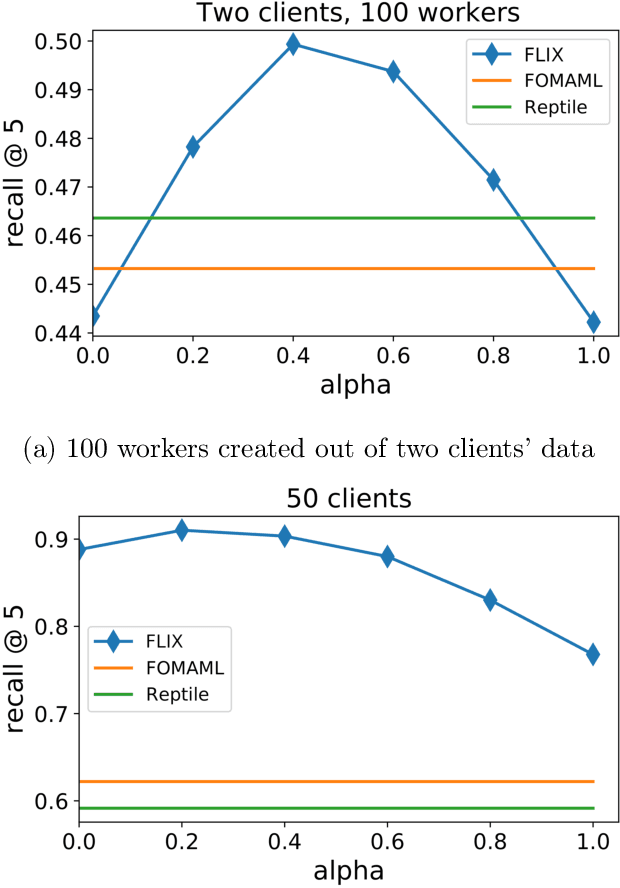
Federated Learning (FL) is an increasingly popular machine learning paradigm in which multiple nodes try to collaboratively learn under privacy, communication and multiple heterogeneity constraints. A persistent problem in federated learning is that it is not clear what the optimization objective should be: the standard average risk minimization of supervised learning is inadequate in handling several major constraints specific to federated learning, such as communication adaptivity and personalization control. We identify several key desiderata in frameworks for federated learning and introduce a new framework, FLIX, that takes into account the unique challenges brought by federated learning. FLIX has a standard finite-sum form, which enables practitioners to tap into the immense wealth of existing (potentially non-local) methods for distributed optimization. Through a smart initialization that does not require any communication, FLIX does not require the use of local steps but is still provably capable of performing dissimilarity regularization on par with local methods. We give several algorithms for solving the FLIX formulation efficiently under communication constraints. Finally, we corroborate our theoretical results with extensive experimentation.

Lower Bounds and Optimal Algorithms for Smooth and Strongly Convex Decentralized Optimization Over Time-Varying Networks

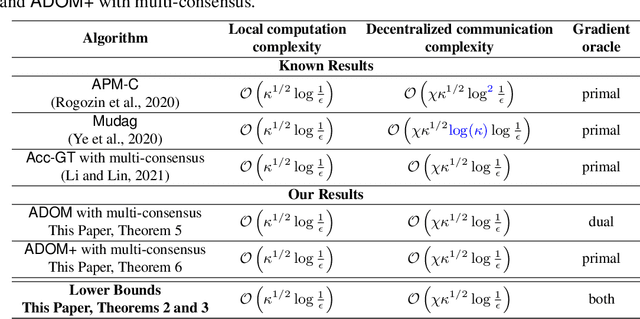
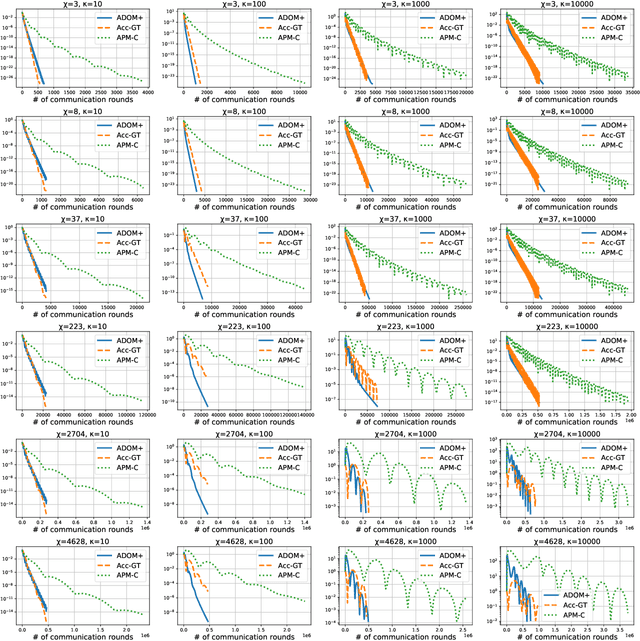
We consider the task of minimizing the sum of smooth and strongly convex functions stored in a decentralized manner across the nodes of a communication network whose links are allowed to change in time. We solve two fundamental problems for this task. First, we establish the first lower bounds on the number of decentralized communication rounds and the number of local computations required to find an $\epsilon$-accurate solution. Second, we design two optimal algorithms that attain these lower bounds: (i) a variant of the recently proposed algorithm ADOM (Kovalev et al., 2021) enhanced via a multi-consensus subroutine, which is optimal in the case when access to the dual gradients is assumed, and (ii) a novel algorithm, called ADOM+, which is optimal in the case when access to the primal gradients is assumed. We corroborate the theoretical efficiency of these algorithms by performing an experimental comparison with existing state-of-the-art methods.

From Local SGD to Local Fixed Point Methods for Federated Learning

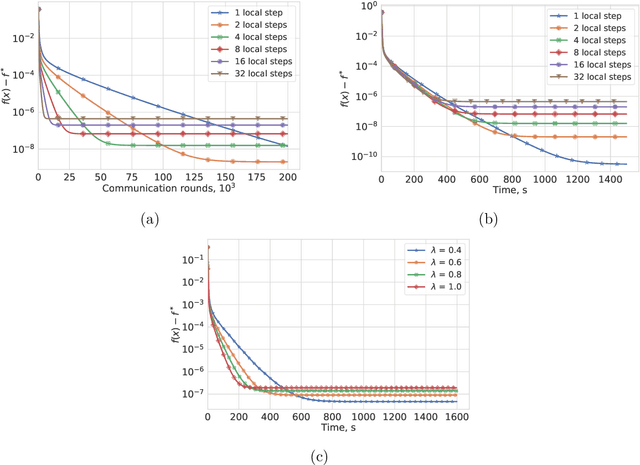
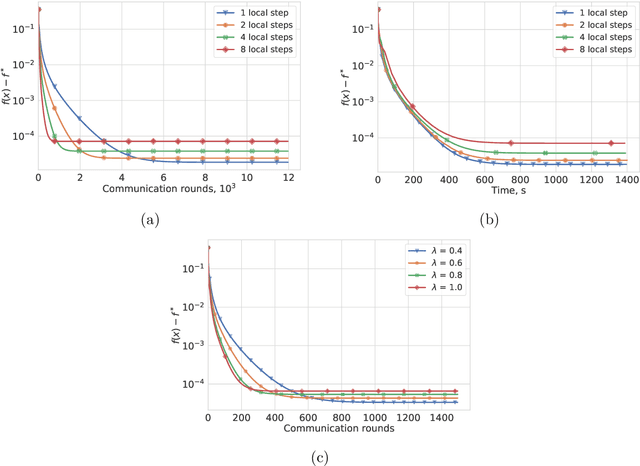
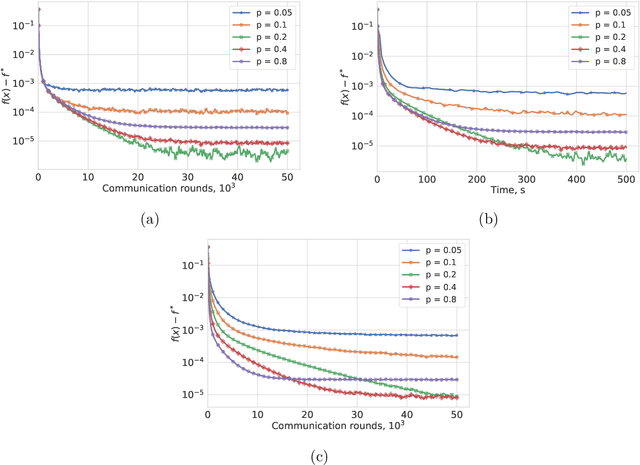
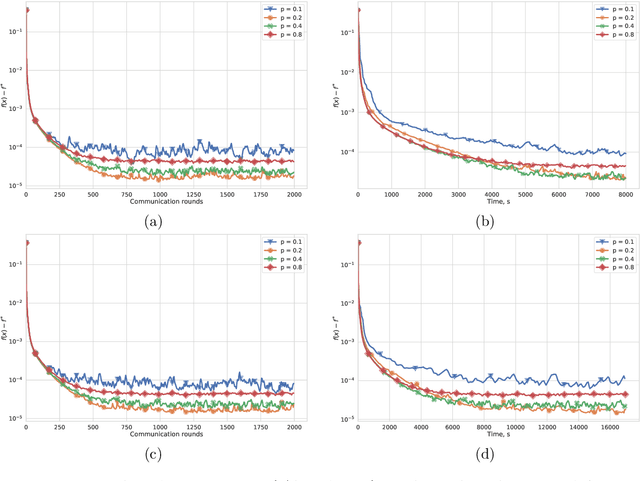
Most algorithms for solving optimization problems or finding saddle points of convex-concave functions are fixed point algorithms. In this work we consider the generic problem of finding a fixed point of an average of operators, or an approximation thereof, in a distributed setting. Our work is motivated by the needs of federated learning. In this context, each local operator models the computations done locally on a mobile device. We investigate two strategies to achieve such a consensus: one based on a fixed number of local steps, and the other based on randomized computations. In both cases, the goal is to limit communication of the locally-computed variables, which is often the bottleneck in distributed frameworks. We perform convergence analysis of both methods and conduct a number of experiments highlighting the benefits of our approach.