Lower Bounds and Optimal Algorithms for Smooth and Strongly Convex Decentralized Optimization Over Time-Varying Networks
Paper and Code
Jun 08, 2021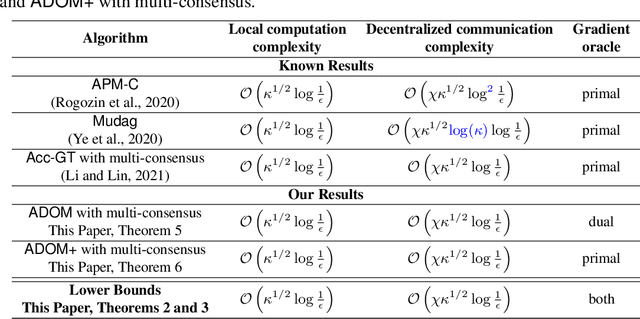

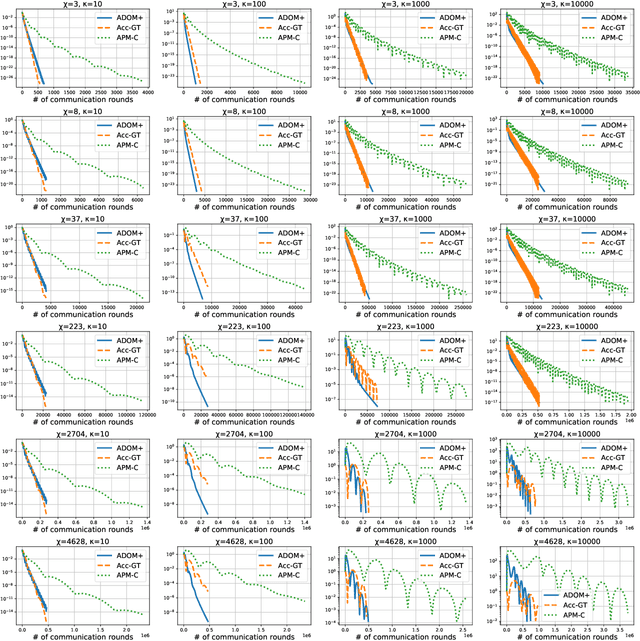
We consider the task of minimizing the sum of smooth and strongly convex functions stored in a decentralized manner across the nodes of a communication network whose links are allowed to change in time. We solve two fundamental problems for this task. First, we establish the first lower bounds on the number of decentralized communication rounds and the number of local computations required to find an $\epsilon$-accurate solution. Second, we design two optimal algorithms that attain these lower bounds: (i) a variant of the recently proposed algorithm ADOM (Kovalev et al., 2021) enhanced via a multi-consensus subroutine, which is optimal in the case when access to the dual gradients is assumed, and (ii) a novel algorithm, called ADOM+, which is optimal in the case when access to the primal gradients is assumed. We corroborate the theoretical efficiency of these algorithms by performing an experimental comparison with existing state-of-the-art methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge