Convergence of Clipped-SGD for Convex $(L_0,L_1)$-Smooth Optimization with Heavy-Tailed Noise

Gradient clipping is a widely used technique in Machine Learning and Deep Learning (DL), known for its effectiveness in mitigating the impact of heavy-tailed noise, which frequently arises in the training of large language models. Additionally, first-order methods with clipping, such as Clip-SGD, exhibit stronger convergence guarantees than SGD under the $(L_0,L_1)$-smoothness assumption, a property observed in many DL tasks. However, the high-probability convergence of Clip-SGD under both assumptions -- heavy-tailed noise and $(L_0,L_1)$-smoothness -- has not been fully addressed in the literature. In this paper, we bridge this critical gap by establishing the first high-probability convergence bounds for Clip-SGD applied to convex $(L_0,L_1)$-smooth optimization with heavy-tailed noise. Our analysis extends prior results by recovering known bounds for the deterministic case and the stochastic setting with $L_1 = 0$ as special cases. Notably, our rates avoid exponentially large factors and do not rely on restrictive sub-Gaussian noise assumptions, significantly broadening the applicability of gradient clipping.

Variance Reduction Methods Do Not Need to Compute Full Gradients: Improved Efficiency through Shuffling

In today's world, machine learning is hard to imagine without large training datasets and models. This has led to the use of stochastic methods for training, such as stochastic gradient descent (SGD). SGD provides weak theoretical guarantees of convergence, but there are modifications, such as Stochastic Variance Reduced Gradient (SVRG) and StochAstic Recursive grAdient algoritHm (SARAH), that can reduce the variance. These methods require the computation of the full gradient occasionally, which can be time consuming. In this paper, we explore variants of variance reduction algorithms that eliminate the need for full gradient computations. To make our approach memory-efficient and avoid full gradient computations, we use two key techniques: the shuffling heuristic and idea of SAG/SAGA methods. As a result, we improve existing estimates for variance reduction algorithms without the full gradient computations. Additionally, for the non-convex objective function, our estimate matches that of classic shuffling methods, while for the strongly convex one, it is an improvement. We conduct comprehensive theoretical analysis and provide extensive experimental results to validate the efficiency and practicality of our methods for large-scale machine learning problems.

Gradient Clipping Improves AdaGrad when the Noise Is Heavy-Tailed

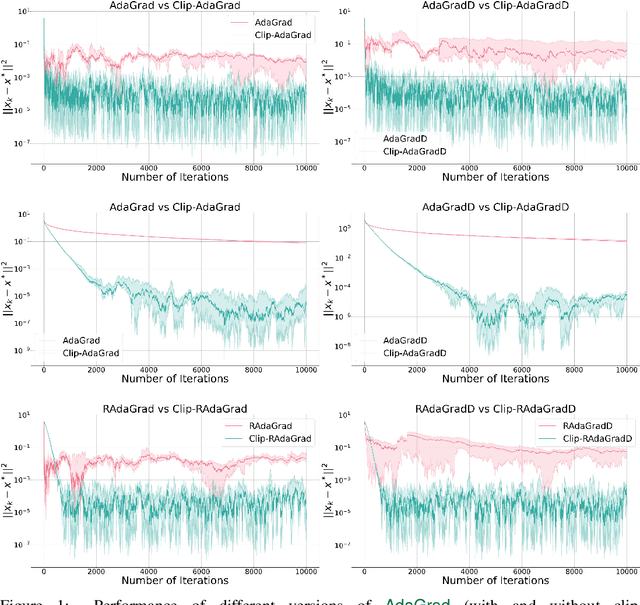
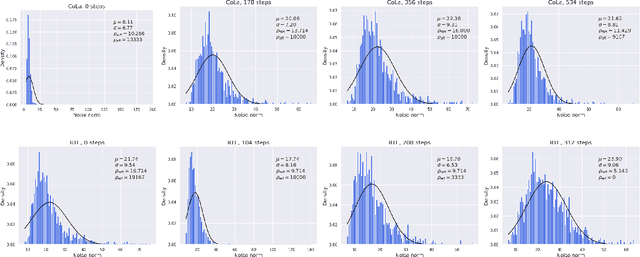
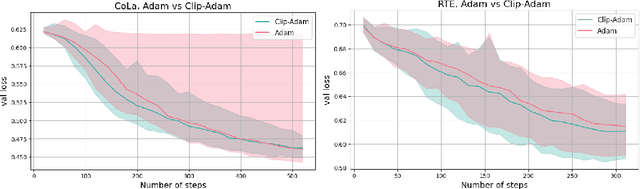
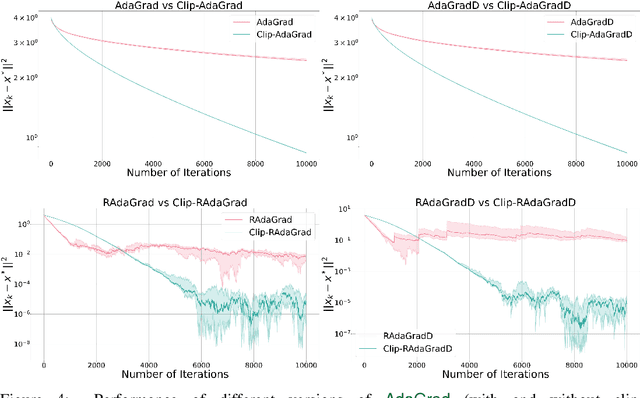
Methods with adaptive stepsizes, such as AdaGrad and Adam, are essential for training modern Deep Learning models, especially Large Language Models. Typically, the noise in the stochastic gradients is heavy-tailed for the later ones. Gradient clipping provably helps to achieve good high-probability convergence for such noises. However, despite the similarity between AdaGrad/Adam and Clip-SGD, the high-probability convergence of AdaGrad/Adam has not been studied in this case. In this work, we prove that AdaGrad (and its delayed version) can have provably bad high-probability convergence if the noise is heavy-tailed. To fix this issue, we propose a new version of AdaGrad called Clip-RAdaGradD (Clipped Reweighted AdaGrad with Delay) and prove its high-probability convergence bounds with polylogarithmic dependence on the confidence level for smooth convex/non-convex stochastic optimization with heavy-tailed noise. Our empirical evaluations, including NLP model fine-tuning, highlight the superiority of clipped versions of AdaGrad/Adam in handling the heavy-tailed noise.

Local Methods with Adaptivity via Scaling

The rapid development of machine learning and deep learning has introduced increasingly complex optimization challenges that must be addressed. Indeed, training modern, advanced models has become difficult to implement without leveraging multiple computing nodes in a distributed environment. Distributed optimization is also fundamental to emerging fields such as federated learning. Specifically, there is a need to organize the training process to minimize the time lost due to communication. A widely used and extensively researched technique to mitigate the communication bottleneck involves performing local training before communication. This approach is the focus of our paper. Concurrently, adaptive methods that incorporate scaling, notably led by Adam, have gained significant popularity in recent years. Therefore, this paper aims to merge the local training technique with the adaptive approach to develop efficient distributed learning methods. We consider the classical Local SGD method and enhance it with a scaling feature. A crucial aspect is that the scaling is described generically, allowing us to analyze various approaches, including Adam, RMSProp, and OASIS, in a unified manner. In addition to theoretical analysis, we validate the performance of our methods in practice by training a neural network.