Synthetic Persona Pretraining: Alignment from Token Zero

As language-model-based AI is increasingly deployed in autonomous settings, aligning its goals and values with those of humans becomes critical. Today, alignment, and the assistant identity itself, are typically introduced only after pretraining, once behavioral priors are already established. This can make values a thin overlay, rather than deeply rooted, and facilitate subsequent misalignment. Pursuing a different paradigm, we introduce Synthetic Persona Pretraining (SPP), which installs the desired assistant persona from token zero in pretraining. First, we annotate pretraining documents with value-aligned first-person reflections derived from a normative value constitution. Second, we pretrain via the standard cross-entropy loss on standard pretraining documents as well as their reflections, which installs the desired persona among a multitude of other personas. Finally, we post-train on user-assistant dialogue data, which binds this desired persona to the assistant identity, a process we call persona binding. By pretraining models up to 3B parameters on 500B tokens, we show that SPP improves constitution following and jailbreak robustness, and reduces the misalignment rate in out-of-distribution moral dilemmas, while preserving capabilities. Early intervention matters: compared with alignment from token zero, introducing SPP only at the end of pretraining yields weaker constitution adherence, does not shift value priorities, and leads to less aligned choices in dilemmas. This advantage depends on persona binding and, importantly, increases with pretraining budget. Overall, our results show that shaping values early is critical for alignment and establish pretraining-time persona interventions as an effective approach to do so.

Flow Map Learning via Nongradient Vector Flow

Diffusion and flow-based models benefit from simple regression losses, but inference incurs significant overhead because sampling requires integration. Consistency models address this by directly learning the flow maps along the ODE trajectory, opening a design space between one-step and many-step approaches. However, existing methods face computational challenges such as requiring model inverses or backpropagation through iterated model calls, and do not always prove that the desired ODE flow map is a solution to the loss. We introduce SGFlow, an approach for learning flow maps that bypasses explicit invertibility constraints and expensive differentiation through model iteration. SGFlow trains a model to compute both the ODE solutions and the implied velocity from scratch by following non-conservative dynamics with a stationary point at the desired flow map. On the CIFAR image benchmark, no single method attains the best FID at every step count: SGFlow attains the best FID at 10 sampling steps and remains competitive with flow matching, Meanflow, and Lagrangian map matching at other step counts, while being the only one with a proven stationary-point guarantee for its stopgrad-based dynamics.

Tandem Reinforcement Learning with Verifiable Rewards

Reinforcement learning with verifiable rewards (RLVR) has significantly improved the reasoning capability of large language models, reaching expert or even superhuman performance in domains such as competition math. However, whether weaker agents and humans can actually harness this capability is far less certain, with RLVR documented to drift reasoning toward idiosyncratic patterns such as poor readability and language mixing. Tandem training is a recently introduced paradigm that targets this compatibility problem: a trained, stronger senior co-generates each rollout with a frozen, weaker junior, and the two are rewarded as a team, so the senior is pushed to reason in ways the junior can follow. Yet this paradigm has so far been demonstrated only in proof-of-concept settings, leaving open whether it scales to the long chains of thought of the modern RLVR pipeline. In this work, we propose Tandem Reinforcement Learning (TRL), which carries the tandem training paradigm into RLVR. In TRL, the senior and a frozen junior alternate stochastically to co-generate the reasoning, the resulting generation is rewarded, and the standard GRPO loss is applied to the senior. Training Qwen3-4B-Instruct on competition math, we find that TRL matches vanilla GRPO on solo reasoning capability while three properties emerge together from the same rollout structure: stronger handoff robustness with the junior, reduced distributional drift from the junior, and a chain-of-thought more legible to the junior. Our results demonstrate a promising route for RLVR with practical payoffs in multi-model communication and human compatibility.

Estimating Tail Risks in Language Model Output Distributions

Language models are increasingly capable and are being rapidly deployed on a population-level scale. As a result, the safety of these models is increasingly high-stakes. Fortunately, advances in alignment have significantly reduced the likelihood of harmful model outputs. However, when models are queried billions of times in a day, even rare worst-case behaviors will occur. Current safety evaluations focus on capturing the distribution of inputs that yield harmful outputs. These evaluations disregard the probabilistic nature of models and their tail output behavior. To measure this tail risk, we propose a method to efficiently estimate the probability of harmful outputs for any input query. Instead of naive brute-force sampling from the target model, where harmful outputs could be rare, we operationalize importance sampling by creating unsafe versions of the target model. These unsafe versions enable sample-efficient estimation by making harmful outputs more probable. On benchmarks measuring misuse and misalignment, these estimates match brute-force Monte Carlo estimates using 10-20x fewer samples. For example, we can estimate probability of harmful outputs on the order of 10^-4 with just 500 samples. Additionally, we find that these harmfulness estimates can reveal the sensitivity of models to perturbations in model input and predict deployment risks. Our work demonstrates that accurate rare-event estimation is both critical and feasible for safety evaluations. Code is available at https://github.com/rangell/LMTailRisk

Reject, Resample, Repeat: Understanding Parallel Reasoning in Language Model Inference

Inference-time methods that aggregate and prune multiple samples have emerged as a powerful paradigm for steering large language models, yet we lack any principled understanding of their accuracy-cost tradeoffs. In this paper, we introduce a route to rigorously study such approaches using the lens of *particle filtering* algorithms such as Sequential Monte Carlo (SMC). Given a base language model and a *process reward model* estimating expected terminal rewards, we ask: *how accurately can we sample from a target distribution given some number of process reward evaluations?* Theoretically, we identify (1) simple criteria enabling non-asymptotic guarantees for SMC; (2) algorithmic improvements to SMC; and (3) a fundamental limit faced by all particle filtering methods. Empirically, we demonstrate that our theoretical criteria effectively govern the *sampling error* of SMC, though not necessarily its final *accuracy*, suggesting that theoretical perspectives beyond sampling may be necessary.

Apertus: Democratizing Open and Compliant LLMs for Global Language Environments

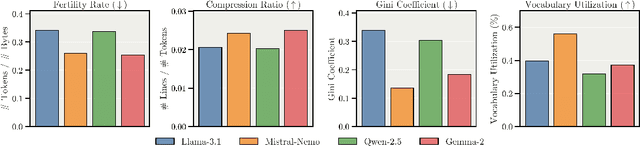
We present Apertus, a fully open suite of large language models (LLMs) designed to address two systemic shortcomings in today's open model ecosystem: data compliance and multilingual representation. Unlike many prior models that release weights without reproducible data pipelines or regard for content-owner rights, Apertus models are pretrained exclusively on openly available data, retroactively respecting robots.txt exclusions and filtering for non-permissive, toxic, and personally identifiable content. To mitigate risks of memorization, we adopt the Goldfish objective during pretraining, strongly suppressing verbatim recall of data while retaining downstream task performance. The Apertus models also expand multilingual coverage, training on 15T tokens from over 1800 languages, with ~40% of pretraining data allocated to non-English content. Released at 8B and 70B scales, Apertus approaches state-of-the-art results among fully open models on multilingual benchmarks, rivalling or surpassing open-weight counterparts. Beyond model weights, we release all scientific artifacts from our development cycle with a permissive license, including data preparation scripts, checkpoints, evaluation suites, and training code, enabling transparent audit and extension.

Safety Subspaces are Not Distinct: A Fine-Tuning Case Study

Large Language Models (LLMs) rely on safety alignment to produce socially acceptable responses. This is typically achieved through instruction tuning and reinforcement learning from human feedback. However, this alignment is known to be brittle: further fine-tuning, even on benign or lightly contaminated data, can degrade safety and reintroduce harmful behaviors. A growing body of work suggests that alignment may correspond to identifiable geometric directions in weight space, forming subspaces that could, in principle, be isolated or preserved to defend against misalignment. In this work, we conduct a comprehensive empirical study of this geometric perspective. We examine whether safety-relevant behavior is concentrated in specific subspaces, whether it can be separated from general-purpose learning, and whether harmfulness arises from distinguishable patterns in internal representations. Across both parameter and activation space, our findings are consistent: subspaces that amplify safe behaviors also amplify unsafe ones, and prompts with different safety implications activate overlapping representations. We find no evidence of a subspace that selectively governs safety. These results challenge the assumption that alignment is geometrically localized. Rather than residing in distinct directions, safety appears to emerge from entangled, high-impact components of the model's broader learning dynamics. This suggests that subspace-based defenses may face fundamental limitations and underscores the need for alternative strategies to preserve alignment under continued training. We corroborate these findings through multiple experiments on five open-source LLMs. Our code is publicly available at: https://github.com/CERT-Lab/safety-subspaces.

ABBA: Highly Expressive Hadamard Product Adaptation for Large Language Models

Large Language Models have demonstrated strong performance across a wide range of tasks, but adapting them efficiently to new domains remains a key challenge. Parameter-Efficient Fine-Tuning (PEFT) methods address this by introducing lightweight, trainable modules while keeping most pre-trained weights fixed. The prevailing approach, LoRA, models updates using a low-rank decomposition, but its expressivity is inherently constrained by the rank. Recent methods like HiRA aim to increase expressivity by incorporating a Hadamard product with the frozen weights, but still rely on the structure of the pre-trained model. We introduce ABBA, a new PEFT architecture that reparameterizes the update as a Hadamard product of two independently learnable low-rank matrices. In contrast to prior work, ABBA fully decouples the update from the pre-trained weights, enabling both components to be optimized freely. This leads to significantly higher expressivity under the same parameter budget. We formally analyze ABBA's expressive capacity and validate its advantages through matrix reconstruction experiments. Empirically, ABBA achieves state-of-the-art results on arithmetic and commonsense reasoning benchmarks, consistently outperforming existing PEFT methods by a significant margin across multiple models. Our code is publicly available at: https://github.com/CERT-Lab/abba.

Regularization-based Framework for Quantization-, Fault- and Variability-Aware Training

Efficient inference is critical for deploying deep learning models on edge AI devices. Low-bit quantization (e.g., 3- and 4-bit) with fixed-point arithmetic improves efficiency, while low-power memory technologies like analog nonvolatile memory enable further gains. However, these methods introduce non-ideal hardware behavior, including bit faults and device-to-device variability. We propose a regularization-based quantization-aware training (QAT) framework that supports fixed, learnable step-size, and learnable non-uniform quantization, achieving competitive results on CIFAR-10 and ImageNet. Our method also extends to Spiking Neural Networks (SNNs), demonstrating strong performance on 4-bit networks on CIFAR10-DVS and N-Caltech 101. Beyond quantization, our framework enables fault and variability-aware fine-tuning, mitigating stuck-at faults (fixed weight bits) and device resistance variability. Compared to prior fault-aware training, our approach significantly improves performance recovery under upto 20% bit-fault rate and 40% device-to-device variability. Our results establish a generalizable framework for quantization and robustness-aware training, enhancing efficiency and reliability in low-power, non-ideal hardware.

Fed-SB: A Silver Bullet for Extreme Communication Efficiency and Performance in (Private) Federated LoRA Fine-Tuning

Low-Rank Adaptation (LoRA) has become ubiquitous for efficiently fine-tuning foundation models. However, federated fine-tuning using LoRA is challenging due to suboptimal updates arising from traditional federated averaging of individual adapters. Existing solutions either incur prohibitively high communication cost that scales linearly with the number of clients or suffer from performance degradation due to limited expressivity. We introduce Federated Silver Bullet (Fed-SB), a novel approach for federated fine-tuning of LLMs using LoRA-SB, a recently proposed low-rank adaptation method. LoRA-SB optimally aligns the optimization trajectory with the ideal low-rank full fine-tuning projection by learning a small square matrix (R) between adapters B and A, keeping other components fixed. Direct averaging of R guarantees exact updates, substantially reducing communication cost, which remains independent of the number of clients, and enables scalability. Fed-SB achieves state-of-the-art performance across commonsense reasoning, arithmetic reasoning, and language inference tasks while reducing communication costs by up to 230x. In private settings, Fed-SB further improves performance by (1) reducing trainable parameters, thereby lowering the noise required for differential privacy and (2) avoiding noise amplification introduced by other methods. Overall, Fed-SB establishes a new Pareto frontier in the tradeoff between communication and performance, offering an efficient and scalable solution for both private and non-private federated fine-tuning. Our code is publicly available at https://github.com/CERT-Lab/fed-sb.