Improving Stochastic Cubic Newton with Momentum

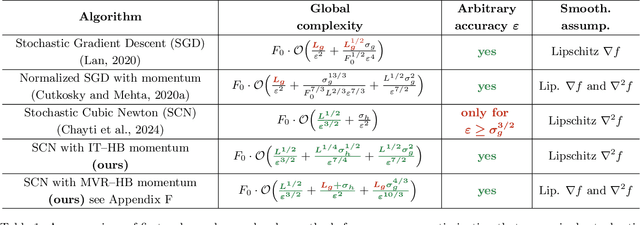
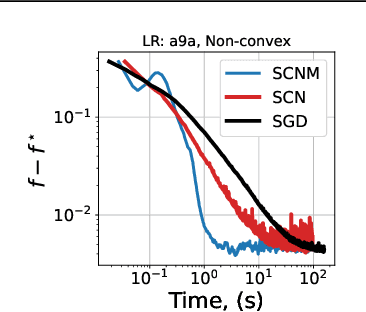
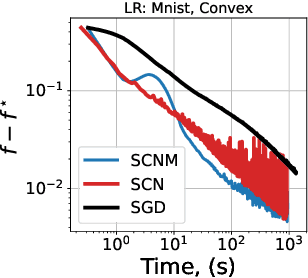
We study stochastic second-order methods for solving general non-convex optimization problems. We propose using a special version of momentum to stabilize the stochastic gradient and Hessian estimates in Newton's method. We show that momentum provably improves the variance of stochastic estimates and allows the method to converge for any noise level. Using the cubic regularization technique, we prove a global convergence rate for our method on general non-convex problems to a second-order stationary point, even when using only a single stochastic data sample per iteration. This starkly contrasts with all existing stochastic second-order methods for non-convex problems, which typically require large batches. Therefore, we are the first to demonstrate global convergence for batches of arbitrary size in the non-convex case for the Stochastic Cubic Newton. Additionally, we show improved speed on convex stochastic problems for our regularized Newton methods with momentum.

Cubic regularized subspace Newton for non-convex optimization

This paper addresses the optimization problem of minimizing non-convex continuous functions, which is relevant in the context of high-dimensional machine learning applications characterized by over-parametrization. We analyze a randomized coordinate second-order method named SSCN which can be interpreted as applying cubic regularization in random subspaces. This approach effectively reduces the computational complexity associated with utilizing second-order information, rendering it applicable in higher-dimensional scenarios. Theoretically, we establish convergence guarantees for non-convex functions, with interpolating rates for arbitrary subspace sizes and allowing inexact curvature estimation. When increasing subspace size, our complexity matches $\mathcal{O}(\epsilon^{-3/2})$ of the cubic regularization (CR) rate. Additionally, we propose an adaptive sampling scheme ensuring exact convergence rate of $\mathcal{O}(\epsilon^{-3/2}, \epsilon^{-3})$ to a second-order stationary point, even without sampling all coordinates. Experimental results demonstrate substantial speed-ups achieved by SSCN compared to conventional first-order methods.

First and zeroth-order implementations of the regularized Newton method with lazy approximated Hessians

In this work, we develop first-order (Hessian-free) and zero-order (derivative-free) implementations of the Cubically regularized Newton method for solving general non-convex optimization problems. For that, we employ finite difference approximations of the derivatives. We use a special adaptive search procedure in our algorithms, which simultaneously fits both the regularization constant and the parameters of the finite difference approximations. It makes our schemes free from the need to know the actual Lipschitz constants. Additionally, we equip our algorithms with the lazy Hessian update that reuse a previously computed Hessian approximation matrix for several iterations. Specifically, we prove the global complexity bound of $\mathcal{O}( n^{1/2} \epsilon^{-3/2})$ function and gradient evaluations for our new Hessian-free method, and a bound of $\mathcal{O}( n^{3/2} \epsilon^{-3/2} )$ function evaluations for the derivative-free method, where $n$ is the dimension of the problem and $\epsilon$ is the desired accuracy for the gradient norm. These complexity bounds significantly improve the previously known ones in terms of the joint dependence on $n$ and $\epsilon$, for the first-order and zeroth-order non-convex optimization.

Minimizing Quasi-Self-Concordant Functions by Gradient Regularization of Newton Method

We study the composite convex optimization problems with a Quasi-Self-Concordant smooth component. This problem class naturally interpolates between classic Self-Concordant functions and functions with Lipschitz continuous Hessian. Previously, the best complexity bounds for this problem class were associated with trust-region schemes and implementations of a ball-minimization oracle. In this paper, we show that for minimizing Quasi-Self-Concordant functions we can use instead the basic Newton Method with Gradient Regularization. For unconstrained minimization, it only involves a simple matrix inversion operation (solving a linear system) at each step. We prove a fast global linear rate for this algorithm, matching the complexity bound of the trust-region scheme, while our method remains especially simple to implement. Then, we introduce the Dual Newton Method, and based on it, develop the corresponding Accelerated Newton Scheme for this problem class, which further improves the complexity factor of the basic method. As a direct consequence of our results, we establish fast global linear rates of simple variants of the Newton Method applied to several practical problems, including Logistic Regression, Soft Maximum, and Matrix Scaling, without requiring additional assumptions on strong or uniform convexity for the target objective.

Shuffle SGD is Always Better than SGD: Improved Analysis of SGD with Arbitrary Data Orders

Stochastic Gradient Descent (SGD) algorithms are widely used in optimizing neural networks, with Random Reshuffling (RR) and Single Shuffle (SS) being popular choices for cycling through random or single permutations of the training data. However, the convergence properties of these algorithms in the non-convex case are not fully understood. Existing results suggest that, in realistic training scenarios where the number of epochs is smaller than the training set size, RR may perform worse than SGD. In this paper, we analyze a general SGD algorithm that allows for arbitrary data orderings and show improved convergence rates for non-convex functions. Specifically, our analysis reveals that SGD with random and single shuffling is always faster or at least as good as classical SGD with replacement, regardless of the number of iterations. Overall, our study highlights the benefits of using SGD with random/single shuffling and provides new insights into its convergence properties for non-convex optimization.

Linearization Algorithms for Fully Composite Optimization

In this paper, we study first-order algorithms for solving fully composite optimization problems over bounded sets. We treat the differentiable and non-differentiable parts of the objective separately, linearizing only the smooth components. This provides us with new generalizations of the classical and accelerated Frank-Wolfe methods, that are applicable to non-differentiable problems whenever we can access the structure of the objective. We prove global complexity bounds for our algorithms that are optimal in several settings.

Unified Convergence Theory of Stochastic and Variance-Reduced Cubic Newton Methods

We study the widely known Cubic-Newton method in the stochastic setting and propose a general framework to use variance reduction which we call the helper framework. In all previous work, these methods were proposed with very large batches (both in gradients and Hessians) and with various and often strong assumptions. In this work, we investigate the possibility of using such methods without large batches and use very simple assumptions that are sufficient for all our methods to work. In addition, we study these methods applied to gradient-dominated functions. In the general case, we show improved convergence (compared to first-order methods) to an approximate local minimum, and for gradient-dominated functions, we show convergence to approximate global minima.

Polynomial Preconditioning for Gradient Methods

We study first-order methods with preconditioning for solving structured nonlinear convex optimization problems. We propose a new family of preconditioners generated by symmetric polynomials. They provide first-order optimization methods with a provable improvement of the condition number, cutting the gaps between highest eigenvalues, without explicit knowledge of the actual spectrum. We give a stochastic interpretation of this preconditioning in terms of coordinate volume sampling and compare it with other classical approaches, including the Chebyshev polynomials. We show how to incorporate a polynomial preconditioning into the Gradient and Fast Gradient Methods and establish the corresponding global complexity bounds. Finally, we propose a simple adaptive search procedure that automatically chooses the best possible polynomial preconditioning for the Gradient Method, minimizing the objective along a low-dimensional Krylov subspace. Numerical experiments confirm the efficiency of our preconditioning strategies for solving various machine learning problems.

Second-order optimization with lazy Hessians

We analyze Newton's method with lazy Hessian updates for solving general possibly non-convex optimization problems. We propose to reuse a previously seen Hessian for several iterations while computing new gradients at each step of the method. This significantly reduces the overall arithmetical complexity of second-order optimization schemes. By using the cubic regularization technique, we establish fast global convergence of our method to a second-order stationary point, while the Hessian does not need to be updated each iteration. For convex problems, we justify global and local superlinear rates for lazy Newton steps with quadratic regularization, which is easier to compute. The optimal frequency for updating the Hessian is once every $d$ iterations, where $d$ is the dimension of the problem. This provably improves the total arithmetical complexity of second-order algorithms by a factor $\sqrt{d}$.

Super-Universal Regularized Newton Method

We analyze the performance of a variant of Newton method with quadratic regularization for solving composite convex minimization problems. At each step of our method, we choose regularization parameter proportional to a certain power of the gradient norm at the current point. We introduce a family of problem classes characterized by H\"older continuity of either the second or third derivative. Then we present the method with a simple adaptive search procedure allowing an automatic adjustment to the problem class with the best global complexity bounds, without knowing specific parameters of the problem. In particular, for the class of functions with Lipschitz continuous third derivative, we get the global $O(1/k^3)$ rate, which was previously attributed to third-order tensor methods. When the objective function is uniformly convex, we justify an automatic acceleration of our scheme, resulting in a faster global rate and local superlinear convergence. The switching between the different rates (sublinear, linear, and superlinear) is automatic. Again, for that, no a priori knowledge of parameters is needed.