Theoretical characterisation of the Gauss-Newton conditioning in Neural Networks

The Gauss-Newton (GN) matrix plays an important role in machine learning, most evident in its use as a preconditioning matrix for a wide family of popular adaptive methods to speed up optimization. Besides, it can also provide key insights into the optimization landscape of neural networks. In the context of deep neural networks, understanding the GN matrix involves studying the interaction between different weight matrices as well as the dependencies introduced by the data, thus rendering its analysis challenging. In this work, we take a first step towards theoretically characterizing the conditioning of the GN matrix in neural networks. We establish tight bounds on the condition number of the GN in deep linear networks of arbitrary depth and width, which we also extend to two-layer ReLU networks. We expand the analysis to further architectural components, such as residual connections and convolutional layers. Finally, we empirically validate the bounds and uncover valuable insights into the influence of the analyzed architectural components.

Cubic regularized subspace Newton for non-convex optimization

This paper addresses the optimization problem of minimizing non-convex continuous functions, which is relevant in the context of high-dimensional machine learning applications characterized by over-parametrization. We analyze a randomized coordinate second-order method named SSCN which can be interpreted as applying cubic regularization in random subspaces. This approach effectively reduces the computational complexity associated with utilizing second-order information, rendering it applicable in higher-dimensional scenarios. Theoretically, we establish convergence guarantees for non-convex functions, with interpolating rates for arbitrary subspace sizes and allowing inexact curvature estimation. When increasing subspace size, our complexity matches $\mathcal{O}(\epsilon^{-3/2})$ of the cubic regularization (CR) rate. Additionally, we propose an adaptive sampling scheme ensuring exact convergence rate of $\mathcal{O}(\epsilon^{-3/2}, \epsilon^{-3})$ to a second-order stationary point, even without sampling all coordinates. Experimental results demonstrate substantial speed-ups achieved by SSCN compared to conventional first-order methods.

A CT Image Denoising Method with Residual Encoder-Decoder Network

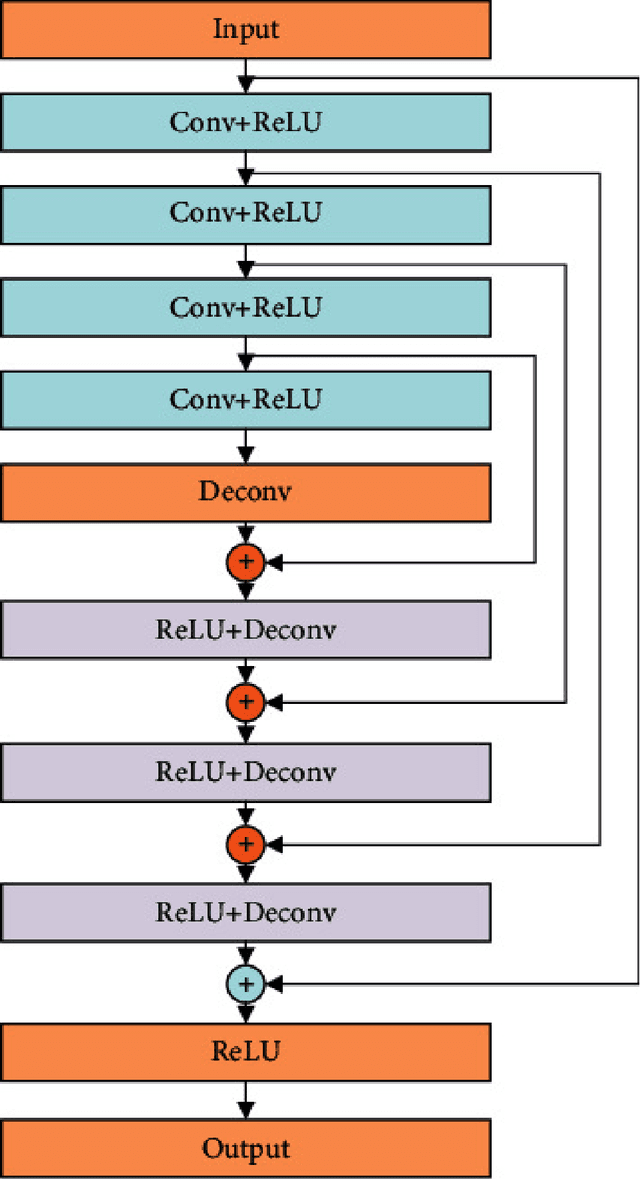
Utilizing a low-dose CT approach significantly reduces the radiation exposure for patients, yet it introduces challenges, such as increased noise and artifacts in the resultant images, which can hinder accurate medical diagnostics. Traditional methods for noise reduction struggle with preserving image textures due to the complexity of modeling statistical properties directly within the image domain. To address these limitations, this study introduces an enhanced noise-reduction technique centered around an advanced residual encoder-decoder network. By incorporating recursive processing into the foundational network, this method reduces computational complexity and enhances the effectiveness of noise reduction. Furthermore, the introduction of a root-mean-square error and perceptual loss functions aims to retain the integrity of the images' textural details. The enhanced technique also includes optimized tissue segmentation, improving artifact management post-improvement. Validation using the TCGA-COAD clinical dataset demonstrates superior performance in both noise reduction and image quality, as measured by post-denoising PSNR and SSIM, compared to the existing WGAN approach. This advancement in CT image processing offers a practical solution for clinical applications, achieving lower computational demands and faster processing times without compromising image quality.

The Limits of Perception: Analyzing Inconsistencies in Saliency Maps in XAI

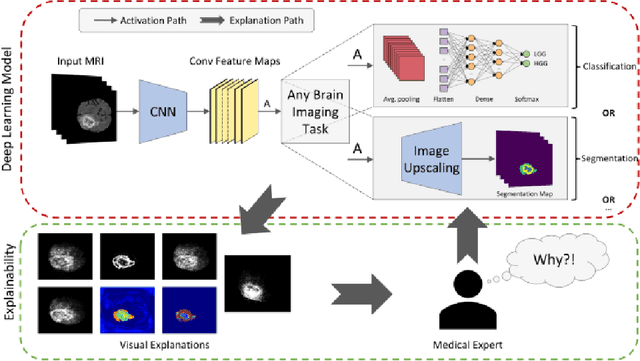
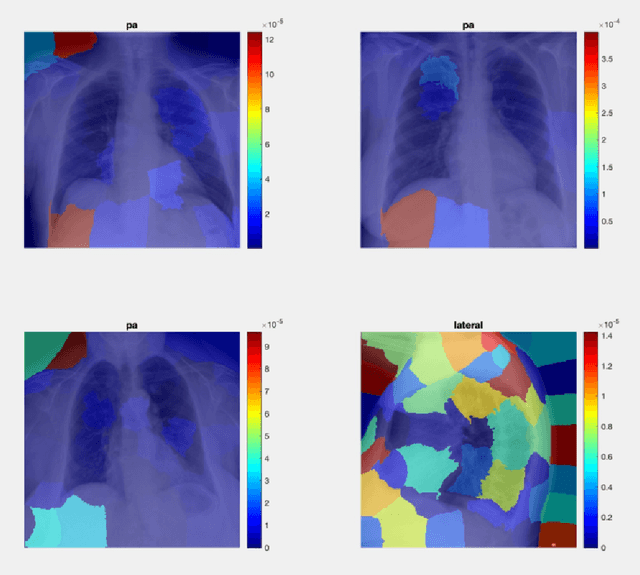
Explainable artificial intelligence (XAI) plays an indispensable role in demystifying the decision-making processes of AI, especially within the healthcare industry. Clinicians rely heavily on detailed reasoning when making a diagnosis, often CT scans for specific features that distinguish between benign and malignant lesions. A comprehensive diagnostic approach includes an evaluation of imaging results, patient observations, and clinical tests. The surge in deploying deep learning models as support systems in medical diagnostics has been significant, offering advances that traditional methods could not. However, the complexity and opacity of these models present a double-edged sword. As they operate as "black boxes," with their reasoning obscured and inaccessible, there's an increased risk of misdiagnosis, which can lead to patient harm. Hence, there is a pressing need to cultivate transparency within AI systems, ensuring that the rationale behind an AI's diagnostic recommendations is clear and understandable to medical practitioners. This shift towards transparency is not just beneficial -- it's a critical step towards responsible AI integration in healthcare, ensuring that AI aids rather than hinders medical professionals in their crucial work.

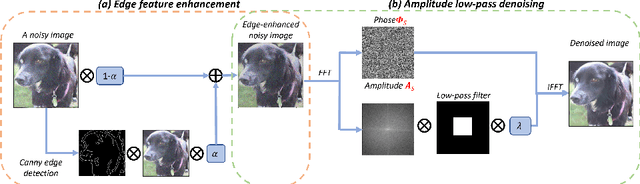
A Spectrum-based Image Denoising Method with Edge Feature Enhancement

Image denoising stands as a critical challenge in image processing and computer vision, aiming to restore the original image from noise-affected versions caused by various intrinsic and extrinsic factors. This process is essential for applications that rely on the high quality and clarity of visual information, such as image restoration, visual tracking, and image registration, where the original content is vital for performance. Despite the development of numerous denoising algorithms, effectively suppressing noise, particularly under poor capture conditions with high noise levels, remains a challenge. Image denoising's practical importance spans multiple domains, notably medical imaging for enhanced diagnostic precision, as well as surveillance and satellite imagery where it improves image quality and usability. Techniques like the Fourier transform, which excels in noise reduction and edge preservation, along with phase congruency-based methods, offer promising results for enhancing noisy and low-contrast images common in modern imaging scenarios.