Improving Stochastic Cubic Newton with Momentum

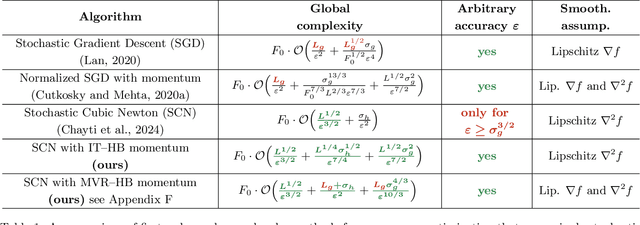
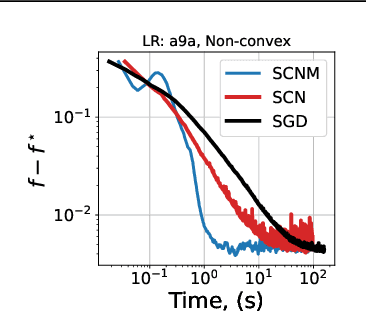
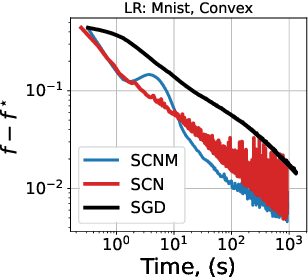
We study stochastic second-order methods for solving general non-convex optimization problems. We propose using a special version of momentum to stabilize the stochastic gradient and Hessian estimates in Newton's method. We show that momentum provably improves the variance of stochastic estimates and allows the method to converge for any noise level. Using the cubic regularization technique, we prove a global convergence rate for our method on general non-convex problems to a second-order stationary point, even when using only a single stochastic data sample per iteration. This starkly contrasts with all existing stochastic second-order methods for non-convex problems, which typically require large batches. Therefore, we are the first to demonstrate global convergence for batches of arbitrary size in the non-convex case for the Stochastic Cubic Newton. Additionally, we show improved speed on convex stochastic problems for our regularized Newton methods with momentum.

A New First-Order Meta-Learning Algorithm with Convergence Guarantees

Learning new tasks by drawing on prior experience gathered from other (related) tasks is a core property of any intelligent system. Gradient-based meta-learning, especially MAML and its variants, has emerged as a viable solution to accomplish this goal. One problem MAML encounters is its computational and memory burdens needed to compute the meta-gradients. We propose a new first-order variant of MAML that we prove converges to a stationary point of the MAML objective, unlike other first-order variants. We also show that the MAML objective does not satisfy the smoothness assumption assumed in previous works; we show instead that its smoothness constant grows with the norm of the meta-gradient, which theoretically suggests the use of normalized or clipped-gradient methods compared to the plain gradient method used in previous works. We validate our theory on a synthetic experiment.

Unified Convergence Theory of Stochastic and Variance-Reduced Cubic Newton Methods

We study the widely known Cubic-Newton method in the stochastic setting and propose a general framework to use variance reduction which we call the helper framework. In all previous work, these methods were proposed with very large batches (both in gradients and Hessians) and with various and often strong assumptions. In this work, we investigate the possibility of using such methods without large batches and use very simple assumptions that are sufficient for all our methods to work. In addition, we study these methods applied to gradient-dominated functions. In the general case, we show improved convergence (compared to first-order methods) to an approximate local minimum, and for gradient-dominated functions, we show convergence to approximate global minima.

Second-order optimization with lazy Hessians

We analyze Newton's method with lazy Hessian updates for solving general possibly non-convex optimization problems. We propose to reuse a previously seen Hessian for several iterations while computing new gradients at each step of the method. This significantly reduces the overall arithmetical complexity of second-order optimization schemes. By using the cubic regularization technique, we establish fast global convergence of our method to a second-order stationary point, while the Hessian does not need to be updated each iteration. For convex problems, we justify global and local superlinear rates for lazy Newton steps with quadratic regularization, which is easier to compute. The optimal frequency for updating the Hessian is once every $d$ iterations, where $d$ is the dimension of the problem. This provably improves the total arithmetical complexity of second-order algorithms by a factor $\sqrt{d}$.

Optimization with access to auxiliary information

We investigate the fundamental optimization question of minimizing a target function $f(x)$ whose gradients are expensive to compute or have limited availability, given access to some auxiliary side function $h(x)$ whose gradients are cheap or more available. This formulation captures many settings of practical relevance such as i) re-using batches in SGD, ii) transfer learning, iii) federated learning, iv) training with compressed models/dropout, etc. We propose two generic new algorithms which are applicable in all these settings and prove using only an assumption on the Hessian similarity between the target and side information that we can benefit from this framework.

Linear Speedup in Personalized Collaborative Learning

Personalization in federated learning can improve the accuracy of a model for a user by trading off the model's bias (introduced by using data from other users who are potentially different) against its variance (due to the limited amount of data on any single user). In order to develop training algorithms that optimally balance this trade-off, it is necessary to extend our theoretical foundations. In this work, we formalize the personalized collaborative learning problem as stochastic optimization of a user's objective $f_0(x)$ while given access to $N$ related but different objectives of other users $\{f_1(x), \dots, f_N(x)\}$. We give convergence guarantees for two algorithms in this setting -- a popular personalization method known as \emph{weighted gradient averaging}, and a novel \emph{bias correction} method -- and explore conditions under which we can optimally trade-off their bias for a reduction in variance and achieve linear speedup w.r.t.\ the number of users $N$. Further, we also empirically study their performance confirming our theoretical insights.