Loss Landscape Characterization of Neural Networks without Over-Parametrization
Paper and Code
Oct 17, 2024
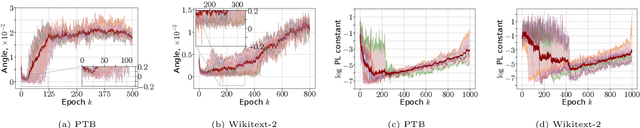

Optimization methods play a crucial role in modern machine learning, powering the remarkable empirical achievements of deep learning models. These successes are even more remarkable given the complex non-convex nature of the loss landscape of these models. Yet, ensuring the convergence of optimization methods requires specific structural conditions on the objective function that are rarely satisfied in practice. One prominent example is the widely recognized Polyak-Lojasiewicz (PL) inequality, which has gained considerable attention in recent years. However, validating such assumptions for deep neural networks entails substantial and often impractical levels of over-parametrization. In order to address this limitation, we propose a novel class of functions that can characterize the loss landscape of modern deep models without requiring extensive over-parametrization and can also include saddle points. Crucially, we prove that gradient-based optimizers possess theoretical guarantees of convergence under this assumption. Finally, we validate the soundness of our new function class through both theoretical analysis and empirical experimentation across a diverse range of deep learning models.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge