Physics-Informed Neural Networks for Multiphysics Data Assimilation with Application to Subsurface Transport

Data assimilation for parameter and state estimation in subsurface transport problems remains a significant challenge due to the sparsity of measurements, the heterogeneity of porous media, and the high computational cost of forward numerical models. We present a physics-informed deep neural networks (DNNs) machine learning method for estimating space-dependent hydraulic conductivity, hydraulic head, and concentration fields from sparse measurements. In this approach, we employ individual DNNs to approximate the unknown parameters (e.g., hydraulic conductivity) and states (e.g., hydraulic head and concentration) of a physical system, and jointly train these DNNs by minimizing the loss function that consists of the governing equations residuals in addition to the error with respect to measurement data. We apply this approach to assimilate conductivity, hydraulic head, and concentration measurements for joint inversion of the conductivity, hydraulic head, and concentration fields in a steady-state advection--dispersion problem. We study the accuracy of the physics-informed DNN approach with respect to data size, number of variables (conductivity and head versus conductivity, head, and concentration), DNNs size, and DNN initialization during training. We demonstrate that the physics-informed DNNs are significantly more accurate than standard data-driven DNNs when the training set consists of sparse data. We also show that the accuracy of parameter estimation increases as additional variables are inverted jointly.

Physics-Informed CoKriging: A Gaussian-Process-Regression-Based Multifidelity Method for Data-Model Convergence

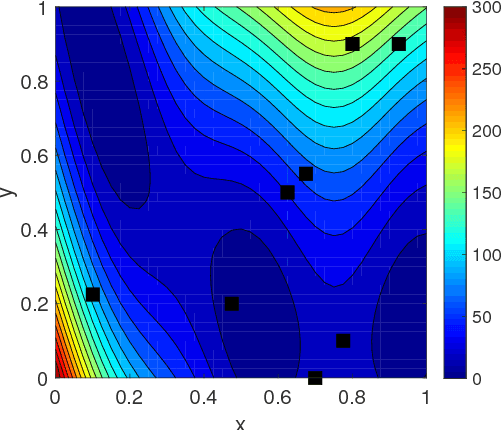
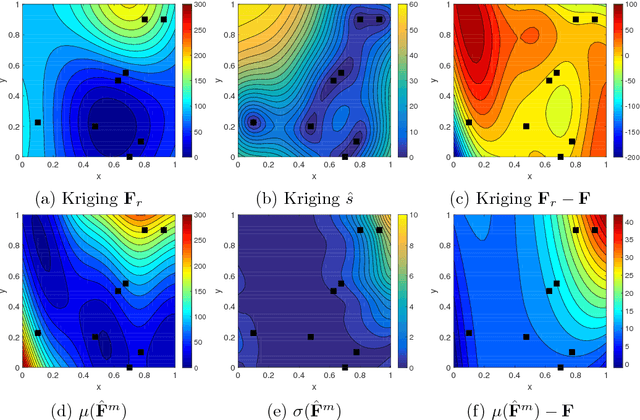
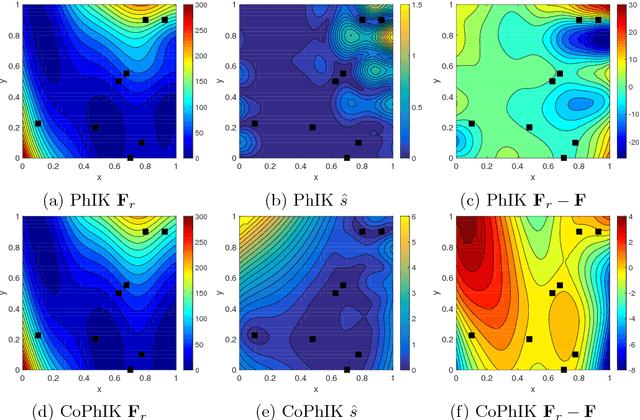
In this work, we propose a new Gaussian process regression (GPR)-based multifidelity method: physics-informed CoKriging (CoPhIK). In CoKriging-based multifidelity methods, the quantities of interest are modeled as linear combinations of multiple parameterized stationary Gaussian processes (GPs), and the hyperparameters of these GPs are estimated from data via optimization. In CoPhIK, we construct a GP representing low-fidelity data using physics-informed Kriging (PhIK), and model the discrepancy between low- and high-fidelity data using a parameterized GP with hyperparameters identified via optimization. Our approach reduces the cost of optimization for inferring hyperparameters by incorporating partial physical knowledge. We prove that the physical constraints in the form of deterministic linear operators are satisfied up to an error bound. Furthermore, we combine CoPhIK with a greedy active learning algorithm for guiding the selection of additional observation locations. The efficiency and accuracy of CoPhIK are demonstrated for reconstructing the partially observed modified Branin function, reconstructing the sparsely observed state of a steady state heat transport problem, and learning a conservative tracer distribution from sparse tracer concentration measurements.

Physics-Informed Kriging: A Physics-Informed Gaussian Process Regression Method for Data-Model Convergence

In this work, we propose a new Gaussian process regression (GPR) method: physics-informed Kriging (PhIK). In the standard data-driven Kriging, the unknown function of interest is usually treated as a Gaussian process with assumed stationary covariance with hyperparameters estimated from data. In PhIK, we compute the mean and covariance function from realizations of available stochastic models, e.g., from realizations of governing stochastic partial differential equations solutions. Such a constructed Gaussian process generally is non-stationary, and does not assume a specific form of the covariance function. Our approach avoids the costly optimization step in data-driven GPR methods to identify the hyperparameters. More importantly, we prove that the physical constraints in the form of a deterministic linear operator are guaranteed in the resulting prediction. We also provide an error estimate in preserving the physical constraints when errors are included in the stochastic model realizations. To reduce the computational cost of obtaining stochastic model realizations, we propose a multilevel Monte Carlo estimate of the mean and covariance functions. Further, we present an active learning algorithm that guides the selection of additional observation locations. The efficiency and accuracy of PhIK are demonstrated for reconstructing a partially known modified Branin function and learning a conservative tracer distribution from sparse concentration measurements.