Gaussian Process Regression with Soft Inequality and Monotonicity Constraints

Gaussian process (GP) regression is a non-parametric, Bayesian framework to approximate complex models. Standard GP regression can lead to an unbounded model in which some points can take infeasible values. We introduce a new GP method that enforces the physical constraints in a probabilistic manner. This GP model is trained by the quantum-inspired Hamiltonian Monte Carlo (QHMC). QHMC is an efficient way to sample from a broad class of distributions. Unlike the standard Hamiltonian Monte Carlo algorithm in which a particle has a fixed mass, QHMC allows a particle to have a random mass matrix with a probability distribution. Introducing the QHMC method to the inequality and monotonicity constrained GP regression in the probabilistic sense, our approach improves the accuracy and reduces the variance in the resulting GP model. According to our experiments on several datasets, the proposed approach serves as an efficient method as it accelerates the sampling process while maintaining the accuracy, and it is applicable to high dimensional problems.

Solving Seismic Wave Equations on Variable Velocity Models with Fourier Neural Operator

In the study of subsurface seismic imaging, solving the acoustic wave equation is a pivotal component in existing models. With the advancement of deep learning, neural networks are applied to numerically solve partial differential equations by learning the mapping between the inputs and the solution of the equation, the wave equation in particular, since traditional methods can be time consuming if numerous instances are to be solved. Previous works that concentrate on solving the wave equation by neural networks consider either a single velocity model or multiple simple velocity models, which is restricted in practice. Therefore, inspired by the idea of operator learning, this work leverages the Fourier neural operator (FNO) to effectively learn the frequency domain seismic wavefields under the context of variable velocity models. Moreover, we propose a new framework paralleled Fourier neural operator (PFNO) for efficiently training the FNO-based solver given multiple source locations and frequencies. Numerical experiments demonstrate the high accuracy of both FNO and PFNO with complicated velocity models in the OpenFWI datasets. Furthermore, the cross-dataset generalization test verifies that PFNO adapts to out-of-distribution velocity models. Also, PFNO has robust performance in the presence of random noise in the labels. Finally, PFNO admits higher computational efficiency on large-scale testing datasets, compared with the traditional finite-difference method. The aforementioned advantages endow the FNO-based solver with the potential to build powerful models for research on seismic waves.

Graphical Gaussian Process Regression Model for Aqueous Solvation Free Energy Prediction of Organic Molecules in Redox Flow Battery

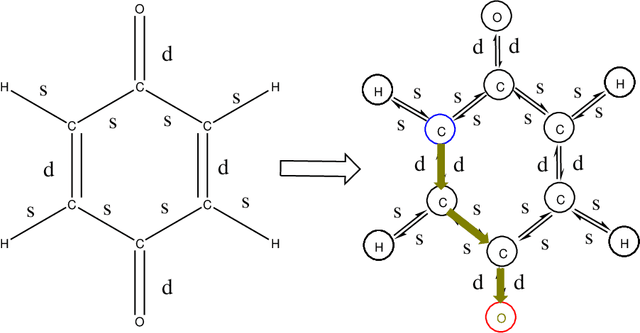
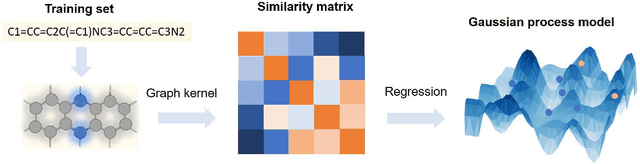
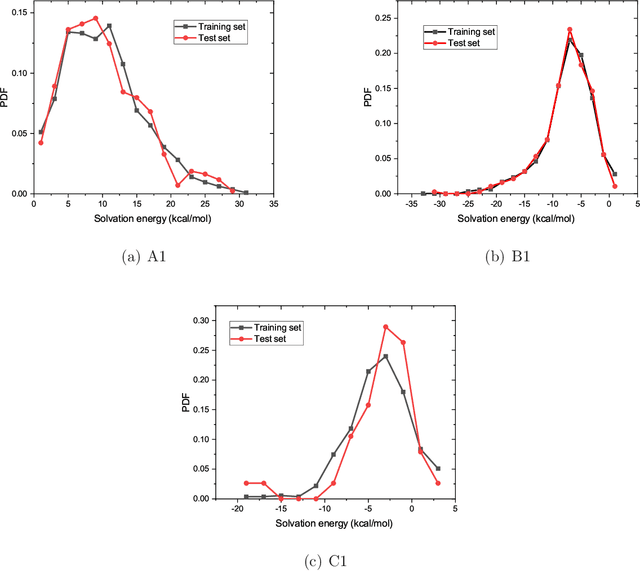
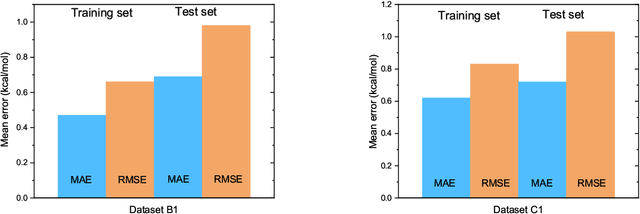
The solvation free energy of organic molecules is a critical parameter in determining emergent properties such as solubility, liquid-phase equilibrium constants, and pKa and redox potentials in an organic redox flow battery. In this work, we present a machine learning (ML) model that can learn and predict the aqueous solvation free energy of an organic molecule using Gaussian process regression method based on a new molecular graph kernel. To investigate the performance of the ML model on electrostatic interaction, the nonpolar interaction contribution of solvent and the conformational entropy of solute in solvation free energy, three data sets with implicit or explicit water solvent models, and contribution of conformational entropy of solute are tested. We demonstrate that our ML model can predict the solvation free energy of molecules at chemical accuracy with a mean absolute error of less than 1 kcal/mol for subsets of the QM9 dataset and the Freesolv database. To solve the general data scarcity problem for a graph-based ML model, we propose a dimension reduction algorithm based on the distance between molecular graphs, which can be used to examine the diversity of the molecular data set. It provides a promising way to build a minimum training set to improve prediction for certain test sets where the space of molecular structures is predetermined.

A Physics-Informed Neural Network Framework For Partial Differential Equations on 3D Surfaces: Time-Dependent Problems

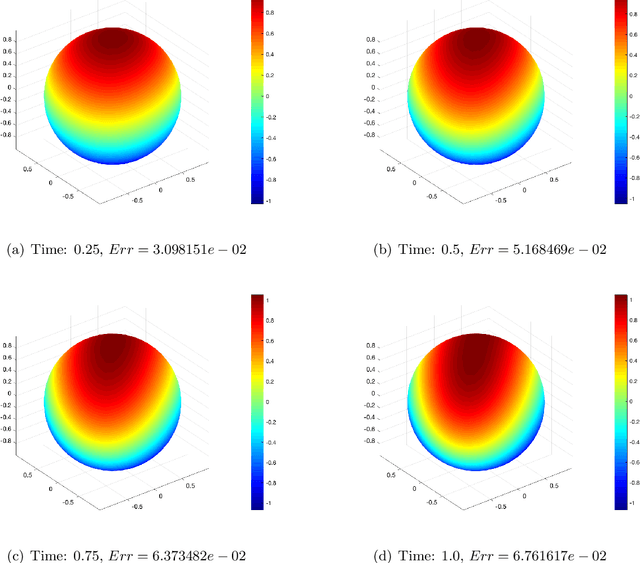
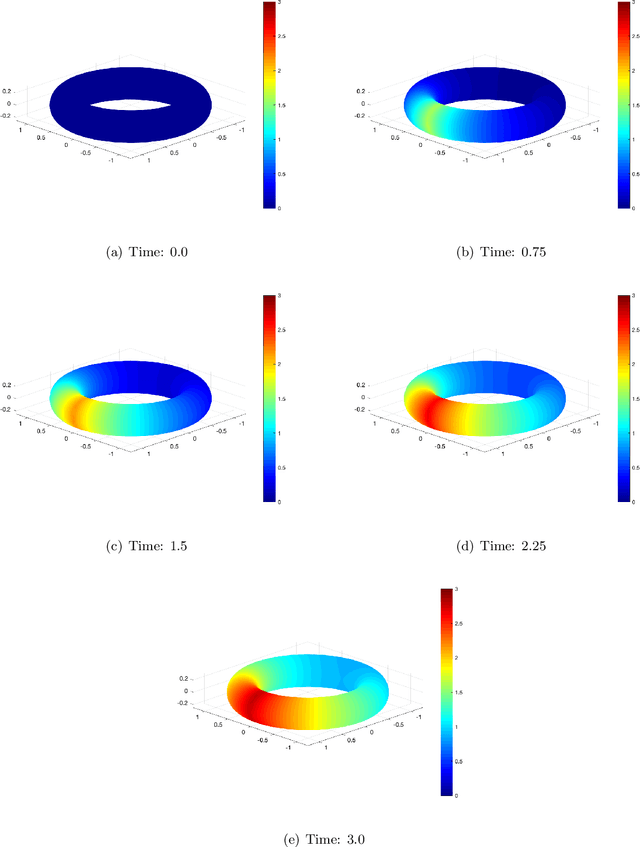
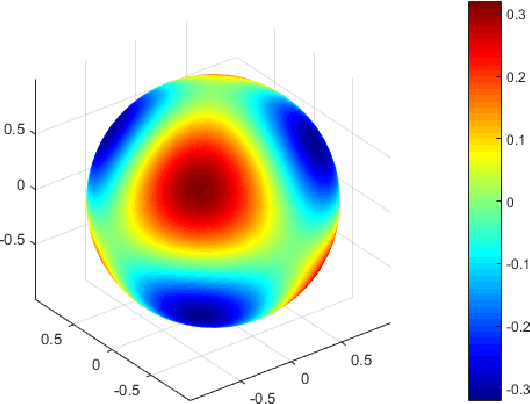
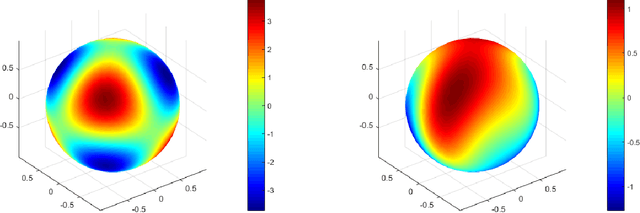
In this paper, we show a physics-informed neural network solver for the time-dependent surface PDEs. Unlike the traditional numerical solver, no extension of PDE and mesh on the surface is needed. We show a simplified prior estimate of the surface differential operators so that PINN's loss value will be an indicator of the residue of the surface PDEs. Numerical experiments verify efficacy of our algorithm.

Multifidelity Data Fusion via Gradient-Enhanced Gaussian Process Regression

We propose a data fusion method based on multi-fidelity Gaussian process regression (GPR) framework. This method combines available data of the quantity of interest (QoI) and its gradients with different fidelity levels, namely, it is a Gradient-enhanced Cokriging method (GE-Cokriging). It provides the approximations of both the QoI and its gradients simultaneously with uncertainty estimates. We compare this method with the conventional multi-fidelity Cokriging method that does not use gradients information, and the result suggests that GE-Cokriging has a better performance in predicting both QoI and its gradients. Moreover, GE-Cokriging even shows better generalization result in some cases where Cokriging performs poorly due to the singularity of the covariance matrix. We demonstrate the application of GE-Cokriging in several practical cases including reconstructing the trajectories and velocity of an underdamped oscillator with respect to time simultaneously, and investigating the sensitivity of power factor of a load bus with respect to varying power inputs of a generator bus in a large scale power system. We also show that though GE-Cokriging method requires a little bit higher computational cost than Cokriging method, the result of accuracy comparison shows that this cost is usually worth it.

Nonnegativity-Enforced Gaussian Process Regression

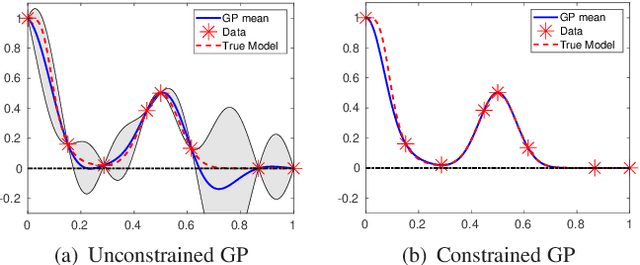
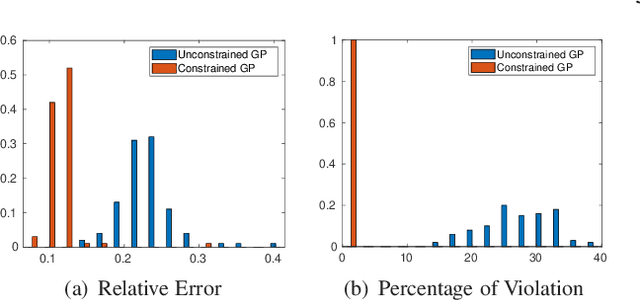
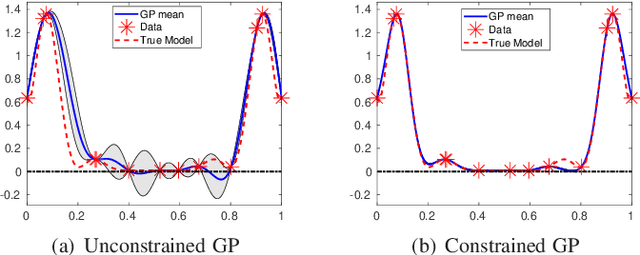
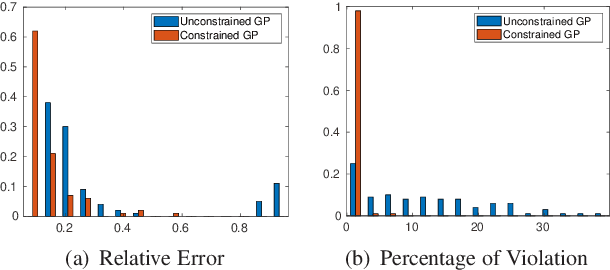
Gaussian Process (GP) regression is a flexible non-parametric approach to approximate complex models. In many cases, these models correspond to processes with bounded physical properties. Standard GP regression typically results in a proxy model which is unbounded for all temporal or spacial points, and thus leaves the possibility of taking on infeasible values. We propose an approach to enforce the physical constraints in a probabilistic way under the GP regression framework. In addition, this new approach reduces the variance in the resulting GP model.

When Bifidelity Meets CoKriging: An Efficient Physics-Informed Multifidelity Method

In this work, we propose a framework that combines the approximation-theory-based multifidelity method and Gaussian-process-regression-based multifidelity method to achieve data-model convergence when stochastic simulation models and sparse accurate observation data are available. Specifically, the two types of multifidelity methods we use are the bifidelity and CoKriging methods. The new approach uses the bifidelity method to efficiently estimate the empirical mean and covariance of the stochastic simulation outputs, then it uses these statistics to construct a Gaussian process (GP) representing low-fidelity in CoKriging. We also combine the bifidelity method with Kriging, where the approximated empirical statistics are used to construct the GP as well. We prove that the resulting posterior mean by the new physics-informed approach preserves linear physical constraints up to an error bound. By using this method, we can obtain an accurate construction of a state of interest based on a partially correct physical model and a few accurate observations. We present numerical examples to demonstrate performance of the method.

Physics-Informed CoKriging: A Gaussian-Process-Regression-Based Multifidelity Method for Data-Model Convergence

In this work, we propose a new Gaussian process regression (GPR)-based multifidelity method: physics-informed CoKriging (CoPhIK). In CoKriging-based multifidelity methods, the quantities of interest are modeled as linear combinations of multiple parameterized stationary Gaussian processes (GPs), and the hyperparameters of these GPs are estimated from data via optimization. In CoPhIK, we construct a GP representing low-fidelity data using physics-informed Kriging (PhIK), and model the discrepancy between low- and high-fidelity data using a parameterized GP with hyperparameters identified via optimization. Our approach reduces the cost of optimization for inferring hyperparameters by incorporating partial physical knowledge. We prove that the physical constraints in the form of deterministic linear operators are satisfied up to an error bound. Furthermore, we combine CoPhIK with a greedy active learning algorithm for guiding the selection of additional observation locations. The efficiency and accuracy of CoPhIK are demonstrated for reconstructing the partially observed modified Branin function, reconstructing the sparsely observed state of a steady state heat transport problem, and learning a conservative tracer distribution from sparse tracer concentration measurements.

Physics-Informed Kriging: A Physics-Informed Gaussian Process Regression Method for Data-Model Convergence

In this work, we propose a new Gaussian process regression (GPR) method: physics-informed Kriging (PhIK). In the standard data-driven Kriging, the unknown function of interest is usually treated as a Gaussian process with assumed stationary covariance with hyperparameters estimated from data. In PhIK, we compute the mean and covariance function from realizations of available stochastic models, e.g., from realizations of governing stochastic partial differential equations solutions. Such a constructed Gaussian process generally is non-stationary, and does not assume a specific form of the covariance function. Our approach avoids the costly optimization step in data-driven GPR methods to identify the hyperparameters. More importantly, we prove that the physical constraints in the form of a deterministic linear operator are guaranteed in the resulting prediction. We also provide an error estimate in preserving the physical constraints when errors are included in the stochastic model realizations. To reduce the computational cost of obtaining stochastic model realizations, we propose a multilevel Monte Carlo estimate of the mean and covariance functions. Further, we present an active learning algorithm that guides the selection of additional observation locations. The efficiency and accuracy of PhIK are demonstrated for reconstructing a partially known modified Branin function and learning a conservative tracer distribution from sparse concentration measurements.