FragNet: A Graph Neural Network for Molecular Property Prediction with Four Layers of Interpretability

Molecular property prediction is a crucial step in many modern-day scientific applications including drug discovery and energy storage material design. Despite the availability of numerous machine learning models for this task, we are lacking in models that provide both high accuracies and interpretability of the predictions. We introduce the FragNet architecture, a graph neural network not only capable of achieving prediction accuracies comparable to the current state-of-the-art models, but also able to provide insight on four levels of molecular substructures. This model enables understanding of which atoms, bonds, molecular fragments, and molecular fragment connections are critical in the prediction of a given molecular property. The ability to interpret the importance of connections between fragments is of particular interest for molecules which have substructures that are not connected with regular covalent bonds. The interpretable capabilities of FragNet are key to gaining scientific insights from the model's learned patterns between molecular structure and molecular properties.

Physics-informed machine learning of the correlation functions in bulk fluids

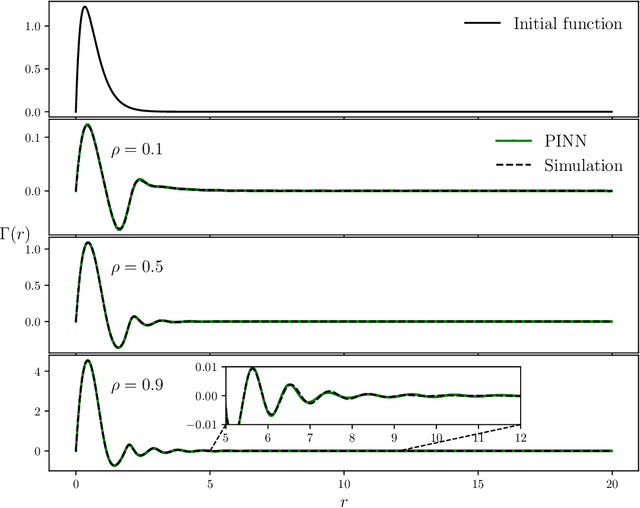
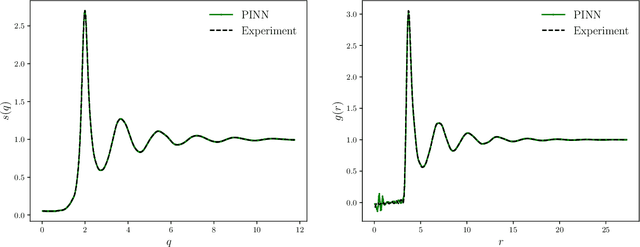
The Ornstein-Zernike (OZ) equation is the fundamental equation for pair correlation function computations in the modern integral equation theory for liquids. In this work, machine learning models, notably physics-informed neural networks and physics-informed neural operator networks, are explored to solve the OZ equation. The physics-informed machine learning models demonstrate great accuracy and high efficiency in solving the forward and inverse OZ problems of various bulk fluids. The results highlight the significant potential of physics-informed machine learning for applications in thermodynamic state theory.

Graphical Gaussian Process Regression Model for Aqueous Solvation Free Energy Prediction of Organic Molecules in Redox Flow Battery

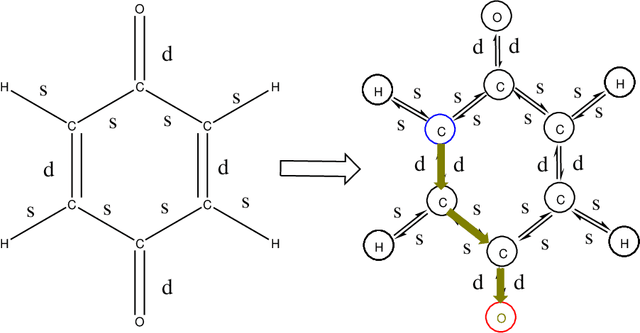
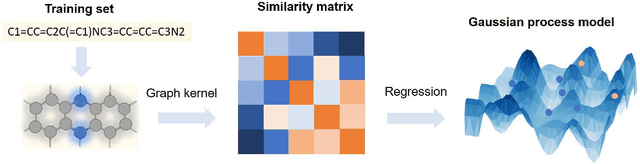
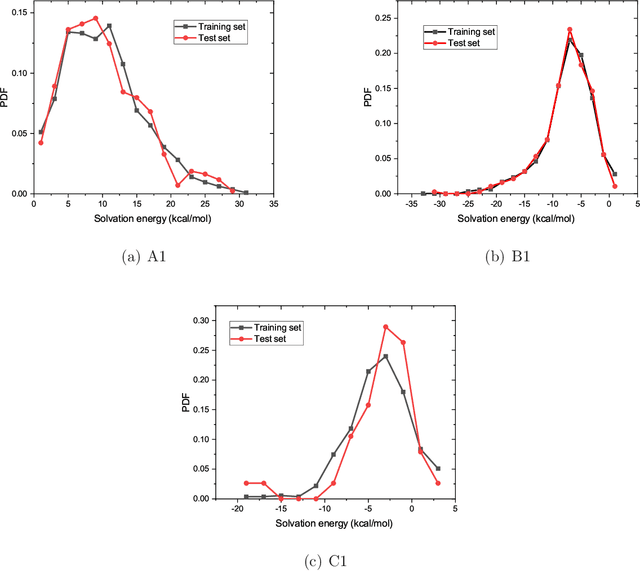
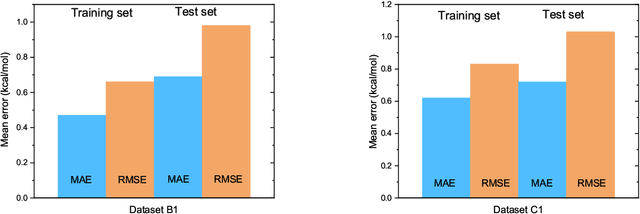
The solvation free energy of organic molecules is a critical parameter in determining emergent properties such as solubility, liquid-phase equilibrium constants, and pKa and redox potentials in an organic redox flow battery. In this work, we present a machine learning (ML) model that can learn and predict the aqueous solvation free energy of an organic molecule using Gaussian process regression method based on a new molecular graph kernel. To investigate the performance of the ML model on electrostatic interaction, the nonpolar interaction contribution of solvent and the conformational entropy of solute in solvation free energy, three data sets with implicit or explicit water solvent models, and contribution of conformational entropy of solute are tested. We demonstrate that our ML model can predict the solvation free energy of molecules at chemical accuracy with a mean absolute error of less than 1 kcal/mol for subsets of the QM9 dataset and the Freesolv database. To solve the general data scarcity problem for a graph-based ML model, we propose a dimension reduction algorithm based on the distance between molecular graphs, which can be used to examine the diversity of the molecular data set. It provides a promising way to build a minimum training set to improve prediction for certain test sets where the space of molecular structures is predetermined.