Permutation-Consensus Listwise Judging for Robust Factuality Evaluation

Large language models (LLMs) are now widely used as judges, yet their decisions can change under presentation choices that should be irrelevant. We study one such source of instability: candidate-order sensitivity in listwise factuality evaluation, where several answers can look similarly polished while differing sharply in hallucination risk. We introduce PCFJudge, an inference-time method that reruns the same factuality-first listwise prompt over multiple orderings of the same candidate set and aggregates the resulting scores, ranks, and uncertainty signals into a single consensus decision. On RewardBench 2 Factuality, PCFJudge improves over direct judging by up to 7 absolute points. Development ablations show that the dominant gain comes from permutation consensus itself rather than from heavier arbitration layers. These results suggest that a meaningful share of factuality-judging error arises from order instability, and that averaging over this nuisance variation is a simple and effective way to make LLM evaluation more reliable.

ArGEnT: Arbitrary Geometry-encoded Transformer for Operator Learning

Learning solution operators for systems with complex, varying geometries and parametric physical settings is a central challenge in scientific machine learning. In many-query regimes such as design optimization, control and inverse problems, surrogate modeling must generalize across geometries while allowing flexible evaluation at arbitrary spatial locations. In this work, we propose Arbitrary Geometry-encoded Transformer (ArGEnT), a geometry-aware attention-based architecture for operator learning on arbitrary domains. ArGEnT employs Transformer attention mechanisms to encode geometric information directly from point-cloud representations with three variants-self-attention, cross-attention, and hybrid-attention-that incorporates different strategies for incorporating geometric features. By integrating ArGEnT into DeepONet as the trunk network, we develop a surrogate modeling framework capable of learning operator mappings that depend on both geometric and non-geometric inputs without the need to explicitly parametrize geometry as a branch network input. Evaluation on benchmark problems spanning fluid dynamics, solid mechanics and electrochemical systems, we demonstrate significantly improved prediction accuracy and generalization performance compared with the standard DeepONet and other existing geometry-aware saurrogates. In particular, the cross-attention transformer variant enables accurate geometry-conditioned predictions with reduced reliance on signed distance functions. By combining flexible geometry encoding with operator-learning capabilities, ArGEnT provides a scalable surrogate modeling framework for optimization, uncertainty quantification, and data-driven modeling of complex physical systems.

Self-adaptive weighting and sampling for physics-informed neural networks

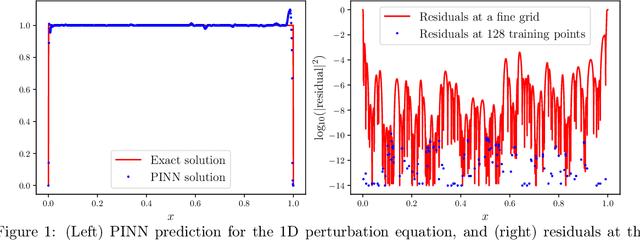
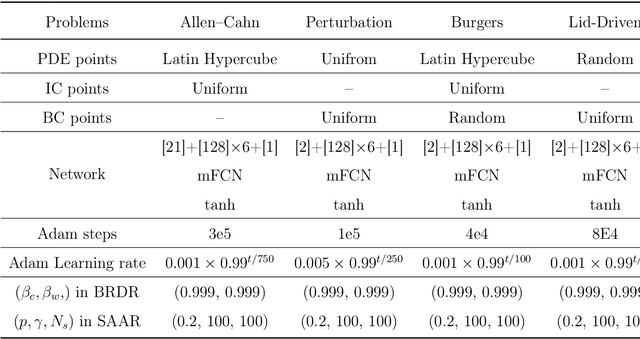
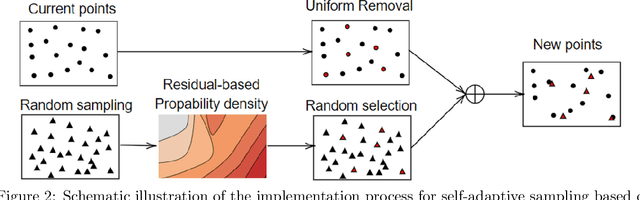
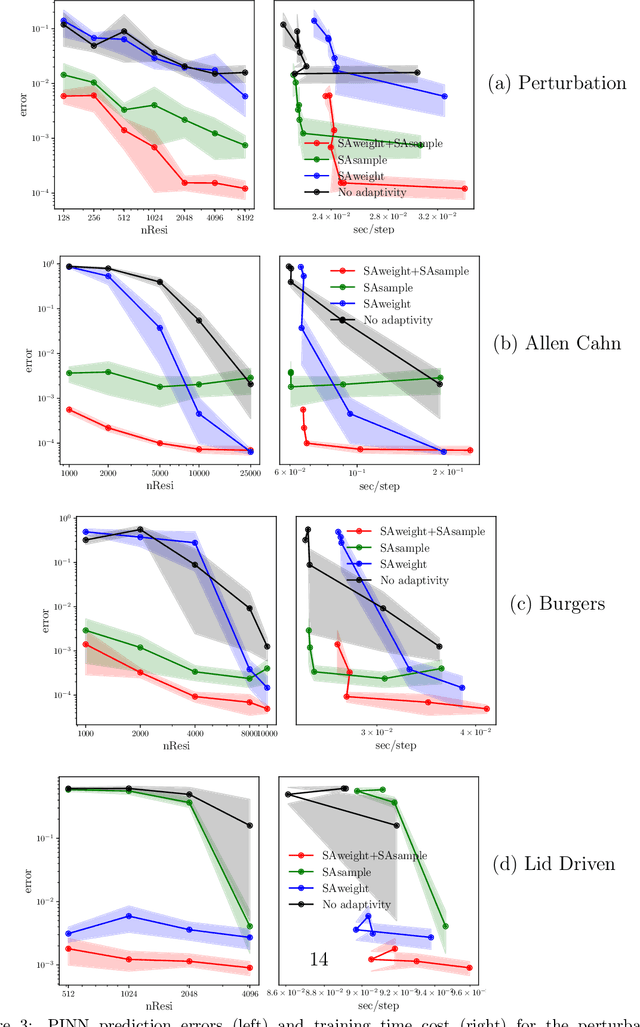
Physics-informed deep learning has emerged as a promising framework for solving partial differential equations (PDEs). Nevertheless, training these models on complex problems remains challenging, often leading to limited accuracy and efficiency. In this work, we introduce a hybrid adaptive sampling and weighting method to enhance the performance of physics-informed neural networks (PINNs). The adaptive sampling component identifies training points in regions where the solution exhibits rapid variation, while the adaptive weighting component balances the convergence rate across training points. Numerical experiments show that applying only adaptive sampling or only adaptive weighting is insufficient to consistently achieve accurate predictions, particularly when training points are scarce. Since each method emphasizes different aspects of the solution, their effectiveness is problem dependent. By combining both strategies, the proposed framework consistently improves prediction accuracy and training efficiency, offering a more robust approach for solving PDEs with PINNs.

Self-adaptive weights based on balanced residual decay rate for physics-informed neural networks and deep operator networks

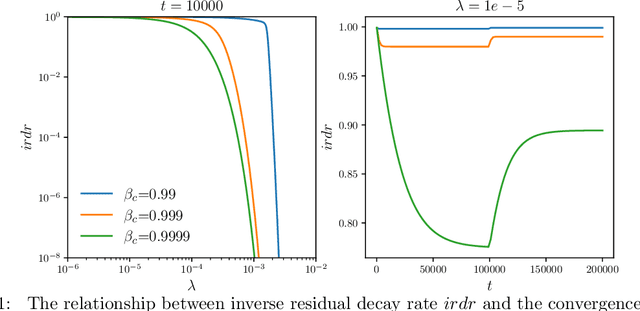
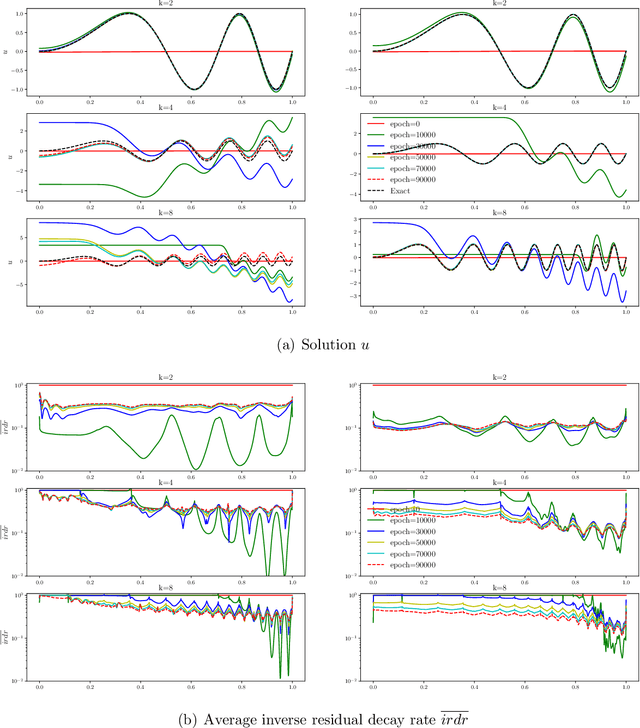
Physics-informed deep learning has emerged as a promising alternative for solving partial differential equations. However, for complex problems, training these networks can still be challenging, often resulting in unsatisfactory accuracy and efficiency. In this work, we demonstrate that the failure of plain physics-informed neural networks arises from the significant discrepancy in the convergence speed of residuals at different training points, where the slowest convergence speed dominates the overall solution convergence. Based on these observations, we propose a point-wise adaptive weighting method that balances the residual decay rate across different training points. The performance of our proposed adaptive weighting method is compared with current state-of-the-art adaptive weighting methods on benchmark problems for both physics-informed neural networks and physics-informed deep operator networks. Through extensive numerical results we demonstrate that our proposed approach of balanced residual decay rates offers several advantages, including bounded weights, high prediction accuracy, fast convergence speed, low training uncertainty, low computational cost and ease of hyperparameter tuning.

Physics-informed machine learning of the correlation functions in bulk fluids

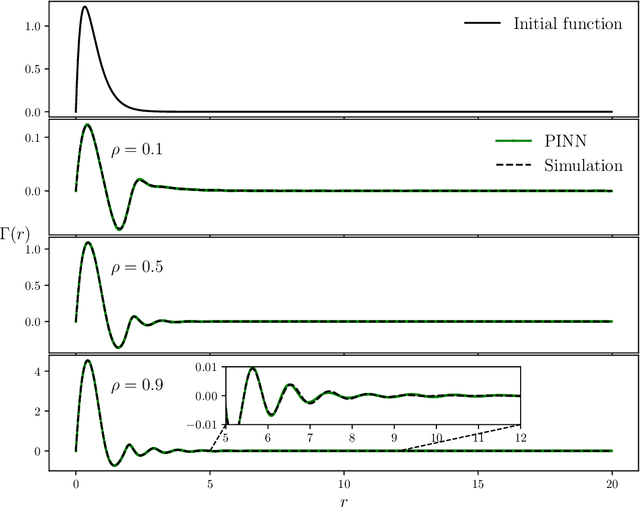
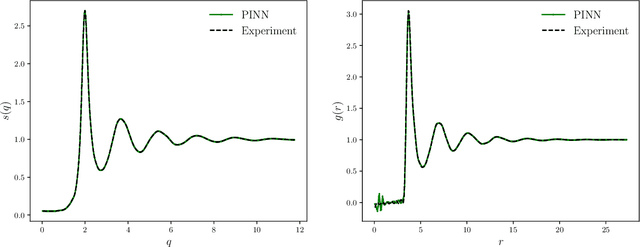
The Ornstein-Zernike (OZ) equation is the fundamental equation for pair correlation function computations in the modern integral equation theory for liquids. In this work, machine learning models, notably physics-informed neural networks and physics-informed neural operator networks, are explored to solve the OZ equation. The physics-informed machine learning models demonstrate great accuracy and high efficiency in solving the forward and inverse OZ problems of various bulk fluids. The results highlight the significant potential of physics-informed machine learning for applications in thermodynamic state theory.

Physics-informed machine learning of redox flow battery based on a two-dimensional unit cell model

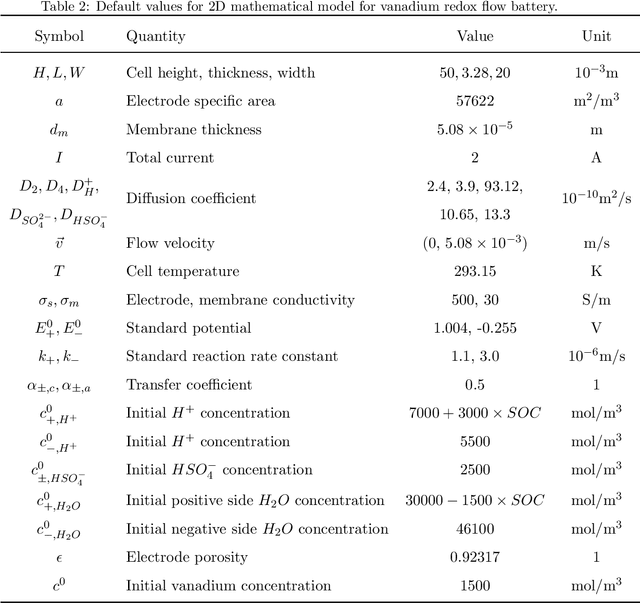
In this paper, we present a physics-informed neural network (PINN) approach for predicting the performance of an all-vanadium redox flow battery, with its physics constraints enforced by a two-dimensional (2D) mathematical model. The 2D model, which includes 6 governing equations and 24 boundary conditions, provides a detailed representation of the electrochemical reactions, mass transport and hydrodynamics occurring inside the redox flow battery. To solve the 2D model with the PINN approach, a composite neural network is employed to approximate species concentration and potentials; the input and output are normalized according to prior knowledge of the battery system; the governing equations and boundary conditions are first scaled to an order of magnitude around 1, and then further balanced with a self-weighting method. Our numerical results show that the PINN is able to predict cell voltage correctly, but the prediction of potentials shows a constant-like shift. To fix the shift, the PINN is enhanced by further constrains derived from the current collector boundary. Finally, we show that the enhanced PINN can be even further improved if a small number of labeled data is available.

Feature-adjacent multi-fidelity physics-informed machine learning for partial differential equations

Physics-informed neural networks have emerged as an alternative method for solving partial differential equations. However, for complex problems, the training of such networks can still require high-fidelity data which can be expensive to generate. To reduce or even eliminate the dependency on high-fidelity data, we propose a novel multi-fidelity architecture which is based on a feature space shared by the low- and high-fidelity solutions. In the feature space, the projections of the low-fidelity and high-fidelity solutions are adjacent by constraining their relative distance. The feature space is represented with an encoder and its mapping to the original solution space is effected through a decoder. The proposed multi-fidelity approach is validated on forward and inverse problems for steady and unsteady problems described by partial differential equations.