LanePtrNet: Revisiting Lane Detection as Point Voting and Grouping on Curves

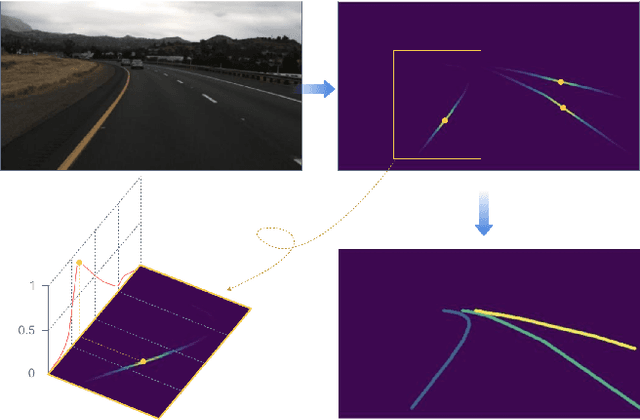
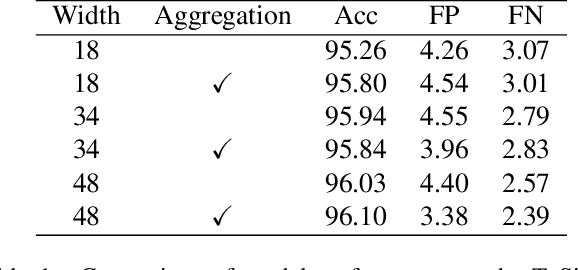
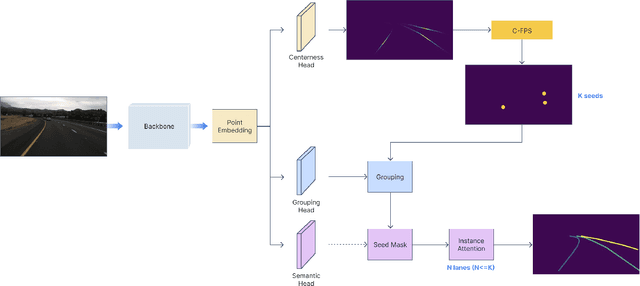
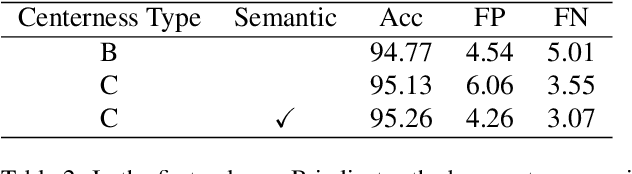
Lane detection plays a critical role in the field of autonomous driving. Prevailing methods generally adopt basic concepts (anchors, key points, etc.) from object detection and segmentation tasks, while these approaches require manual adjustments for curved objects, involve exhaustive searches on predefined anchors, require complex post-processing steps, and may lack flexibility when applied to real-world scenarios.In this paper, we propose a novel approach, LanePtrNet, which treats lane detection as a process of point voting and grouping on ordered sets: Our method takes backbone features as input and predicts a curve-aware centerness, which represents each lane as a point and assigns the most probable center point to it. A novel point sampling method is proposed to generate a set of candidate points based on the votes received. By leveraging features from local neighborhoods, and cross-instance attention score, we design a grouping module that further performs lane-wise clustering between neighboring and seeding points. Furthermore, our method can accommodate a point-based framework, (PointNet++ series, etc.) as an alternative to the backbone. This flexibility enables effortless extension to 3D lane detection tasks. We conduct comprehensive experiments to validate the effectiveness of our proposed approach, demonstrating its superior performance.

Uncertainty quantification for deeponets with ensemble kalman inversion

In recent years, operator learning, particularly the DeepONet, has received much attention for efficiently learning complex mappings between input and output functions across diverse fields. However, in practical scenarios with limited and noisy data, accessing the uncertainty in DeepONet predictions becomes essential, especially in mission-critical or safety-critical applications. Existing methods, either computationally intensive or yielding unsatisfactory uncertainty quantification, leave room for developing efficient and informative uncertainty quantification (UQ) techniques tailored for DeepONets. In this work, we proposed a novel inference approach for efficient UQ for operator learning by harnessing the power of the Ensemble Kalman Inversion (EKI) approach. EKI, known for its derivative-free, noise-robust, and highly parallelizable feature, has demonstrated its advantages for UQ for physics-informed neural networks [28]. Our innovative application of EKI enables us to efficiently train ensembles of DeepONets while obtaining informative uncertainty estimates for the output of interest. We deploy a mini-batch variant of EKI to accommodate larger datasets, mitigating the computational demand due to large datasets during the training stage. Furthermore, we introduce a heuristic method to estimate the artificial dynamics covariance, thereby improving our uncertainty estimates. Finally, we demonstrate the effectiveness and versatility of our proposed methodology across various benchmark problems, showcasing its potential to address the pressing challenges of uncertainty quantification in DeepONets, especially for practical applications with limited and noisy data.

Efficient Bayesian Physics Informed Neural Networks for Inverse Problems via Ensemble Kalman Inversion

Bayesian Physics Informed Neural Networks (B-PINNs) have gained significant attention for inferring physical parameters and learning the forward solutions for problems based on partial differential equations. However, the overparameterized nature of neural networks poses a computational challenge for high-dimensional posterior inference. Existing inference approaches, such as particle-based or variance inference methods, are either computationally expensive for high-dimensional posterior inference or provide unsatisfactory uncertainty estimates. In this paper, we present a new efficient inference algorithm for B-PINNs that uses Ensemble Kalman Inversion (EKI) for high-dimensional inference tasks. We find that our proposed method can achieve inference results with informative uncertainty estimates comparable to Hamiltonian Monte Carlo (HMC)-based B-PINNs with a much reduced computational cost. These findings suggest that our proposed approach has great potential for uncertainty quantification in physics-informed machine learning for practical applications.

Asymptotic-Preserving Neural Networks for multiscale hyperbolic models of epidemic spread

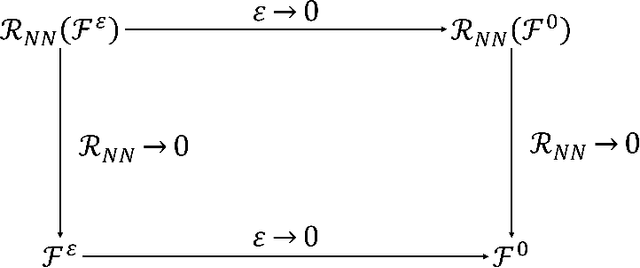
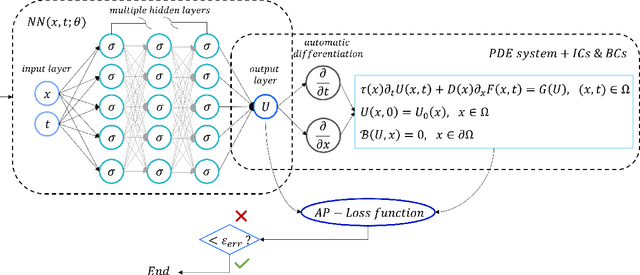
When investigating epidemic dynamics through differential models, the parameters needed to understand the phenomenon and to simulate forecast scenarios require a delicate calibration phase, often made even more challenging by the scarcity and uncertainty of the observed data reported by official sources. In this context, Physics-Informed Neural Networks (PINNs), by embedding the knowledge of the differential model that governs the physical phenomenon in the learning process, can effectively address the inverse and forward problem of data-driven learning and solving the corresponding epidemic problem. In many circumstances, however, the spatial propagation of an infectious disease is characterized by movements of individuals at different scales governed by multiscale PDEs. This reflects the heterogeneity of a region or territory in relation to the dynamics within cities and in neighboring zones. In presence of multiple scales, a direct application of PINNs generally leads to poor results due to the multiscale nature of the differential model in the loss function of the neural network. To allow the neural network to operate uniformly with respect to the small scales, it is desirable that the neural network satisfies an Asymptotic-Preservation (AP) property in the learning process. To this end, we consider a new class of AP Neural Networks (APNNs) for multiscale hyperbolic transport models of epidemic spread that, thanks to an appropriate AP formulation of the loss function, is capable to work uniformly at the different scales of the system. A series of numerical tests for different epidemic scenarios confirms the validity of the proposed approach, highlighting the importance of the AP property in the neural network when dealing with multiscale problems especially in presence of sparse and partially observed systems.

Nonnegativity-Enforced Gaussian Process Regression

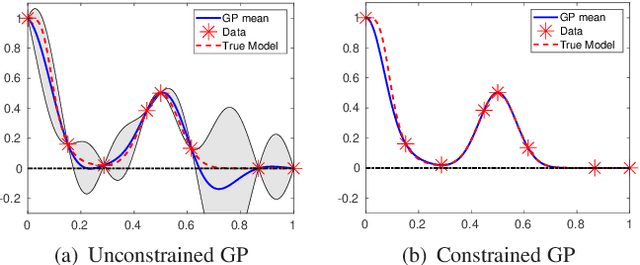
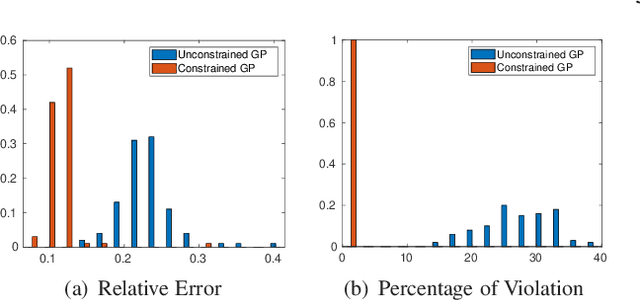
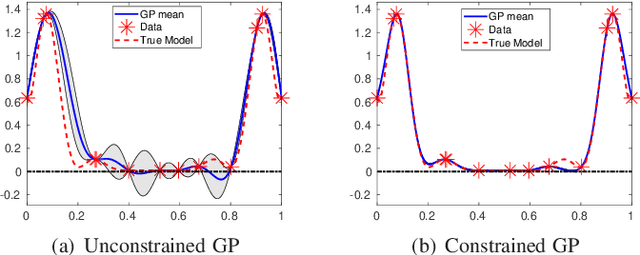
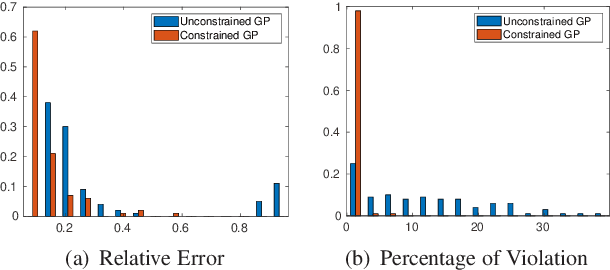
Gaussian Process (GP) regression is a flexible non-parametric approach to approximate complex models. In many cases, these models correspond to processes with bounded physical properties. Standard GP regression typically results in a proxy model which is unbounded for all temporal or spacial points, and thus leaves the possibility of taking on infeasible values. We propose an approach to enforce the physical constraints in a probabilistic way under the GP regression framework. In addition, this new approach reduces the variance in the resulting GP model.

Bifidelity data-assisted neural networks in nonintrusive reduced-order modeling

In this paper, we present a new nonintrusive reduced basis method when a cheap low-fidelity model and expensive high-fidelity model are available. The method relies on proper orthogonal decomposition (POD) to generate the high-fidelity reduced basis and a shallow multilayer perceptron to learn the high-fidelity reduced coefficients. In contrast to other methods, one distinct feature of the proposed method is to incorporate the features extracted from the low-fidelity data as the input feature, this approach not only improves the predictive capability of the neural network but also enables the decoupling the high-fidelity simulation from the online stage. Due to its nonintrusive nature, it is applicable to general parameterized problems. We also provide several numerical examples to illustrate the effectiveness and performance of the proposed method.

When Bifidelity Meets CoKriging: An Efficient Physics-Informed Multifidelity Method

In this work, we propose a framework that combines the approximation-theory-based multifidelity method and Gaussian-process-regression-based multifidelity method to achieve data-model convergence when stochastic simulation models and sparse accurate observation data are available. Specifically, the two types of multifidelity methods we use are the bifidelity and CoKriging methods. The new approach uses the bifidelity method to efficiently estimate the empirical mean and covariance of the stochastic simulation outputs, then it uses these statistics to construct a Gaussian process (GP) representing low-fidelity in CoKriging. We also combine the bifidelity method with Kriging, where the approximated empirical statistics are used to construct the GP as well. We prove that the resulting posterior mean by the new physics-informed approach preserves linear physical constraints up to an error bound. By using this method, we can obtain an accurate construction of a state of interest based on a partially correct physical model and a few accurate observations. We present numerical examples to demonstrate performance of the method.