When Bifidelity Meets CoKriging: An Efficient Physics-Informed Multifidelity Method
Paper and Code
Dec 07, 2018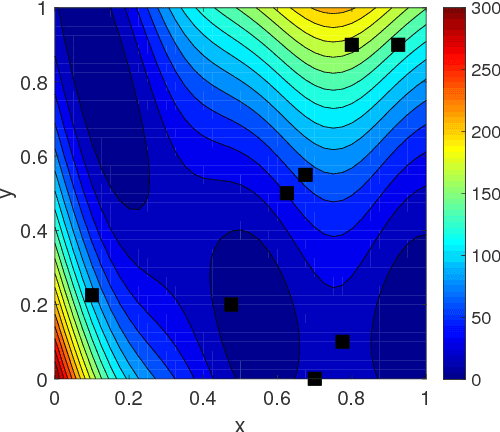
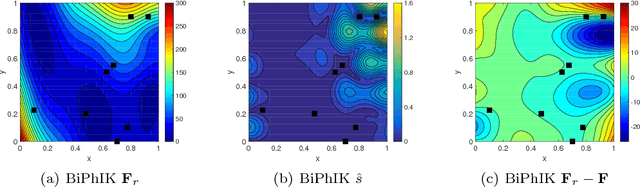
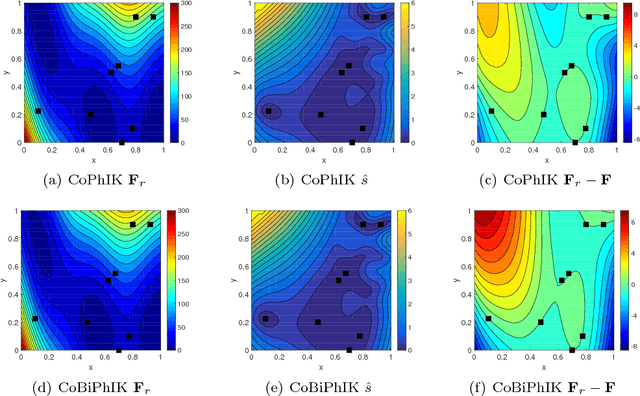
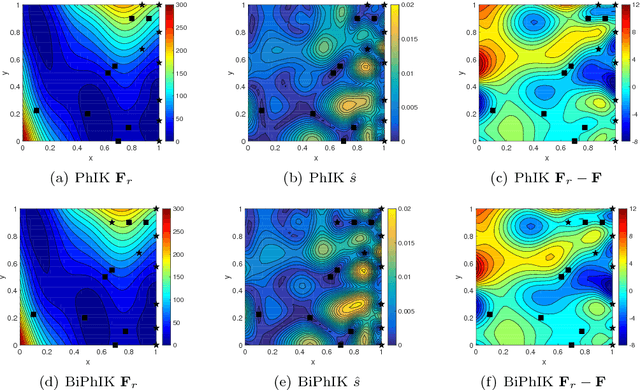
In this work, we propose a framework that combines the approximation-theory-based multifidelity method and Gaussian-process-regression-based multifidelity method to achieve data-model convergence when stochastic simulation models and sparse accurate observation data are available. Specifically, the two types of multifidelity methods we use are the bifidelity and CoKriging methods. The new approach uses the bifidelity method to efficiently estimate the empirical mean and covariance of the stochastic simulation outputs, then it uses these statistics to construct a Gaussian process (GP) representing low-fidelity in CoKriging. We also combine the bifidelity method with Kriging, where the approximated empirical statistics are used to construct the GP as well. We prove that the resulting posterior mean by the new physics-informed approach preserves linear physical constraints up to an error bound. By using this method, we can obtain an accurate construction of a state of interest based on a partially correct physical model and a few accurate observations. We present numerical examples to demonstrate performance of the method.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge