Micro-Macro Tensor Neural Surrogates for Uncertainty Quantification in Collisional Plasma

Plasma kinetic equations exhibit pronounced sensitivity to microscopic perturbations in model parameters and data, making reliable and efficient uncertainty quantification (UQ) essential for predictive simulations. However, the cost of uncertainty sampling, the high-dimensional phase space, and multiscale stiffness pose severe challenges to both computational efficiency and error control in traditional numerical methods. These aspects are further emphasized in presence of collisions where the high-dimensional nonlocal collision integrations and conservation properties pose severe constraints. To overcome this, we present a variance-reduced Monte Carlo framework for UQ in the Vlasov--Poisson--Landau (VPL) system, in which neural network surrogates replace the multiple costly evaluations of the Landau collision term. The method couples a high-fidelity, asymptotic-preserving VPL solver with inexpensive, strongly correlated surrogates based on the Vlasov--Poisson--Fokker--Planck (VPFP) and Euler--Poisson (EP) equations. For the surrogate models, we introduce a generalization of the separable physics-informed neural network (SPINN), developing a class of tensor neural networks based on an anisotropic micro-macro decomposition, to reduce velocity-moment costs, model complexity, and the curse of dimensionality. To further increase correlation with VPL, we calibrate the VPFP model and design an asymptotic-preserving SPINN whose small- and large-Knudsen limits recover the EP and VP systems, respectively. Numerical experiments show substantial variance reduction over standard Monte Carlo, accurate statistics with far fewer high-fidelity samples, and lower wall-clock time, while maintaining robustness to stochastic dimension.

Structure and asymptotic preserving deep neural surrogates for uncertainty quantification in multiscale kinetic equations

The high dimensionality of kinetic equations with stochastic parameters poses major computational challenges for uncertainty quantification (UQ). Traditional Monte Carlo (MC) sampling methods, while widely used, suffer from slow convergence and high variance, which become increasingly severe as the dimensionality of the parameter space grows. To accelerate MC sampling, we adopt a multiscale control variates strategy that leverages low-fidelity solutions from simplified kinetic models to reduce variance. To further improve sampling efficiency and preserve the underlying physics, we introduce surrogate models based on structure and asymptotic preserving neural networks (SAPNNs). These deep neural networks are specifically designed to satisfy key physical properties, including positivity, conservation laws, entropy dissipation, and asymptotic limits. By training the SAPNNs on low-fidelity models and enriching them with selected high-fidelity samples from the full Boltzmann equation, our method achieves significant variance reduction while maintaining physical consistency and asymptotic accuracy. The proposed methodology enables efficient large-scale prediction in kinetic UQ and is validated across both homogeneous and nonhomogeneous multiscale regimes. Numerical results demonstrate improved accuracy and computational efficiency compared to standard MC techniques.

A data augmentation strategy for deep neural networks with application to epidemic modelling

In this work, we integrate the predictive capabilities of compartmental disease dynamics models with machine learning ability to analyze complex, high-dimensional data and uncover patterns that conventional models may overlook. Specifically, we present a proof of concept demonstrating the application of data-driven methods and deep neural networks to a recently introduced SIR-type model with social features, including a saturated incidence rate, to improve epidemic prediction and forecasting. Our results show that a robust data augmentation strategy trough suitable data-driven models can improve the reliability of Feed-Forward Neural Networks (FNNs) and Nonlinear Autoregressive Networks (NARs), making them viable alternatives to Physics-Informed Neural Networks (PINNs). This approach enhances the ability to handle nonlinear dynamics and offers scalable, data-driven solutions for epidemic forecasting, prioritizing predictive accuracy over the constraints of physics-based models. Numerical simulations of the post-lockdown phase of the COVID-19 epidemic in Italy and Spain validate our methodology.

Asymptotic-Preserving Neural Networks for multiscale hyperbolic models of epidemic spread

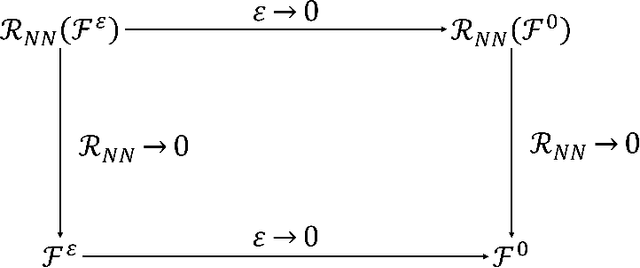
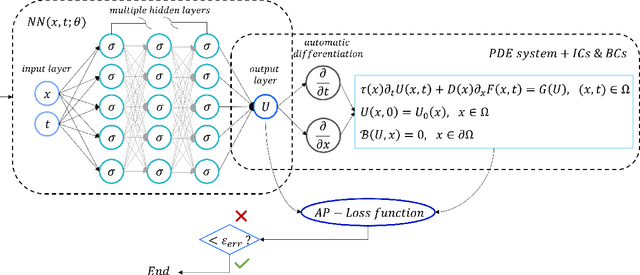
When investigating epidemic dynamics through differential models, the parameters needed to understand the phenomenon and to simulate forecast scenarios require a delicate calibration phase, often made even more challenging by the scarcity and uncertainty of the observed data reported by official sources. In this context, Physics-Informed Neural Networks (PINNs), by embedding the knowledge of the differential model that governs the physical phenomenon in the learning process, can effectively address the inverse and forward problem of data-driven learning and solving the corresponding epidemic problem. In many circumstances, however, the spatial propagation of an infectious disease is characterized by movements of individuals at different scales governed by multiscale PDEs. This reflects the heterogeneity of a region or territory in relation to the dynamics within cities and in neighboring zones. In presence of multiple scales, a direct application of PINNs generally leads to poor results due to the multiscale nature of the differential model in the loss function of the neural network. To allow the neural network to operate uniformly with respect to the small scales, it is desirable that the neural network satisfies an Asymptotic-Preservation (AP) property in the learning process. To this end, we consider a new class of AP Neural Networks (APNNs) for multiscale hyperbolic transport models of epidemic spread that, thanks to an appropriate AP formulation of the loss function, is capable to work uniformly at the different scales of the system. A series of numerical tests for different epidemic scenarios confirms the validity of the proposed approach, highlighting the importance of the AP property in the neural network when dealing with multiscale problems especially in presence of sparse and partially observed systems.

From particle swarm optimization to consensus based optimization: stochastic modeling and mean-field limit

In this paper we consider a continuous description based on stochastic differential equations of the popular particle swarm optimization (PSO) process for solving global optimization problems and derive in the large particle limit the corresponding mean-field approximation based on Vlasov-Fokker-Planck-type equations. The disadvantage of memory effects induced by the need to store the local best position is overcome by the introduction of an additional differential equation describing the evolution of the local best. A regularization process for the global best permits to formally derive the respective mean-field description. Subsequently, in the small inertia limit, we compute the related macroscopic hydrodynamic equations that clarify the link with the recently introduced consensus based optimization (CBO) methods. Several numerical examples illustrate the mean field process, the small inertia limit and the potential of this general class of global optimization methods.

Consensus-based Optimization on the Sphere II: Convergence to Global Minimizers and Machine Learning

We present the implementation of a new stochastic Kuramoto-Vicsek-type model for global optimization of nonconvex functions on the sphere. This model belongs to the class of Consensus-Based Optimization. In fact, particles move on the sphere driven by a drift towards an instantaneous consensus point, which is computed as a convex combination of particle locations, weighted by the cost function according to Laplace's principle, and it represents an approximation to a global minimizer. The dynamics is further perturbed by a random vector field to favor exploration, whose variance is a function of the distance of the particles to the consensus point. In particular, as soon as the consensus is reached the stochastic component vanishes. The main results of this paper are about the proof of convergence of the numerical scheme to global minimizers provided conditions of well-preparation of the initial datum. The proof combines previous results of mean-field limit with a novel asymptotic analysis, and classical convergence results of numerical methods for SDE. We present several numerical experiments, which show that the algorithm proposed in the present paper scales well with the dimension and is extremely versatile. To quantify the performances of the new approach, we show that the algorithm is able to perform essentially as good as ad hoc state of the art methods in challenging problems in signal processing and machine learning, namely the phase retrieval problem and the robust subspace detection.

Consensus-Based Optimization on the Sphere I: Well-Posedness and Mean-Field Limit

We introduce a new stochastic Kuramoto-Vicsek-type model for global optimization of nonconvex functions on the sphere. This model belongs to the class of Consensus-Based Optimization methods. In fact, particles move on the sphere driven by a drift towards an instantaneous consensus point, computed as a convex combination of the particle locations weighted by the cost function according to Laplace's principle. The consensus point represents an approximation to a global minimizer. The dynamics is further perturbed by a random vector field to favor exploration, whose variance is a function of the distance of the particles to the consensus point. In particular, as soon as the consensus is reached, then the stochastic component vanishes. In this paper, we study the well-posedness of the model and we derive rigorously its mean-field approximation for large particle limit.