Adaptive Sampling Quasi-Newton Methods for Zeroth-Order Stochastic Optimization
Paper and Code
Sep 24, 2021
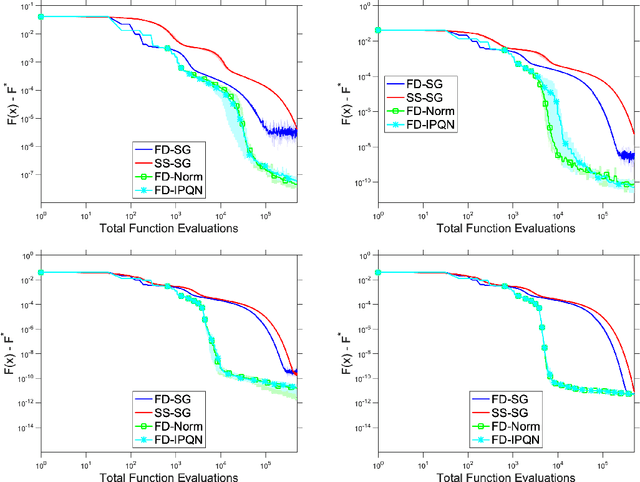
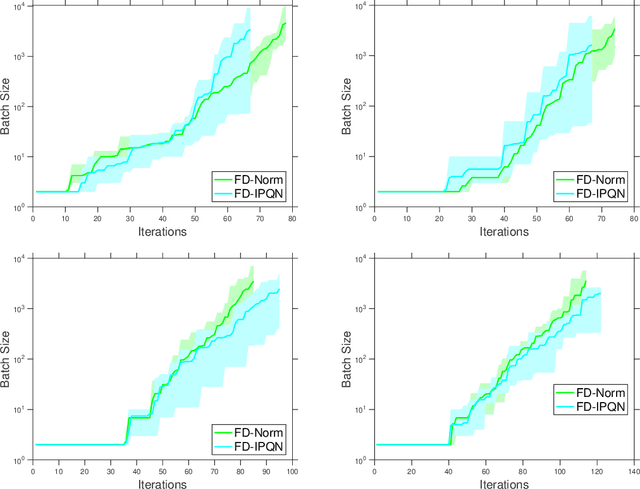
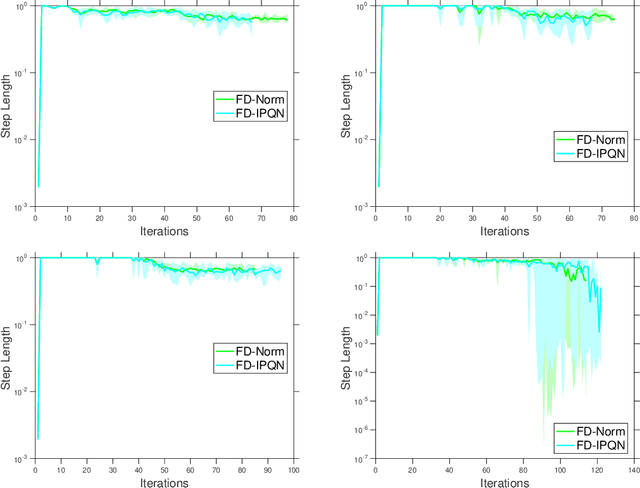
We consider unconstrained stochastic optimization problems with no available gradient information. Such problems arise in settings from derivative-free simulation optimization to reinforcement learning. We propose an adaptive sampling quasi-Newton method where we estimate the gradients of a stochastic function using finite differences within a common random number framework. We develop modified versions of a norm test and an inner product quasi-Newton test to control the sample sizes used in the stochastic approximations and provide global convergence results to the neighborhood of the optimal solution. We present numerical experiments on simulation optimization problems to illustrate the performance of the proposed algorithm. When compared with classical zeroth-order stochastic gradient methods, we observe that our strategies of adapting the sample sizes significantly improve performance in terms of the number of stochastic function evaluations required.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge