Importance of Kernel Bandwidth in Quantum Machine Learning

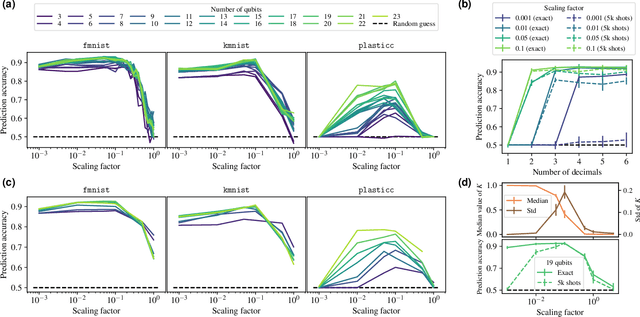
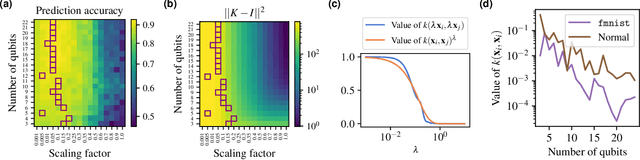
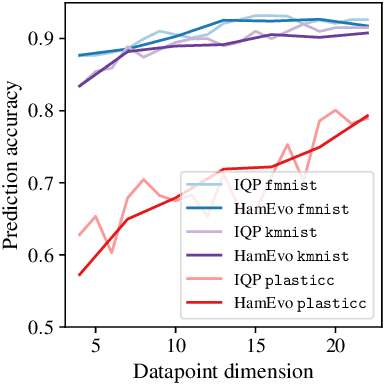
Quantum kernel methods are considered a promising avenue for applying quantum computers to machine learning problems. However, recent results overlook the central role hyperparameters play in determining the performance of machine learning methods. In this work we identify the hyperparameter controlling the bandwidth of a quantum kernel and show that it controls the expressivity of the resulting model. We use extensive numerical experiments with multiple quantum kernels and classical datasets to show consistent change in the model behavior from underfitting (bandwidth too large) to overfitting (bandwidth too small), with optimal generalization in between. We draw a connection between the bandwidth of classical and quantum kernels and show analogous behavior in both cases. Furthermore, we show that optimizing the bandwidth can help mitigate the exponential decay of kernel values with qubit count, which is the cause behind recent observations that the performance of quantum kernel methods decreases with qubit count. We reproduce these negative results and show that if the kernel bandwidth is optimized, the performance instead improves with growing qubit count and becomes competitive with the best classical methods.