Streetwise Agents: Empowering Offline RL Policies to Outsmart Exogenous Stochastic Disturbances in RTC

The difficulty of exploring and training online on real production systems limits the scope of real-time online data/feedback-driven decision making. The most feasible approach is to adopt offline reinforcement learning from limited trajectory samples. However, after deployment, such policies fail due to exogenous factors that temporarily or permanently disturb/alter the transition distribution of the assumed decision process structure induced by offline samples. This results in critical policy failures and generalization errors in sensitive domains like Real-Time Communication (RTC). We solve this crucial problem of identifying robust actions in presence of domain shifts due to unseen exogenous stochastic factors in the wild. As it is impossible to learn generalized offline policies within the support of offline data that are robust to these unseen exogenous disturbances, we propose a novel post-deployment shaping of policies (Streetwise), conditioned on real-time characterization of out-of-distribution sub-spaces. This leads to robust actions in bandwidth estimation (BWE) of network bottlenecks in RTC and in standard benchmarks. Our extensive experimental results on BWE and other standard offline RL benchmark environments demonstrate a significant improvement ($\approx$ 18% on some scenarios) in final returns wrt. end-user metrics over state-of-the-art baselines.

A Safe Reinforcement Learning Algorithm for Supervisory Control of Power Plants

Traditional control theory-based methods require tailored engineering for each system and constant fine-tuning. In power plant control, one often needs to obtain a precise representation of the system dynamics and carefully design the control scheme accordingly. Model-free Reinforcement learning (RL) has emerged as a promising solution for control tasks due to its ability to learn from trial-and-error interactions with the environment. It eliminates the need for explicitly modeling the environment's dynamics, which is potentially inaccurate. However, the direct imposition of state constraints in power plant control raises challenges for standard RL methods. To address this, we propose a chance-constrained RL algorithm based on Proximal Policy Optimization for supervisory control. Our method employs Lagrangian relaxation to convert the constrained optimization problem into an unconstrained objective, where trainable Lagrange multipliers enforce the state constraints. Our approach achieves the smallest distance of violation and violation rate in a load-follow maneuver for an advanced Nuclear Power Plant design.

Real-time Bandwidth Estimation from Offline Expert Demonstrations

In this work, we tackle the problem of bandwidth estimation (BWE) for real-time communication systems; however, in contrast to previous works, we leverage the vast efforts of prior heuristic-based BWE methods and synergize these approaches with deep learning-based techniques. Our work addresses challenges in generalizing to unseen network dynamics and extracting rich representations from prior experience, two key challenges in integrating data-driven bandwidth estimators into real-time systems. To that end, we propose Merlin, the first purely offline, data-driven solution to BWE that harnesses prior heuristic-based methods to extract an expert BWE policy. Through a series of experiments, we demonstrate that Merlin surpasses state-of-the-art heuristic-based and deep learning-based bandwidth estimators in terms of objective quality of experience metrics while generalizing beyond the offline world to in-the-wild network deployments where Merlin achieves a 42.85% and 12.8% reduction in packet loss and delay, respectively, when compared against WebRTC in inter-continental videoconferencing calls. We hope that Merlin's offline-oriented design fosters new strategies for real-time network control.

Numerical evidence against advantage with quantum fidelity kernels on classical data

Quantum machine learning techniques are commonly considered one of the most promising candidates for demonstrating practical quantum advantage. In particular, quantum kernel methods have been demonstrated to be able to learn certain classically intractable functions efficiently if the kernel is well-aligned with the target function. In the more general case, quantum kernels are known to suffer from exponential "flattening" of the spectrum as the number of qubits grows, preventing generalization and necessitating the control of the inductive bias by hyperparameters. We show that the general-purpose hyperparameter tuning techniques proposed to improve the generalization of quantum kernels lead to the kernel becoming well-approximated by a classical kernel, removing the possibility of quantum advantage. We provide extensive numerical evidence for this phenomenon utilizing multiple previously studied quantum feature maps and both synthetic and real data. Our results show that unless novel techniques are developed to control the inductive bias of quantum kernels, they are unlikely to provide a quantum advantage on classical data.

Multifidelity Reinforcement Learning with Control Variates

In many computational science and engineering applications, the output of a system of interest corresponding to a given input can be queried at different levels of fidelity with different costs. Typically, low-fidelity data is cheap and abundant, while high-fidelity data is expensive and scarce. In this work we study the reinforcement learning (RL) problem in the presence of multiple environments with different levels of fidelity for a given control task. We focus on improving the RL agent's performance with multifidelity data. Specifically, a multifidelity estimator that exploits the cross-correlations between the low- and high-fidelity returns is proposed to reduce the variance in the estimation of the state-action value function. The proposed estimator, which is based on the method of control variates, is used to design a multifidelity Monte Carlo RL (MFMCRL) algorithm that improves the learning of the agent in the high-fidelity environment. The impacts of variance reduction on policy evaluation and policy improvement are theoretically analyzed by using probability bounds. Our theoretical analysis and numerical experiments demonstrate that for a finite budget of high-fidelity data samples, our proposed MFMCRL agent attains superior performance compared with that of a standard RL agent that uses only the high-fidelity environment data for learning the optimal policy.

Learning-Based Distributed Random Access for Multi-Cell IoT Networks with NOMA

Non-orthogonal multiple access (NOMA) is a key technology to enable massive machine type communications (mMTC) in 5G networks and beyond. In this paper, NOMA is applied to improve the random access efficiency in high-density spatially-distributed multi-cell wireless IoT networks, where IoT devices contend for accessing the shared wireless channel using an adaptive p-persistent slotted Aloha protocol. To enable a capacity-optimal network, a novel formulation of random channel access with NOMA is proposed, in which the transmission probability of each IoT device is tuned to maximize the geometric mean of users' expected capacity. It is shown that the network optimization objective is high dimensional and mathematically intractable, yet it admits favourable mathematical properties that enable the design of efficient learning-based algorithmic solutions. To this end, two algorithms, i.e., a centralized model-based algorithm and a scalable distributed model-free algorithm, are proposed to optimally tune the transmission probabilities of IoT devices to attain the maximum capacity. The convergence of the proposed algorithms to the optimal solution is further established based on convex optimization and game-theoretic analysis. Extensive simulations demonstrate the merits of the novel formulation and the efficacy of the proposed algorithms.

A Gradient-Aware Search Algorithm for Constrained Markov Decision Processes

The canonical solution methodology for finite constrained Markov decision processes (CMDPs), where the objective is to maximize the expected infinite-horizon discounted rewards subject to the expected infinite-horizon discounted costs constraints, is based on convex linear programming. In this brief, we first prove that the optimization objective in the dual linear program of a finite CMDP is a piece-wise linear convex function (PWLC) with respect to the Lagrange penalty multipliers. Next, we propose a novel two-level Gradient-Aware Search (GAS) algorithm which exploits the PWLC structure to find the optimal state-value function and Lagrange penalty multipliers of a finite CMDP. The proposed algorithm is applied in two stochastic control problems with constraints: robot navigation in a grid world and solar-powered unmanned aerial vehicle (UAV)-based wireless network management. We empirically compare the convergence performance of the proposed GAS algorithm with binary search (BS), Lagrangian primal-dual optimization (PDO), and Linear Programming (LP). Compared with benchmark algorithms, it is shown that the proposed GAS algorithm converges to the optimal solution faster, does not require hyper-parameter tuning, and is not sensitive to initialization of the Lagrange penalty multiplier.

Constrained Deep Reinforcement Learning for Energy Sustainable Multi-UAV based Random Access IoT Networks with NOMA

In this paper, we apply the Non-Orthogonal Multiple Access (NOMA) technique to improve the massive channel access of a wireless IoT network where solar-powered Unmanned Aerial Vehicles (UAVs) relay data from IoT devices to remote servers. Specifically, IoT devices contend for accessing the shared wireless channel using an adaptive $p$-persistent slotted Aloha protocol; and the solar-powered UAVs adopt Successive Interference Cancellation (SIC) to decode multiple received data from IoT devices to improve access efficiency. To enable an energy-sustainable capacity-optimal network, we study the joint problem of dynamic multi-UAV altitude control and multi-cell wireless channel access management of IoT devices as a stochastic control problem with multiple energy constraints. To learn an optimal control policy, we first formulate this problem as a Constrained Markov Decision Process (CMDP), and propose an online model-free Constrained Deep Reinforcement Learning (CDRL) algorithm based on Lagrangian primal-dual policy optimization to solve the CMDP. Extensive simulations demonstrate that our proposed algorithm learns a cooperative policy among UAVs in which the altitude of UAVs and channel access probability of IoT devices are dynamically and jointly controlled to attain the maximal long-term network capacity while maintaining energy sustainability of UAVs. The proposed algorithm outperforms Deep RL based solutions with reward shaping to account for energy costs, and achieves a temporal average system capacity which is $82.4\%$ higher than that of a feasible DRL based solution, and only $6.47\%$ lower compared to that of the energy-constraint-free system.

Learning to Optimize Variational Quantum Circuits to Solve Combinatorial Problems

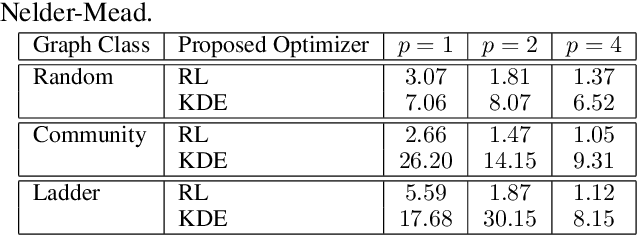
Quantum computing is a computational paradigm with the potential to outperform classical methods for a variety of problems. Proposed recently, the Quantum Approximate Optimization Algorithm (QAOA) is considered as one of the leading candidates for demonstrating quantum advantage in the near term. QAOA is a variational hybrid quantum-classical algorithm for approximately solving combinatorial optimization problems. The quality of the solution obtained by QAOA for a given problem instance depends on the performance of the classical optimizer used to optimize the variational parameters. In this paper, we formulate the problem of finding optimal QAOA parameters as a learning task in which the knowledge gained from solving training instances can be leveraged to find high-quality solutions for unseen test instances. To this end, we develop two machine-learning-based approaches. Our first approach adopts a reinforcement learning (RL) framework to learn a policy network to optimize QAOA circuits. Our second approach adopts a kernel density estimation (KDE) technique to learn a generative model of optimal QAOA parameters. In both approaches, the training procedure is performed on small-sized problem instances that can be simulated on a classical computer; yet the learned RL policy and the generative model can be used to efficiently solve larger problems. Extensive simulations using the IBM Qiskit Aer quantum circuit simulator demonstrate that our proposed RL- and KDE-based approaches reduce the optimality gap by factors up to 30.15 when compared with other commonly used off-the-shelf optimizers.

Reinforcement-Learning-Based Variational Quantum Circuits Optimization for Combinatorial Problems

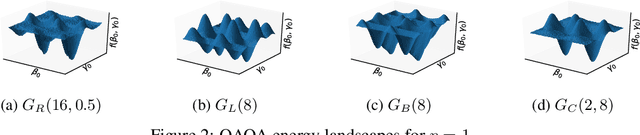
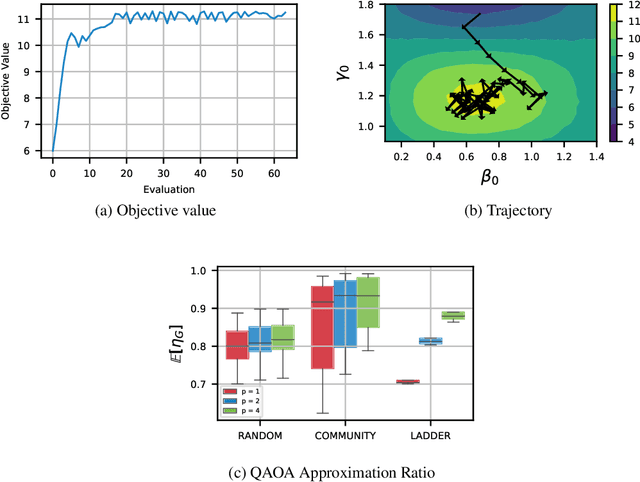
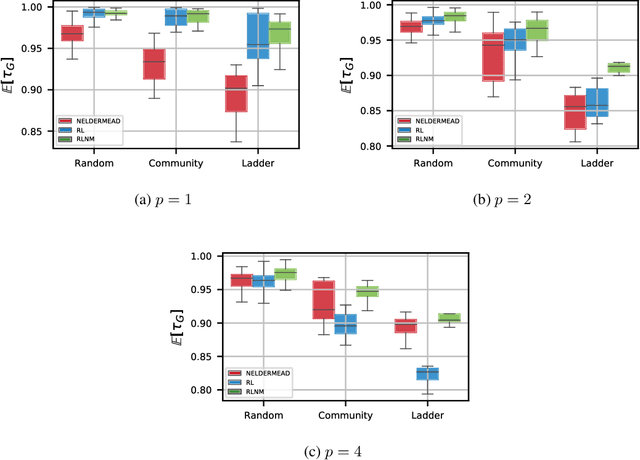
Quantum computing exploits basic quantum phenomena such as state superposition and entanglement to perform computations. The Quantum Approximate Optimization Algorithm (QAOA) is arguably one of the leading quantum algorithms that can outperform classical state-of-the-art methods in the near term. QAOA is a hybrid quantum-classical algorithm that combines a parameterized quantum state evolution with a classical optimization routine to approximately solve combinatorial problems. The quality of the solution obtained by QAOA within a fixed budget of calls to the quantum computer depends on the performance of the classical optimization routine used to optimize the variational parameters. In this work, we propose an approach based on reinforcement learning (RL) to train a policy network that can be used to quickly find high-quality variational parameters for unseen combinatorial problem instances. The RL agent is trained on small problem instances which can be simulated on a classical computer, yet the learned RL policy is generalizable and can be used to efficiently solve larger instances. Extensive simulations using the IBM Qiskit Aer quantum circuit simulator demonstrate that our trained RL policy can reduce the optimality gap by a factor up to 8.61 compared with other off-the-shelf optimizers tested.