Gregory Snyder
DeepAdversaries: Examining the Robustness of Deep Learning Models for Galaxy Morphology Classification
Dec 28, 2021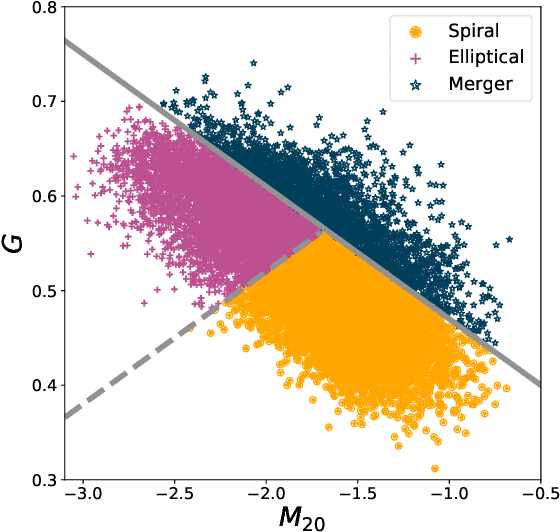
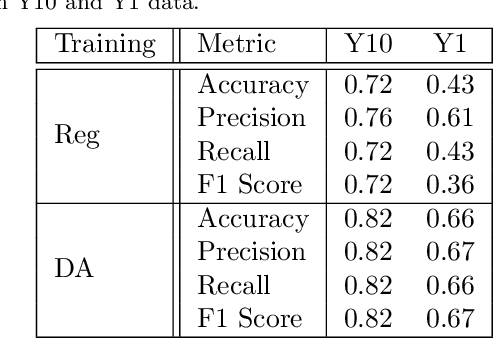
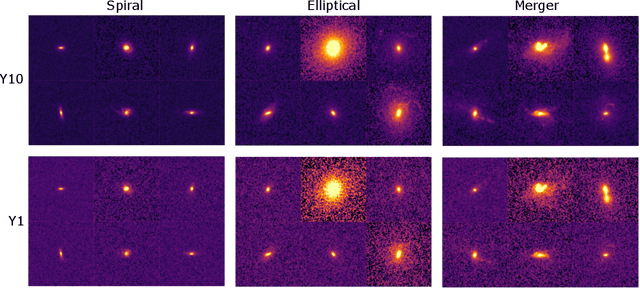
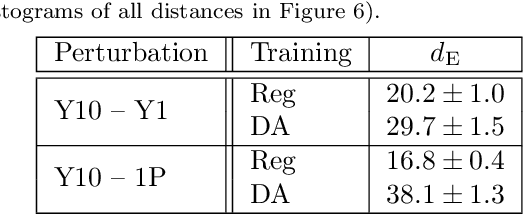
Abstract:Data processing and analysis pipelines in cosmological survey experiments introduce data perturbations that can significantly degrade the performance of deep learning-based models. Given the increased adoption of supervised deep learning methods for processing and analysis of cosmological survey data, the assessment of data perturbation effects and the development of methods that increase model robustness are increasingly important. In the context of morphological classification of galaxies, we study the effects of perturbations in imaging data. In particular, we examine the consequences of using neural networks when training on baseline data and testing on perturbed data. We consider perturbations associated with two primary sources: 1) increased observational noise as represented by higher levels of Poisson noise and 2) data processing noise incurred by steps such as image compression or telescope errors as represented by one-pixel adversarial attacks. We also test the efficacy of domain adaptation techniques in mitigating the perturbation-driven errors. We use classification accuracy, latent space visualizations, and latent space distance to assess model robustness. Without domain adaptation, we find that processing pixel-level errors easily flip the classification into an incorrect class and that higher observational noise makes the model trained on low-noise data unable to classify galaxy morphologies. On the other hand, we show that training with domain adaptation improves model robustness and mitigates the effects of these perturbations, improving the classification accuracy by 23% on data with higher observational noise. Domain adaptation also increases by a factor of ~2.3 the latent space distance between the baseline and the incorrectly classified one-pixel perturbed image, making the model more robust to inadvertent perturbations.
UAV Path Planning for Optimal Coverage of Areas with Nonuniform Importance
Oct 19, 2021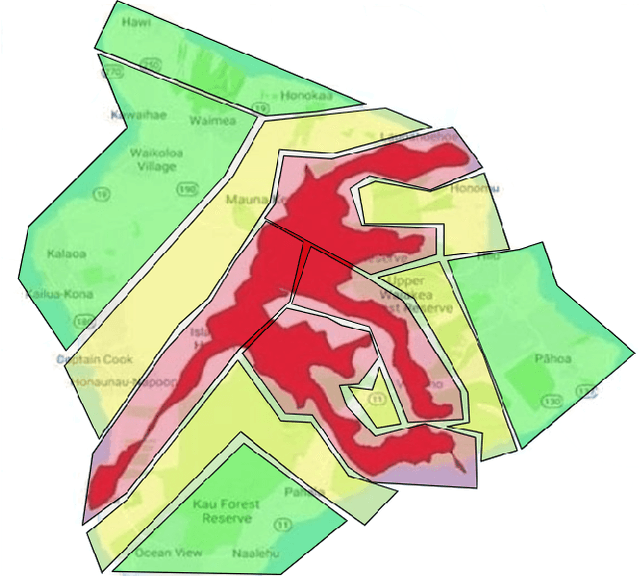
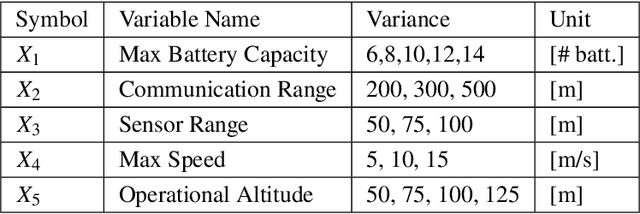
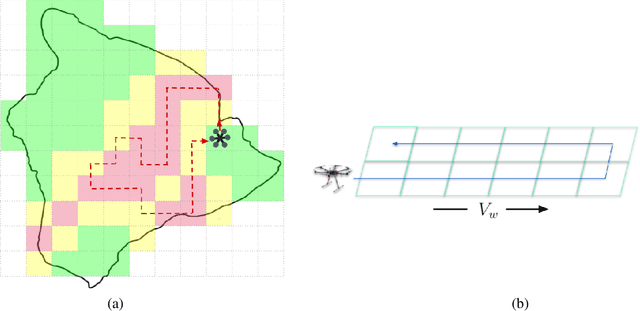
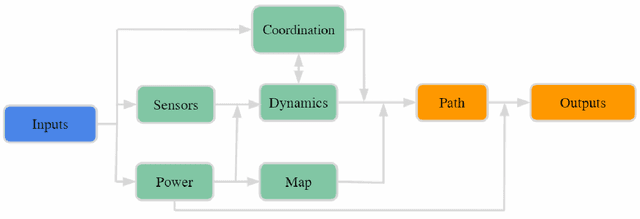
Abstract:Coverage of an inaccessible or difficult terrain with potential health and safety hazards, such as in a volcanic region, is difficult yet crucial from scientific and meteorological perspectives. Areas contained within this region can provide us with different types of valuable information of varying importance. We present an algorithm to optimally cover a volcanic region in Hawai`i with an unmanned aerial vehicle (UAV). The target region is assigned with a nonuniform coverage importance score distribution. For a specified battery capacity of the UAV, the optimization problem seeks the path that maximizes the total coverage area and the accumulated importance score while penalizing the revisiting of the same area. Trajectories are generated offline for the UAV based on the available power and coverage information map. The optimal trajectory minimizes the unspent battery power while enforcing that the UAV returns to its starting location. This multi-objective optimization problem is solved by using sequential quadratic programming. The details of the competitive optimization problem are discussed along with the analysis and simulation results to demonstrate the applicability of the proposed algorithm.
Dynamic Compressed Sensing of Unsteady Flows with a Mobile Robot
Oct 16, 2021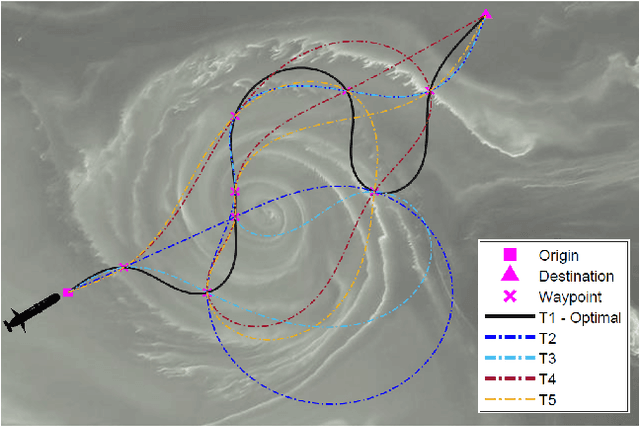
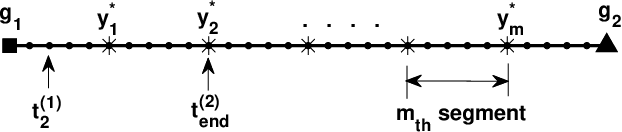
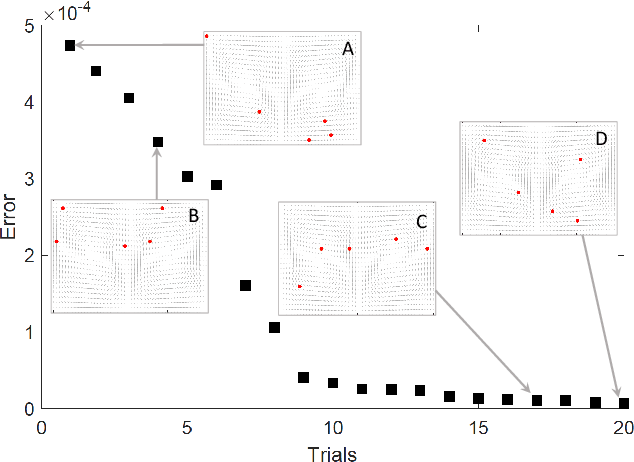
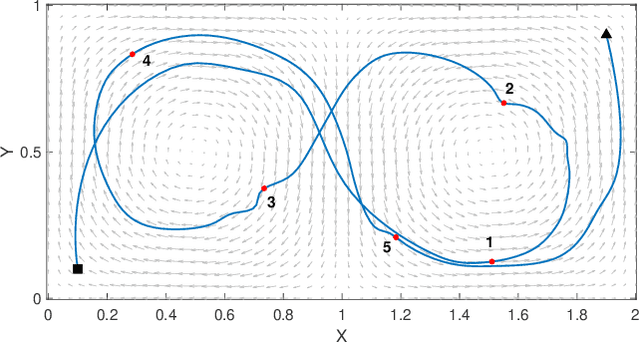
Abstract:Large-scale environmental sensing with a finite number of mobile sensor is a challenging task that requires a lot of resources and time. This is especially true when features in the environment are spatiotemporally changing with unknown or partially known dynamics. However, these dynamic features often evolve in a low-dimensional space, making it possible to capture their dynamics sufficiently well with only one or several properly planned mobile sensors. This paper investigates the problem of dynamic compressed sensing (DCS) of an unsteady flow field, which takes advantage of the inherently low dimensionality of the underlying flow dynamics to reduce number of waypoints for a mobile sensing robot. The optimal sensing waypoints are identified by an iterative compressed sensing algorithm that optimizes the flow reconstruction based on the proper orthogonal decomposition (POD) modes. An optimized robot trajectory is then found to traverse these waypoints while minimizing the energy consumption, time, and flow reconstruction error. Simulation results in an unsteady double-gyre flow field is presented to demonstrate the efficacy of the proposed algorithms. Experimental results with an indoor quadcopter are presented to show the feasibility of the resulting trajectory.
Koopman Operator Theory for Nonlinear Dynamic Modeling using Dynamic Mode Decomposition
Oct 16, 2021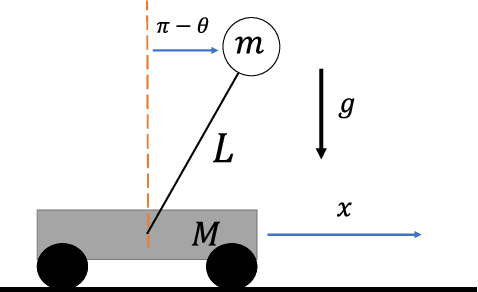
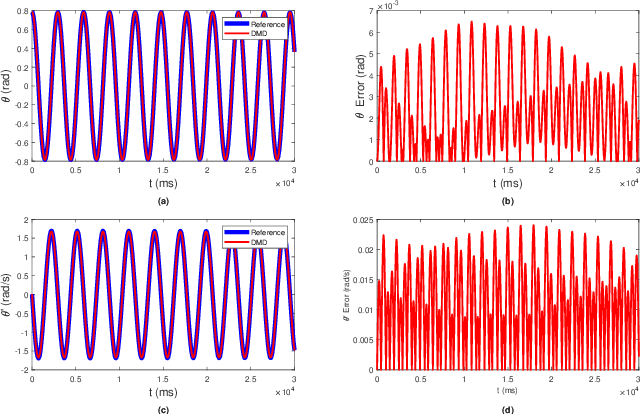
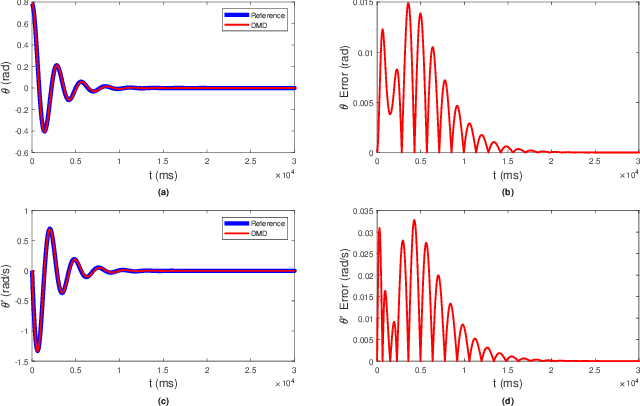
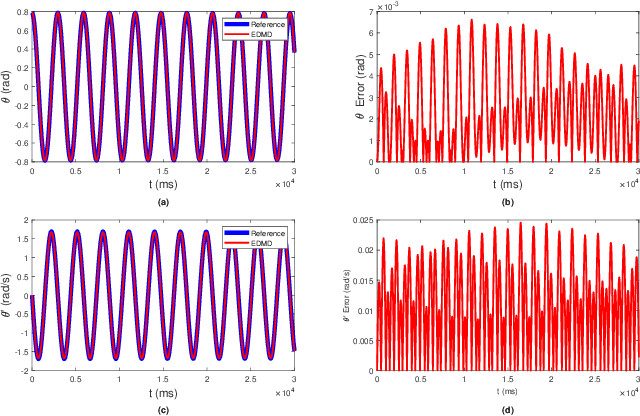
Abstract:The Koopman operator is a linear operator that describes the evolution of scalar observables (i.e., measurement functions of the states) in an infinitedimensional Hilbert space. This operator theoretic point of view lifts the dynamics of a finite-dimensional nonlinear system to an infinite-dimensional function space where the evolution of the original system becomes linear. In this paper, we provide a brief summary of the Koopman operator theorem for nonlinear dynamics modeling and focus on analyzing several data-driven implementations using dynamical mode decomposition (DMD) for autonomous and controlled canonical problems. We apply the extended dynamic mode decomposition (EDMD) to identify the leading Koopman eigenfunctions and approximate a finite-dimensional representation of the discovered linear dynamics. This allows us to apply linear control approaches towards nonlinear systems without linearization approximations around fixed points. We can then examine the fidelity of using a linear controller based on a Koopman operator approximated system on under-actuated systems with basic maneuvers. We demonstrate the effectiveness of this theory through numerical simulation on two classic dynamical systems are used to show DMD methods of evaluating and approximating the Koopman operator and its effectiveness at linearizing these systems.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge