Koopman Operator Theory for Nonlinear Dynamic Modeling using Dynamic Mode Decomposition
Paper and Code
Oct 16, 2021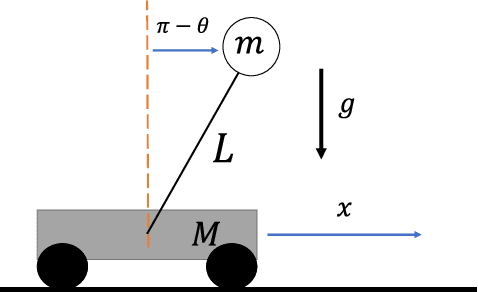
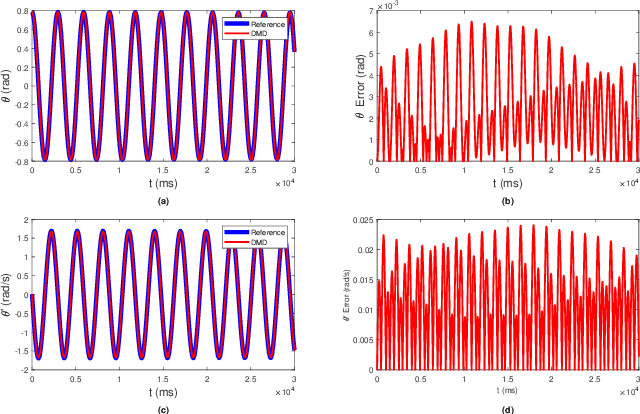
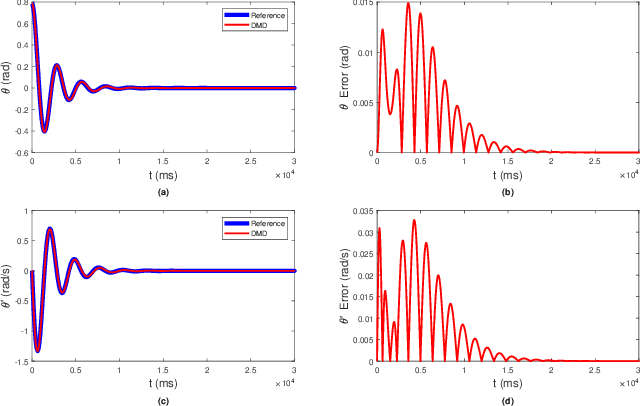
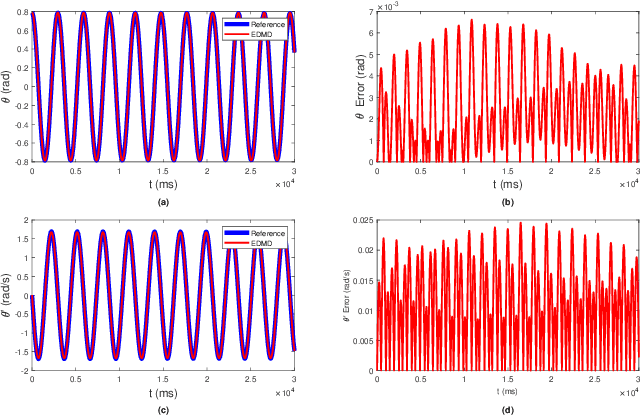
The Koopman operator is a linear operator that describes the evolution of scalar observables (i.e., measurement functions of the states) in an infinitedimensional Hilbert space. This operator theoretic point of view lifts the dynamics of a finite-dimensional nonlinear system to an infinite-dimensional function space where the evolution of the original system becomes linear. In this paper, we provide a brief summary of the Koopman operator theorem for nonlinear dynamics modeling and focus on analyzing several data-driven implementations using dynamical mode decomposition (DMD) for autonomous and controlled canonical problems. We apply the extended dynamic mode decomposition (EDMD) to identify the leading Koopman eigenfunctions and approximate a finite-dimensional representation of the discovered linear dynamics. This allows us to apply linear control approaches towards nonlinear systems without linearization approximations around fixed points. We can then examine the fidelity of using a linear controller based on a Koopman operator approximated system on under-actuated systems with basic maneuvers. We demonstrate the effectiveness of this theory through numerical simulation on two classic dynamical systems are used to show DMD methods of evaluating and approximating the Koopman operator and its effectiveness at linearizing these systems.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge