Adaptive Batch Sizes Using Non-Euclidean Gradient Noise Scales for Stochastic Sign and Spectral Descent

To maximize hardware utilization, modern machine learning systems typically employ large constant or manually tuned batch size schedules, relying on heuristics that are brittle and costly to tune. Existing adaptive strategies based on gradient noise scale (GNS) offer a principled alternative. However, their assumption of SGD's Euclidean geometry creates a fundamental mismatch with popular optimizers based on generalized norms, such as signSGD / Signum ($\ell_\infty$) and stochastic spectral descent (specSGD) / Muon ($\mathcal{S}_\infty$). In this work, we derive gradient noise scales for signSGD and specSGD that naturally emerge from the geometry of their respective dual norms. To practically estimate these non-Euclidean metrics, we propose an efficient variance estimation procedure that leverages the local mini-batch gradients on different ranks in distributed data-parallel systems. Our experiments demonstrate that adaptive batch size strategies using non-Euclidean GNS enable us to match the validation loss of constant-batch baselines while reducing training steps by up to 66% for Signum and Muon on a 160 million parameter Llama model.

Smoothing DiLoCo with Primal Averaging for Faster Training of LLMs

We propose Generalized Primal Averaging (GPA), an extension of Nesterov's method in its primal averaging formulation that addresses key limitations of recent averaging-based optimizers such as single-worker DiLoCo and Schedule-Free (SF) in the non-distributed setting. These two recent algorithmic approaches improve the performance of base optimizers, such as AdamW, through different iterate averaging strategies. Schedule-Free explicitly maintains a uniform average of past weights, while single-worker DiLoCo performs implicit averaging by periodically aggregating trajectories, called pseudo-gradients, to update the model parameters. However, single-worker DiLoCo's periodic averaging introduces a two-loop structure, increasing its memory requirements and number of hyperparameters. GPA overcomes these limitations by decoupling the interpolation constant in the primal averaging formulation of Nesterov. This decoupling enables GPA to smoothly average iterates at every step, generalizing and improving upon single-worker DiLoCo. Empirically, GPA consistently outperforms single-worker DiLoCo while removing the two-loop structure, simplifying hyperparameter tuning, and reducing its memory overhead to a single additional buffer. On the Llama-160M model, GPA provides a 24.22% speedup in terms of steps to reach the baseline (AdamW's) validation loss. Likewise, GPA achieves speedups of 12% and 27% on small and large batch setups, respectively, to attain AdamW's validation accuracy on the ImageNet ViT workload. Furthermore, we prove that for any base optimizer with regret bounded by $O(\sqrt{T})$, where $T$ is the number of iterations, GPA can match or exceed the convergence guarantee of the original optimizer, depending on the choice of interpolation constants.

A Distributed Data-Parallel PyTorch Implementation of the Distributed Shampoo Optimizer for Training Neural Networks At-Scale

Shampoo is an online and stochastic optimization algorithm belonging to the AdaGrad family of methods for training neural networks. It constructs a block-diagonal preconditioner where each block consists of a coarse Kronecker product approximation to full-matrix AdaGrad for each parameter of the neural network. In this work, we provide a complete description of the algorithm as well as the performance optimizations that our implementation leverages to train deep networks at-scale in PyTorch. Our implementation enables fast multi-GPU distributed data-parallel training by distributing the memory and computation associated with blocks of each parameter via PyTorch's DTensor data structure and performing an AllGather primitive on the computed search directions at each iteration. This major performance enhancement enables us to achieve at most a 10% performance reduction in per-step wall-clock time compared against standard diagonal-scaling-based adaptive gradient methods. We validate our implementation by performing an ablation study on training ImageNet ResNet50, demonstrating Shampoo's superiority over standard training recipes with minimal hyperparameter tuning.

Compositional Embeddings Using Complementary Partitions for Memory-Efficient Recommendation Systems

Modern deep learning-based recommendation systems exploit hundreds to thousands of different categorical features, each with millions of different categories ranging from clicks to posts. To respect the natural diversity within the categorical data, embeddings map each category to a unique dense representation within an embedded space. Since each categorical feature could take on as many as tens of millions of different possible categories, the embedding tables form the primary memory bottleneck during both training and inference. We propose a novel approach for reducing the embedding size in an end-to-end fashion by exploiting complementary partitions of the category set to produce a unique embedding vector for each category without explicit definition. By storing multiple smaller embedding tables based on each complementary partition and combining embeddings from each table, we define a unique embedding for each category at smaller cost. This approach may be interpreted as using a specific fixed codebook to ensure uniqueness of each category's representation. Our experimental results demonstrate the effectiveness of our approach over the hashing trick for reducing the size of the embedding tables in terms of model loss and accuracy, while retaining a similar reduction in the number of parameters.

Deep Learning Recommendation Model for Personalization and Recommendation Systems

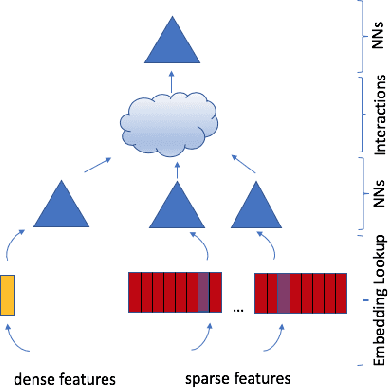
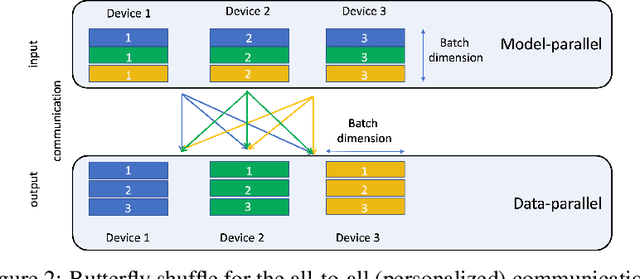
With the advent of deep learning, neural network-based recommendation models have emerged as an important tool for tackling personalization and recommendation tasks. These networks differ significantly from other deep learning networks due to their need to handle categorical features and are not well studied or understood. In this paper, we develop a state-of-the-art deep learning recommendation model (DLRM) and provide its implementation in both PyTorch and Caffe2 frameworks. In addition, we design a specialized parallelization scheme utilizing model parallelism on the embedding tables to mitigate memory constraints while exploiting data parallelism to scale-out compute from the fully-connected layers. We compare DLRM against existing recommendation models and characterize its performance on the Big Basin AI platform, demonstrating its usefulness as a benchmark for future algorithmic experimentation and system co-design.

A Progressive Batching L-BFGS Method for Machine Learning

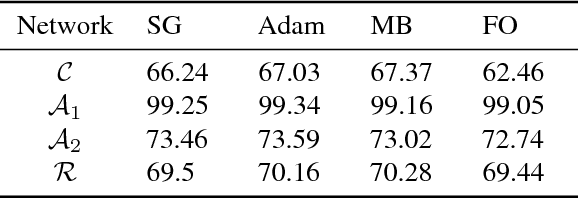
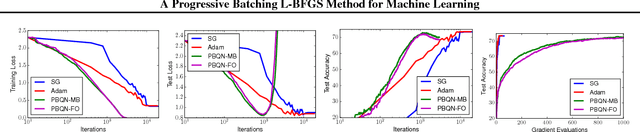
The standard L-BFGS method relies on gradient approximations that are not dominated by noise, so that search directions are descent directions, the line search is reliable, and quasi-Newton updating yields useful quadratic models of the objective function. All of this appears to call for a full batch approach, but since small batch sizes give rise to faster algorithms with better generalization properties, L-BFGS is currently not considered an algorithm of choice for large-scale machine learning applications. One need not, however, choose between the two extremes represented by the full batch or highly stochastic regimes, and may instead follow a progressive batching approach in which the sample size increases during the course of the optimization. In this paper, we present a new version of the L-BFGS algorithm that combines three basic components - progressive batching, a stochastic line search, and stable quasi-Newton updating - and that performs well on training logistic regression and deep neural networks. We provide supporting convergence theory for the method.

A Primer on Coordinate Descent Algorithms

This monograph presents a class of algorithms called coordinate descent algorithms for mathematicians, statisticians, and engineers outside the field of optimization. This particular class of algorithms has recently gained popularity due to their effectiveness in solving large-scale optimization problems in machine learning, compressed sensing, image processing, and computational statistics. Coordinate descent algorithms solve optimization problems by successively minimizing along each coordinate or coordinate hyperplane, which is ideal for parallelized and distributed computing. Avoiding detailed technicalities and proofs, this monograph gives relevant theory and examples for practitioners to effectively apply coordinate descent to modern problems in data science and engineering.

Practical Algorithms for Learning Near-Isometric Linear Embeddings

We propose two practical non-convex approaches for learning near-isometric, linear embeddings of finite sets of data points. Given a set of training points $\mathcal{X}$, we consider the secant set $S(\mathcal{X})$ that consists of all pairwise difference vectors of $\mathcal{X}$, normalized to lie on the unit sphere. The problem can be formulated as finding a symmetric and positive semi-definite matrix $\boldsymbol{\Psi}$ that preserves the norms of all the vectors in $S(\mathcal{X})$ up to a distortion parameter $\delta$. Motivated by non-negative matrix factorization, we reformulate our problem into a Frobenius norm minimization problem, which is solved by the Alternating Direction Method of Multipliers (ADMM) and develop an algorithm, FroMax. Another method solves for a projection matrix $\boldsymbol{\Psi}$ by minimizing the restricted isometry property (RIP) directly over the set of symmetric, postive semi-definite matrices. Applying ADMM and a Moreau decomposition on a proximal mapping, we develop another algorithm, NILE-Pro, for dimensionality reduction. FroMax is shown to converge faster for smaller $\delta$ while NILE-Pro converges faster for larger $\delta$. Both non-convex approaches are then empirically demonstrated to be more computationally efficient than prior convex approaches for a number of applications in machine learning and signal processing.