TeleRAG: Efficient Retrieval-Augmented Generation Inference with Lookahead Retrieval

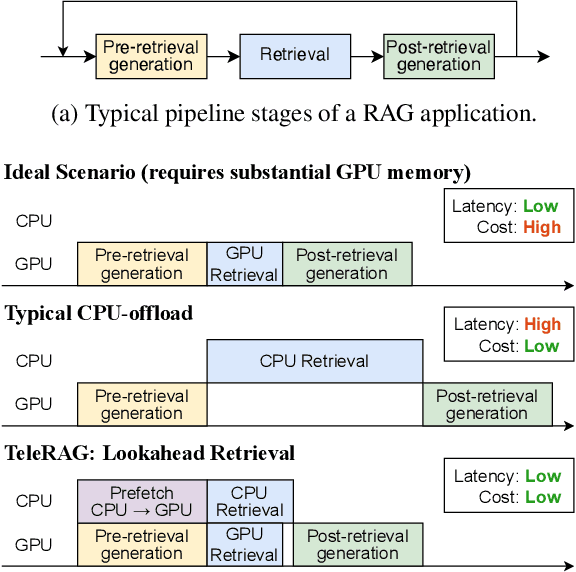
Retrieval-augmented generation (RAG) extends large language models (LLMs) with external data sources to enhance factual correctness and domain coverage. Modern RAG pipelines rely on large datastores, leading to system challenges in latency-sensitive deployments, especially when limited GPU memory is available. To address these challenges, we propose TeleRAG, an efficient inference system that reduces RAG latency with minimal GPU memory requirements. The core innovation of TeleRAG is lookahead retrieval, a prefetching mechanism that anticipates required data and transfers it from CPU to GPU in parallel with LLM generation. By leveraging the modularity of RAG pipelines, the inverted file index (IVF) search algorithm and similarities between queries, TeleRAG optimally overlaps data movement and computation. Experimental results show that TeleRAG reduces end-to-end RAG inference latency by up to 1.72x on average compared to state-of-the-art systems, enabling faster, more memory-efficient deployments of advanced RAG applications.

Tactic: Adaptive Sparse Attention with Clustering and Distribution Fitting for Long-Context LLMs

Long-context models are essential for many applications but face inefficiencies in loading large KV caches during decoding. Prior methods enforce fixed token budgets for sparse attention, assuming a set number of tokens can approximate full attention. However, these methods overlook variations in the importance of attention across heads, layers, and contexts. To address these limitations, we propose Tactic, a sparsity-adaptive and calibration-free sparse attention mechanism that dynamically selects tokens based on their cumulative attention scores rather than a fixed token budget. By setting a target fraction of total attention scores, Tactic ensures that token selection naturally adapts to variations in attention sparsity. To efficiently approximate this selection, Tactic leverages clustering-based sorting and distribution fitting, allowing it to accurately estimate token importance with minimal computational overhead. We show that Tactic outperforms existing sparse attention algorithms, achieving superior accuracy and up to 7.29x decode attention speedup. This improvement translates to an overall 1.58x end-to-end inference speedup, making Tactic a practical and effective solution for long-context LLM inference in accuracy-sensitive applications.

BlendServe: Optimizing Offline Inference for Auto-regressive Large Models with Resource-aware Batching

Offline batch inference, which leverages the flexibility of request batching to achieve higher throughput and lower costs, is becoming more popular for latency-insensitive applications. Meanwhile, recent progress in model capability and modality makes requests more diverse in compute and memory demands, creating unique opportunities for throughput improvement by resource overlapping. However, a request schedule that maximizes resource overlapping can conflict with the schedule that maximizes prefix sharing, a widely-used performance optimization, causing sub-optimal inference throughput. We present BlendServe, a system that maximizes resource utilization of offline batch inference by combining the benefits of resource overlapping and prefix sharing using a resource-aware prefix tree. BlendServe exploits the relaxed latency requirements in offline batch inference to reorder and overlap requests with varied resource demands while ensuring high prefix sharing. We evaluate BlendServe on a variety of synthetic multi-modal workloads and show that it provides up to $1.44\times$ throughput boost compared to widely-used industry standards, vLLM and SGLang.

Quest: Query-Aware Sparsity for Efficient Long-Context LLM Inference

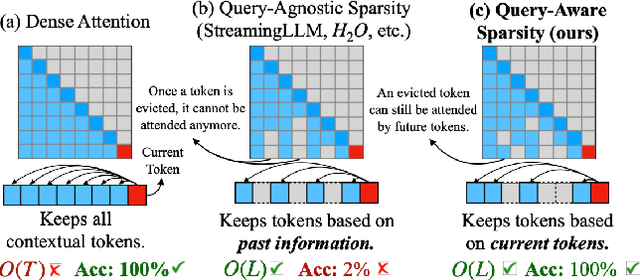
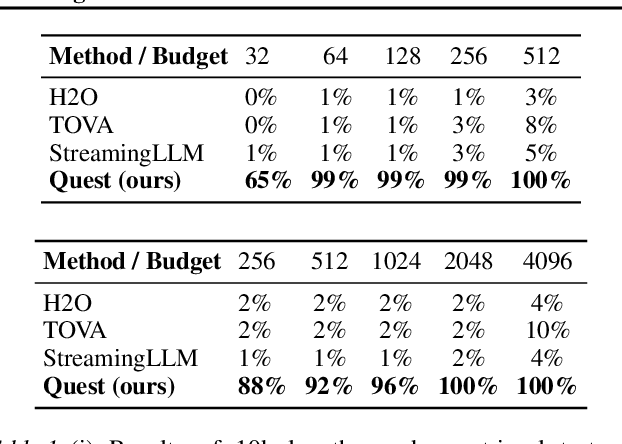
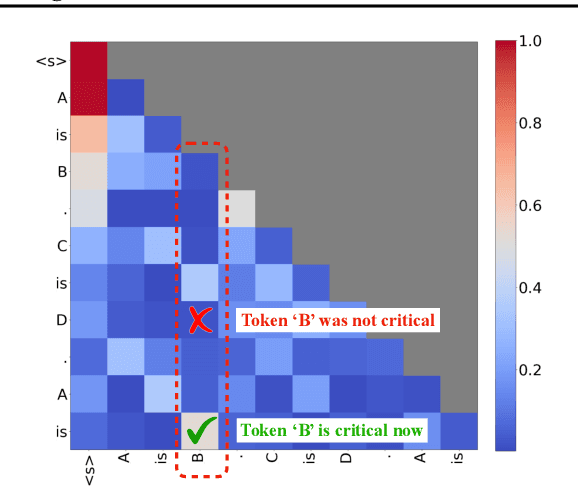
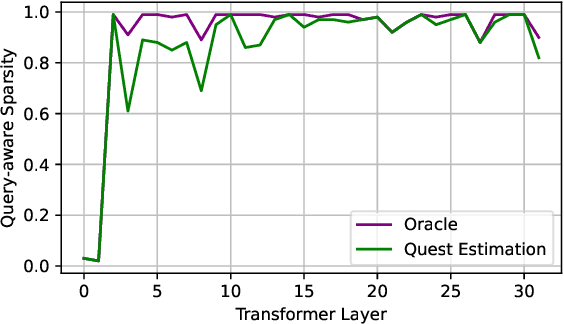
As the demand for long-context large language models (LLMs) increases, models with context windows of up to 128K or 1M tokens are becoming increasingly prevalent. However, long-context LLM inference is challenging since the inference speed decreases significantly as the sequence length grows. This slowdown is primarily caused by loading a large KV cache during self-attention. Previous works have shown that a small portion of critical tokens will dominate the attention outcomes. However, we observe the criticality of a token highly depends on the query. To this end, we propose Quest, a query-aware KV cache selection algorithm. Quest keeps track of the minimal and maximal Key values in KV cache pages and estimates the criticality of a given page using Query vectors. By only loading the Top-K critical KV cache pages for attention, Quest significantly speeds up self-attention without sacrificing accuracy. We show that Quest can achieve up to 2.23x self-attention speedup, which reduces inference latency by 7.03x while performing well on tasks with long dependencies with negligible accuracy loss. Code is available at http://github.com/mit-han-lab/Quest .

Fiddler: CPU-GPU Orchestration for Fast Inference of Mixture-of-Experts Models

Large Language Models (LLMs) based on Mixture-of-Experts (MoE) architecture are showing promising performance on various tasks. However, running them on resource-constrained settings, where GPU memory resources are not abundant, is challenging due to huge model sizes. Existing systems that offload model weights to CPU memory suffer from the significant overhead of frequently moving data between CPU and GPU. In this paper, we propose Fiddler, a resource-efficient inference engine with CPU-GPU orchestration for MoE models. The key idea of Fiddler is to use the computation ability of the CPU to minimize the data movement between the CPU and GPU. Our evaluation shows that Fiddler can run the uncompressed Mixtral-8x7B model, which exceeds 90GB in parameters, to generate over $3$ tokens per second on a single GPU with 24GB memory, showing an order of magnitude improvement over existing methods. The code of Fiddler is publicly available at \url{https://github.com/efeslab/fiddler}

Atom: Low-bit Quantization for Efficient and Accurate LLM Serving

The growing demand for Large Language Models (LLMs) in applications such as content generation, intelligent chatbots, and sentiment analysis poses considerable challenges for LLM service providers. To efficiently use GPU resources and boost throughput, batching multiple requests has emerged as a popular paradigm; to further speed up batching, LLM quantization techniques reduce memory consumption and increase computing capacity. However, prevalent quantization schemes (e.g., 8-bit weight-activation quantization) cannot fully leverage the capabilities of modern GPUs, such as 4-bit integer operators, resulting in sub-optimal performance. To maximize LLMs' serving throughput, we introduce Atom, a low-bit quantization method that achieves high throughput improvements with negligible accuracy loss. Atom significantly boosts serving throughput by using low-bit operators and considerably reduces memory consumption via low-bit quantization. It attains high accuracy by applying a novel mixed-precision and fine-grained quantization process. We evaluate Atom on 4-bit weight-activation quantization setups in the serving context. Atom improves end-to-end throughput by up to $7.73\times$ compared to the FP16 and by $2.53\times$ compared to INT8 quantization, while maintaining the same latency target.

Practical Algorithms for Learning Near-Isometric Linear Embeddings

We propose two practical non-convex approaches for learning near-isometric, linear embeddings of finite sets of data points. Given a set of training points $\mathcal{X}$, we consider the secant set $S(\mathcal{X})$ that consists of all pairwise difference vectors of $\mathcal{X}$, normalized to lie on the unit sphere. The problem can be formulated as finding a symmetric and positive semi-definite matrix $\boldsymbol{\Psi}$ that preserves the norms of all the vectors in $S(\mathcal{X})$ up to a distortion parameter $\delta$. Motivated by non-negative matrix factorization, we reformulate our problem into a Frobenius norm minimization problem, which is solved by the Alternating Direction Method of Multipliers (ADMM) and develop an algorithm, FroMax. Another method solves for a projection matrix $\boldsymbol{\Psi}$ by minimizing the restricted isometry property (RIP) directly over the set of symmetric, postive semi-definite matrices. Applying ADMM and a Moreau decomposition on a proximal mapping, we develop another algorithm, NILE-Pro, for dimensionality reduction. FroMax is shown to converge faster for smaller $\delta$ while NILE-Pro converges faster for larger $\delta$. Both non-convex approaches are then empirically demonstrated to be more computationally efficient than prior convex approaches for a number of applications in machine learning and signal processing.